Избранное трейдера _sg_
Кто хочет заработать?
- 17 февраля 2021, 21:51
- |
Устроим флэш-моб?
Я тут малость заработал сегодня на шортах и хочу, чтобы весь смартлаб тоже сказочно обогатился:
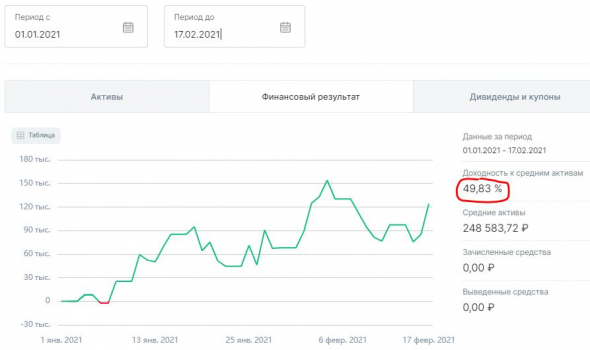
Предложение по заработку следующее: Мартын устроил конкурс, где бросил вызов, мол, его нужно переплюнуть, платит за это 20 000 руб.
Сейчас его топик набрал всего 373 плюсега:

( Читать дальше )
- комментировать
- ★105
- Комментарии ( 237 )
Читал Аллирога, много думал
- 17 февраля 2021, 13:49
- |
Прочитал не сегодня, так что вроде мысли улеглись.
Мне кажется, много внимания уделено философским вещам, с которыми я и так согласен. С другой стороны есть вопросы прикладного характера, на которые я ответов не вижу.
Рынок непредсказуем, ок.
Плечи и шорты многократно увеличивают риск слить депо, ок.
Главный способ слить деньги на рынке — выставлять стоп-лоссы.
ну-у, тут вроде как не так всё однозначно, но ладно — чтобы не застревать на этом, ок.
Как-бэ вокруг этих тезисов 80% текста крутится.
Принципы «торговли временем» -
- покупать нормальных эмитентов без плечей и только вверх,
- закрывать сделки только в плюс,
- делать разумную диверсификацию, чтобы не залипать надолго, пересиживая убытки.
( Читать дальше )
Ранние торги на Мосбирже с 1 марта - подробности
- 15 февраля 2021, 11:36
- |
С 1 марта планируем сдвинуть время начала торгов на срочном и валютном рынке, а также рынке драгметаллов на 7:00 утра (мск). На фондовом рынке все останется без изменений.
Теперь у вас появится возможность более оперативно реагировать на динамику нефтяных котировок, золота, валют и других инструментов, которые торгуются на мировых биржах почти круглосуточно. А трейдеры из восточных регионов смогут совершать сделки в удобное для них время.
Ну что, вы рады раннему старту или не очень? Запасаемся кофе? Напишите в комментариях свои мысли.

Пробуем "умный" стоп-лосс
- 11 февраля 2021, 15:09
- |
Сегодня темой нашей очередной статьи будет пример попытки улучшения своей доходности, при торговле по тренду.
Начальный алгоритм достаточно прост и стандартен — хай/лоу с периодом в 2000 баров. Тикер РТС Фьючерс. Специально был взят отрезок из прошлого, так как на нем он лучше всего «летал».
Параметр не подогнанный — начальный период в блоках TSLab обычно 20 и мы приписали пару нулей для увеличения продолжительности сделки.
Эквити в начальном виде.

Результаты показывать не будем, так как они будут более интересными, чем график дохода. Рекомендуем посмотреть как это работает на практике лично, если вы уже пользователь нашей программы)
Да — это не плохой график, но попытаемся сделать лучше! Выводим следующую формулу — открываем позицию, считаем доход/количество удерживаемых баров. Если значение растет, — значит рынок двигается с хорошей скоростью в нашу сторону. Если же начинает медленно падать или уходит в минус — значит перестал двигаться в нужном направлении. Пользуясь таким методом, алгоритм приближает стоп-лосс на 1 шаг цены с каждым баром. Для заметки: если работаете с историческими данными, то перепроверьте какой шаг цены вы указали. Иначе рискуете искать долго причину почему стоп не двигается ближе, как это было у меня!)
( Читать дальше )
Физико-математические основы Грааля. Часть 7
- 11 февраля 2021, 12:27
- |
Иногда они терзают душу, заставляют остановиться. Поток времени замедляется. Люди и события из прошлого оказываются рядом с тобой и ты испытываешь сомнения… Все ли правильно я сделал тогда? А сейчас? Ведь прошлое всегда накладывает свой отпечаток на настоящее и будущее.
Нет ответа...
Веду торговлю при помощи собственной ТС, которую достаточно долго и нудно разрабатывал. Есть периоды с отличной доходностью, есть убытки. Все как у всех. Нет главного — нет Грааля!
А ведь, когда-то давно, Колдун скинул мне Грааль. Как обычно — в виде рисунка.
Вот он:
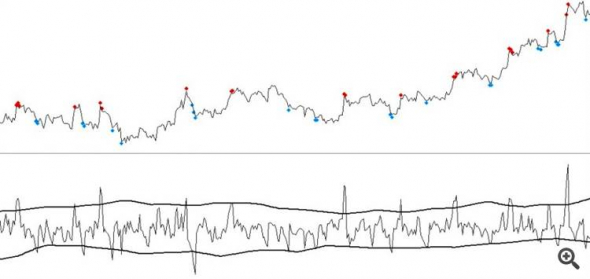
На вопрос — могу ли я использовать Его для обсуждения на форумах со страждущими, был получен еще более краткий ответ:

( Читать дальше )
Как реализуется неограниченный риск в опционах.
- 10 февраля 2021, 13:35
- |
1-покупка опциона
2-продажа опциона покрытого БА
3-продажа непокрытого опциона
Если вы купили опцион, то вы купили право на сделку в будущем с БА, заплатив за это право премию продавцу опциона. Вы можете реализовать это право или отказаться от него и ваши потери ограничены уплаченной премией.
Если вы продали покрытый опцион, то у вас есть обязанность поставить БА (для колла) или выкупить БА (для пута). В этом случае вы всегда выполняете свою обязанность и неограниченные потери вам не грозят.
Хуже если вы продали непокрытый опцион. Продавая непокрытый опцион, вы планируете выкупить опцион в критический момент и, если опционный стакан пустой, вы рассчитываете на сделку с БА, делая непокрытый опцион покрытым. Но здесь вас может ждать жесткий облом. Биржа задирает ГО на проданный опцион и на БА и у вас просто не хватает денег на сделку с БА. Всё. Вы приплыли. Добро пожаловать в пустой опционный стакан покупать по бешеной цене или за вас это сделает брокер.
Так реализуется неограниченный риск в опционах.
Парный трейдинг не для всех
- 10 февраля 2021, 12:55
- |
Я предлагаю взглянуть на с другой стороны и торговать корзину из более чем 200 акций (да, извините, но это не для российского рынка — даже 20-30 акций недостаточно). Для начала нужно высчитать синтетик у которого будет минимальная дисперсия — всех интересующихся отсылаю к трудам hrenfx, который, впрочем, пошел путем непрозрачных и требовательных вычислений, которые требуют большое кол-во памяти и не в состоянии рассчитать синтетик для более чем 30 и более инструментов. Каждый желающий прочитав посты hrenfx может самостоятельно все вычислить используя несколько строк на Python. Чтобы не утомлять деталями в финале получим синтетик вида k1*msft + k1*aapl +… k_n*XLNX. Одна часть синтетика будет с положительными значениями, другая с отрицательными. Это и будет синтетик с минимальной дисперсией, который вы уже можете начать торговать. В реальности нужно будет нормировать коэффициенты и отсеять акции вес которых в портфеле, например, меньше 5-10% (все зависит от торгуемого капитала — ведь нужно будет на эти 5% купить минимальное кол-во акций). Так же можно убрать и дорогие акции AMZN, TESLA etc… Разумно выбрать одну часть синтетика с отрицательными или положительными коэффициентами и торговать «one leg» по оценке на основе полного синтетика. Это снизит издержки и повысит вашу прибыль.
( Читать дальше )
Наш мозг в эпоху катаклизмов. Часть 2. Почему мозг за нас решает? Мозг во сне, гипнозе и в стрессе. триединый мозг. Прокрастинация. Как научиться принимать правильные решения?
- 10 февраля 2021, 09:04
- |
Завершу рассказ о книге Наш мозг в эпоху катаклизмов.
Электронная книга https://t.me/kudaidem/1864
( Читать дальше )
Сохранённый архив ордерлогов с ftp.zerich.com доступен по новому адресу в течение 2 недель
- 09 февраля 2021, 17:54
- |
Итак, весь архив доступен по адресу: ftp://eugene:12345678@212.24.104.175
На текущий момент там осталось 1.7 TB лимита трафика, после исчерпания которого провайдер сервиса ограничит скорость в 10 раз (до 10 мегабит/с). Так что на высокой скорости полный архив смогут скачать ~9 человек. Сервер проработает 2 недели.
Касаемо дальнейших перспектив сбора и хранения ордерлогов:
Насколько я понимаю — это была инициатива «Церих», у них там был какой-то отдел развития алготрейдинга. Верников делал об этом интервью. Если у кого-то есть какие-то идеи/выход на подобных людей, то со своей стороны могу бесплатно написать ПО, которое будет записывать ордерлоги в формате qsh (или в более адекватном).
Наш мозг в эпоху катаклизмов. Мозг и сахар. Мозг и Алкоголь. Мозг и движение. Плацебо.
- 09 февраля 2021, 09:32
- |
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал
