Продолжение. Предыдущая серия:
Мои итоги 2017

Долго слоупочил, но наконец-то хватило терпения подвести результаты за прошедший год. Если коротко — год по понятным причинам был сложный, в убытках оказалась рекордная доля активов за несколько десятилетий, а поскольку системы у меня только инвестиционные (все-таки, основной доход у меня от работы, и это наверное долго, а может и всегда будет так, а торговля — 2 часа в месяц баловства для) — то они не могут зарабатывать когда все сливает.

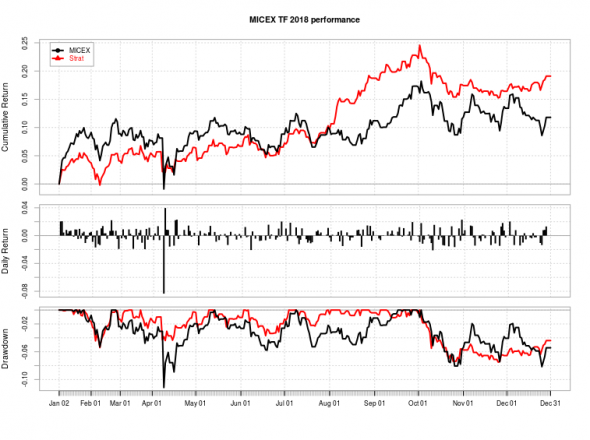
Начнем с хорошего — т.е. российского рынка. Тут результаты в принципе неплохие и почти догнали ожидания за год:
Ретурн +19.1% годовых c максимальной просадкой 7.5% и Шарпом 1.6. Последние 3 месяца года, конечно, подкачали, и весна прошла во флэте, но по итогу результат достойный и обгоняет индекс ММВБ (индекс ММВБ полной доходности «нетто»: ретурн 18.2% годовых с максимальной просадкой 11.1%) — немного по доходности и существенно — по максимальной просадке (спасибо А.Г. за данные по полной доходности)

( Читать дальше )

Суть проблемы:



Обнуленное НКД вернули 11.12.18

Скрин ссылок:



( Читать дальше )

По мотивам такого же поста по МРСК ЦП, прикинул, что же ждет нас в МРСК Волги по дивидендам.
Финплан:


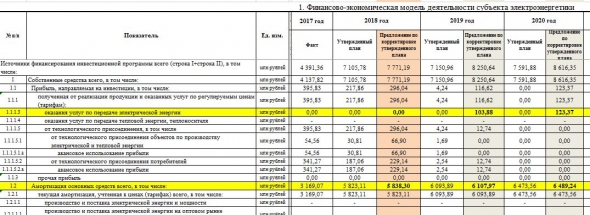
Составил табличку по данным последнего финплана и по моему прогнозу по чистой прибыли и амортизации а также формуле из дивполитики:


( Читать дальше )

7 декабря опубликовали измененный финплан МРСК ЦП.
Я решил изучить его на предмет будущего компании, на год-два впред.
Прогнозы чистой прибыли по годам тут смотреть смысла нет, т.к. они постоянно сильно занижаются, а вот параметры финансирования инвестпрограммы — это то, что более менее кореллирует с реальностью и на что можно опереться в оценках.

Для этого посмотрим, что же запланировано в отчислениях на инвестпрограмму с прибыли, полученной от передачи ЭЭ, а также какое финансирование запланировано с амортизации
(все расчеты по прибыли и амортизации и дивидендам — буду делать по данным МСФО).

Итак, вот таблица из финплана, где обозначены источники финансирования инвестпрограммы:



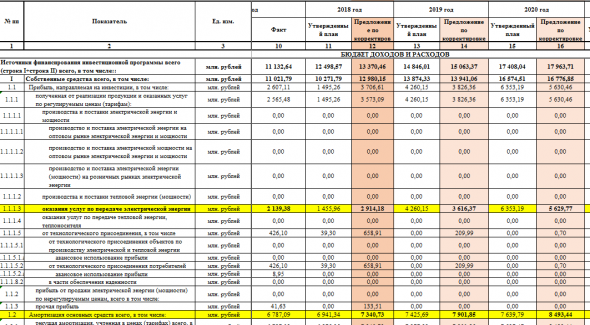
Тут мы видим, такие цифры:
Год   Отчисления от передачи ЭЭ    Отчисления с амортизации
2018г      2914,18 млн                      7340,73

( Читать дальше )

 

 3. Оправдано ли использование логарифмического нормального распределения для описания терминального состояния базового актива

Можно догадаться, почему именно логнормальную модель распределения использовали Блэк и Шолес при решении задачи о нахождении справедливой стоимости опциона. Модель с гауссовыми приращениями брать было нельзя – она допускает уход цены БА в отрицательную область. Следующая, относительно простая логнормальная модель вполне годилась. Найденное на ее основе решение стало основой всей современной теории опционов.

Теперь ложка дегтя.

Мы предполагаем, что приращения цен акций, входящих в расчет индекса РТС, независимы и подчинены закону логарифмического нормального распределения. Поэтому при вычислении цен опционов на эти акции мы используем формулы БШ.

Но, согласно Центральной предельной теореме, из этого же предположения следует и то, что  распределение приращений их линейной комбинации (то есть самого индекса РТС) должно быть близким к нормальному,  тогда для расчета стоимости опционов на индекс РТС правильнее использовать формулу Башелье. Тем не менее, мы используем формулу БШ. Видимо, в расчете на то, что кривая волатильности все исправит.

( Читать дальше )

Тестирование стохастического осциллятора на исторических данных

          В данной статье нас интересует возможность проверить на исторических данных эффективность использования стохастического осциллятора для прогнозирования будущего движения цены. Данный индикатор технического анализа показывает положение текущей цены относительно диапазона цен за определенный период в прошлом и измеряется в процентах.  Чтобы рассчитать значение стохастического осциллятора можно воспользоваться следующей формулой: K = (C – L_min)/(H_max-L_min)*100,

         где С – цена сегодняшнего закрытия,

         L_min – минимальная цена за расчетный период,

         H_max — максимальная цена за расчетный период.

         В качестве расчетного периода будем использовать период равный 5 дням. При этом считается, что стохастический осциллятор дает сигнал на покупку когда K был < 20%, а потом повысился и стал больше 20%, а сигнал на продажу данный индикатор дает тогда, когда K был > 80%, а потом понизился и стал меньше 80%.

( Читать дальше )

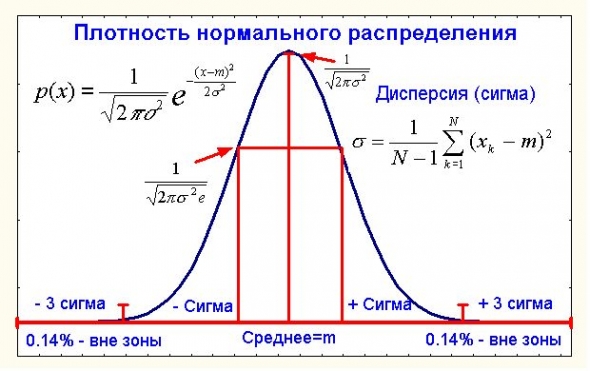
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

 
 

А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x

( Читать дальше )

Есть двое. Назовем их I и II. У каждого по десять рублей. Эта симметричная парочка играет в игру. Они берут симметричную 50/50 монетку и кидают ее. Если орел--то I отбирает у II один рубль. Если решка--то II отбирает у I один рубль. Монетку они кидают много-много раз, они терпеливые. Кто выиграет?

В моем понимании задача имеет самое непосредственное отношение к рынку.

UPD 17:36  Задача простая, в комментах накопилось некое общее вью. Так что нечего тут интригу тянуть. Рад, что уровень смартлаба неплох. Когда эту задачу в научной среде задаешь, там все хуже :) Правда, там на подумать времени нет.

Ответ--кто-то выиграет. Причем этот ответ не зависит от начального количества бабла у игроков, хоть по миллиону--все равно кто-то выиграет. Многие отвечают что не выиграет никто--но это неверно. Лично меня поражает то, что такой примитив тем не менее многое объясняет на бирже и в жизни. Вся эволюция так и устроена--бросается монетка, кому-то везет, кому-то нет. Кто до нуля добрался--все, отыгрался. А кто-то перешел на следующий уровень. Но кто-то обязательно занулится, а кто-то вылезет в люди. И никакого объяснения этому зачастую просто нет, монетка так легла. 

Конечно, в жизни среднее не нулевое, как в этой задаче. Но если среднее много меньше ско, то на небольших временах будет похоже. 

Всем привет!

Сбор участников завершён!

Напомню, что мы искали лучших из лучших трейдеров со смартлаба, имеюших высшее образование и готовых сразиться на еженедельках Ri/Si, чтобы отстоять честь своей альма-матер.

Итак, со всего смартлаба нас набралось ровно 10:

1. KiboR (Бауманка)
2. Лоссбой (МИФИ)
3. К.О'Тяра (МФТИ)
4. Sergey Pavlov (СФУ)
5. Борис Боос (НУ Узбекистана)
6. Стас Бржозовский и ch5oh (СПбГУ)
7. Lis' (ГУУ)
8. Александр (ЮРГТУ (НПИ))
9. Андрей (СГТУ)
10. Дон Маттео (ДГТУ)
--------------------------------------------------------------------------

Условия конкурса:

1. Старт: 35 000 руб
2. Период (15 недель): с 17.09.2018 по 30.12.2018
3. Инструмент: еженедельки RI/Si
4. Мин.количество риска в неделю: 10% от депо
5. Подбивать ежедневно свой результат в общую таблицу гуглщит: да
6. Отправлять еженедельно скрин эквити из лк брокера для общего контроля: да
7. Возможность ДХ фьючом (для тех, кому она позарез нужна): да

( Читать дальше )