Роботы

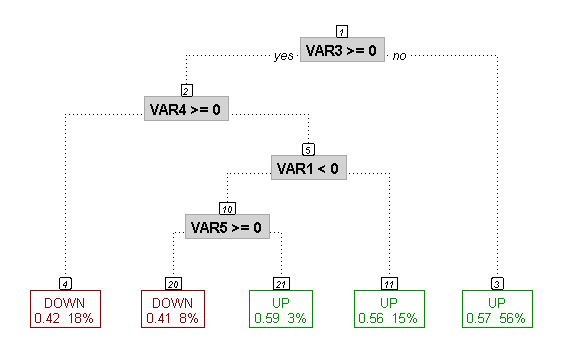
Интересный подход к предсказанию направления  рынка рассмотрен в статье "Using CART for Stock Market Forecasting". Для того, чтобы предугадать движение цены на недельном отрезке используется техника под названием CART (Classification And Regression Trees) — построение классификационного графа (дерева) с целью предсказать значение  целевой характеристики (цены) на основании набора объясняющих переменных. CART находит применение во многих областях науки и техники, но применим и в торговле, так как обладает набором свойств, хорошо подходящими для этой цели:

• может применяться при любом типе статистического распределения
• может применяться как для линейных, так и нелинейных зависимостей
• устойчив к событиям, выходящим за рамки статистических распределений

Для построения дерева автор использует библиотеку языка R, вычисляющую рекурсивное разделение (Recursive Partitioning) rpart.

( Читать дальше )

В компьютерных стратегических играх и шахматах лучше играет тот, кто владеет не только качественной реализацией одной стратегии, но владеет еще и набором стратегий, которые он по ходу игры может подбирать к данному сопернику.

Кто совсем не диверсифицирует свой портфель, тот может нарваться на черного лебедя и потерять большую долю портфеля. Вроде входа ставки ЦБ, кризиса 2008 года или шипа на тонком рынке — одномоментной потери ликвидности. 

Многие диверсифицируют только активы. Скажем, спекулируют сразу 2-4 фьючерсами, а не 1. Или инвестируют сразу в 40 акций, а не в 1. Это их спасает иногда. Но не всегда. 

Я думаю, существует три уровня возможной диверсификации: 
1. По активам
2. По стратегиям
3. По денежному потоку

Про диверсификацию по активам знают все — не храни все в одной корзине.

Для объяснения диверсификации по стратегиям приведу свои стратегии. 

Мои текущие торговые стратегии: 
1. Инвестиционная — дорого продавать и дешево покупать. На акциях. 
2. Спекулятивная — покупать то, что растет, чтобы продать еще дороже. Продавать то, что падает, чтобы купить еще дешевле. На фьючерсах на индекс РТС и курс доллара. 
3. Ребалансировка — мы не знаем будущего, поэтому диверсифицируем портфель на 3 не связанные друг с другом компоненты (классы активов) и держим пропорцию. За счет этого, мы не так уязвимы к кризисам. 
4. Черный лебедь — ищем возможные шипы на тонких рынках и различные обвалы, которые могут происходить в дни экспирации опционов на фьючерсы, в дни выхода важной статистики, решений ФРС, ЦБ.

( Читать дальше )

На следующей неделе выложу расширенную версию.



Роботизация торговли/QUIK & MT5/ — [email protected]

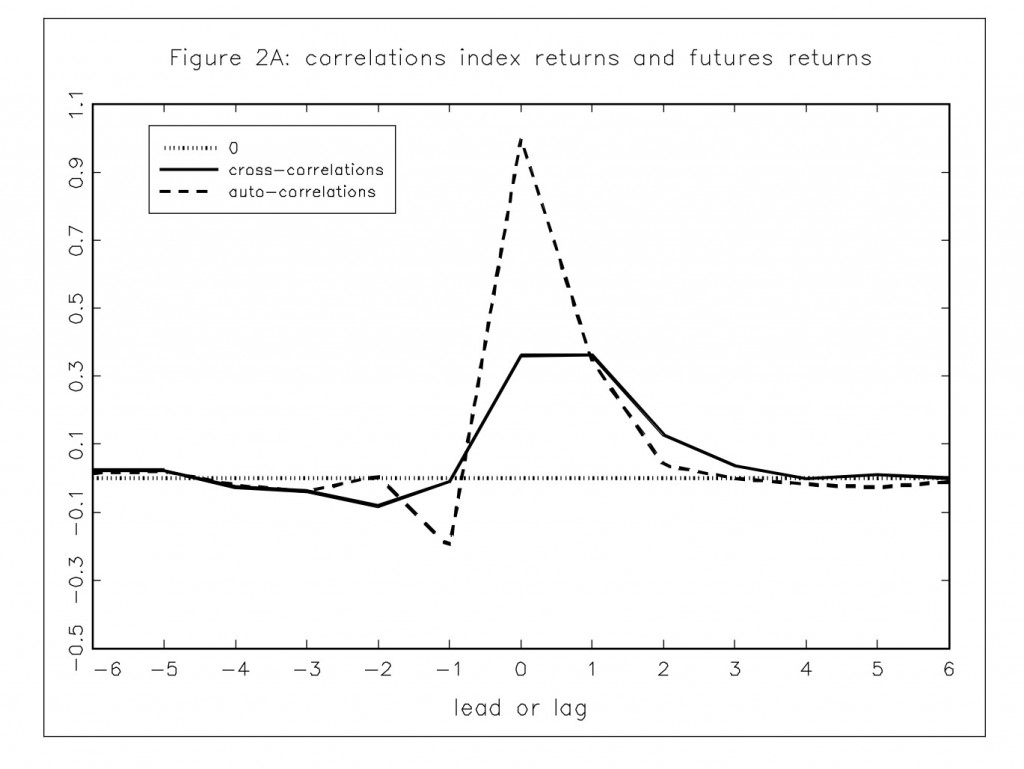
Трейдеры, которые приобрели мою программу robot_uralpro (см. пост на смарт-лабе), спрашивают, можно ли доработать алгоритм для применения его на современном рынке? Напомню, стратегия робота основана на взаимоотношении цен синтетического индекса, составляемого динамически из рыночных цен акций, входящих в индекс РТС, и фьючерса RI. Идея «одноногого» статистического арбитража, реализованного в роботе, будет работать и сейчас, только в том случае, если научиться правильно определять, какой актив опережает другой в смысле динамики их цен. Эта статья посвящена правильному выявлению такого взаимодействия, которое в англоязычных источниках называется «lead-lag relationship» -опережение-отставание между разными активами.

Те алготрейдеры, кто не приобретал robot_uralpro, тоже сочтут эту статью полезной, так как lead-lag relationship может использоваться в стратегиях парного трейдинга и им подобным. Например, определив такое взаимодействие, можно исключить из парного трейдинга один из активов ( с учетом того, конечно, что отношение торгуемых инструментов было описано четкой моделью) и значительно увеличить тем самым прибыльность стратегии.

( Читать дальше )

Разработаю торговую систему на заказ, алготрейдинг, любой брокер

Вот тут smart-lab.ru/blog/248375.php Трейдер² наехал на Костю Гармалыгу, на мой взгляд, безосновательно.
Говорить о ничтожности стратегии можно, когда проведено полное и корректное бэк-тестирование на разных состояниях рынка.
А абстрактно сравнивать просадки без соотнесения с показателем риск/прибыль вообще нельзя.
Есть стратегии, которые берут 1000% прибыли на трейд. Но и вин/лосс у них соответственно, даже не 1 к 3.
Но на фига беспокоиться о слитом депозите, если, к примеру, на 5 слитых приходится один удесятиренный?
Всего лишь надо построить ММ чтобы дожить до такого удесятирения, и чтобы дисперсия не стерла со счета все средства.
Покупка очень дешевых опционов в расчете на очень редкое событие — один из примеров, но речь не об этом.

Речь о стейтментах (и результатах тестирования) которым можно верить.
Придумали стратегию, прогнали в тестере с учетом всех комиссий и проскальзываний, получили эквити:


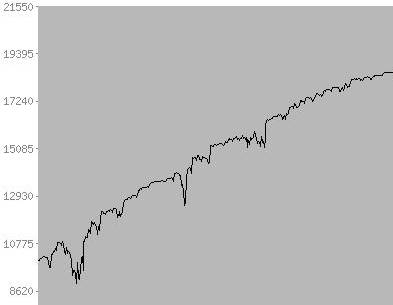
Период — полтора года, как я понимаю, по мнению многих — более чем достаточно.


( Читать дальше )

Продолжаем разбирать численное решение уравнения Хамильтона-Якоби-Беллмана. В прошлой части мы составили выражение для оператора 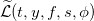, в котором есть слагаемые, получить значение которых можно из реальных данных. Во-первых, что из себя представляют дифференциальные матрицы D1,D2. Это матрицы размерностью 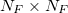, где, для D1(согласно определению в части 4) в ячейках [j,j] стоят -1, если fj<0 и 1 в остальных случаях,  в ячейках [j,j+1] стоят 1, если fj<0 и 0 в остальных случаях, и в ячейках [j,j-1] стоят -1, если fj≥0 и 0 — в остальных случаях. Как составить матрицу D2, я думаю, вы догадаетесь сами, взглянув на ее определение в

( Читать дальше )

Ребята, вот вы говорите роботы, hft и все такое. 

Но эти алгоритмы все анализируются, попадают в базы данных разработчиков софта, также есть риск что робот заглючит и будет лить депо либо на хвост роботу сядет кукл.

Либо этот алгорим станет известным и на нем начнут писать своих роботов уже разработчики софта и в итоге это все перестанет работать.

Вас волнуют эти проблемы? как вы их решаете?
 

Робот прошёл все тесты, и да мы его запустили на реальный счёт !

с 18-го числа наше детище заработало 60 % от начального депозита, гоняя всего 3 контракта по рынку ибо мы (не перечисленные ниже люди) нищеброды, ну ничего не поделаешь...

Отдельное спасибо !

Алексею Богатову (Ака доктор Богатов), моему учителю и ментору !!! http://smart-lab.ru/profile/Boggi/

Андрею Ерохину! Парень просто космос, оверинженер ! http://smart-lab.ru/profile/Doopler/

Саро Микаеляну! Человек не нуждается в представлении по определению !( кстати ждём релиза 2.0 ) http://smart-lab.ru/profile/Saro/

( Читать дальше )

Продолжаем разбирать работу JIANGMIN XU «Optimal Strategies of High Frequency Traders». Чтобы составить уравнение оптимального контроля, сначала сформулируем проблему оптимизации алгоритма при используемых стратегиях θ,  как достижение максимума следующего матожидания:

,

( Читать дальше )