SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
случайный процесс
Физико-математические основы Грааля. Часть 7
- 11 февраля 2021, 12:27
- |
Воспоминания...
Иногда они терзают душу, заставляют остановиться. Поток времени замедляется. Люди и события из прошлого оказываются рядом с тобой и ты испытываешь сомнения… Все ли правильно я сделал тогда? А сейчас? Ведь прошлое всегда накладывает свой отпечаток на настоящее и будущее.
Нет ответа...
Веду торговлю при помощи собственной ТС, которую достаточно долго и нудно разрабатывал. Есть периоды с отличной доходностью, есть убытки. Все как у всех. Нет главного — нет Грааля!
А ведь, когда-то давно, Колдун скинул мне Грааль. Как обычно — в виде рисунка.
Вот он:
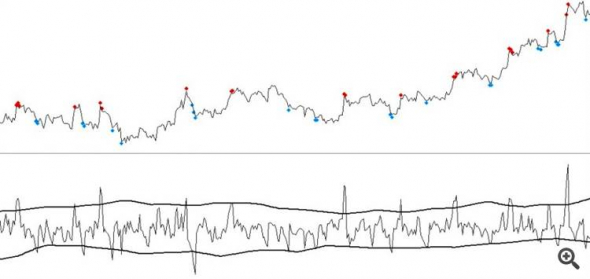
На вопрос — могу ли я использовать Его для обсуждения на форумах со страждущими, был получен еще более краткий ответ:

( Читать дальше )
Иногда они терзают душу, заставляют остановиться. Поток времени замедляется. Люди и события из прошлого оказываются рядом с тобой и ты испытываешь сомнения… Все ли правильно я сделал тогда? А сейчас? Ведь прошлое всегда накладывает свой отпечаток на настоящее и будущее.
Нет ответа...
Веду торговлю при помощи собственной ТС, которую достаточно долго и нудно разрабатывал. Есть периоды с отличной доходностью, есть убытки. Все как у всех. Нет главного — нет Грааля!
А ведь, когда-то давно, Колдун скинул мне Грааль. Как обычно — в виде рисунка.
Вот он:

На вопрос — могу ли я использовать Его для обсуждения на форумах со страждущими, был получен еще более краткий ответ:

( Читать дальше )
- комментировать
- ★8
- Комментарии ( 37 )
Борьба за Грааль. Итоги января 2021 г.
- 30 января 2021, 13:19
- |
Грааль...
У меня аж ручонки начинают трястись от одного этого слова.
Раз на рынке протекает немарковский случайный процесс, то, значит, Он есть. Его не может не быть...
МетОды изъятия наличных с рынка могут быть разными, но они не могут быть представлены в виде решения дифференциального уравнения для марковских процессов даже с учетом сноса (дрифта). Запомните это.
А раз тут принято публиковать отчеты о торговле, то и я туда же. Ибо негоже отставать от местных миллионеров.
Вуаля!
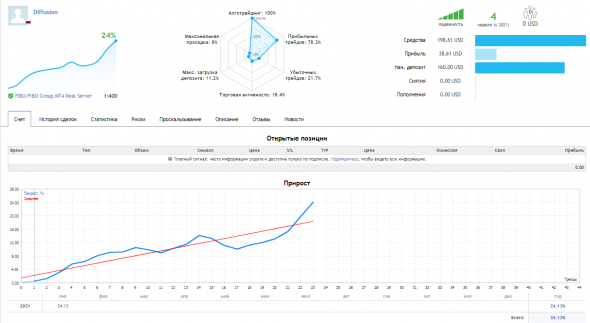
М-да....
До Грааля еще далеко, но жажда узреть Его неутолима.
До встречи, друзья мои.
Toddler.
У меня аж ручонки начинают трястись от одного этого слова.
Раз на рынке протекает немарковский случайный процесс, то, значит, Он есть. Его не может не быть...
МетОды изъятия наличных с рынка могут быть разными, но они не могут быть представлены в виде решения дифференциального уравнения для марковских процессов даже с учетом сноса (дрифта). Запомните это.
А раз тут принято публиковать отчеты о торговле, то и я туда же. Ибо негоже отставать от местных миллионеров.
Вуаля!

М-да....
До Грааля еще далеко, но жажда узреть Его неутолима.
До встречи, друзья мои.
Toddler.
Физико-математические основы Грааля. Часть 6
- 16 января 2021, 20:18
- |
Вечер добрый, господа!
Мы провели исследования (см. https://smart-lab.ru/blog/668918.php и https://smart-lab.ru/blog/669222.php), на основании которых можно сделать вывод, что на рынке мы имеем дело со случайным процессом, который не дает никаких преимуществ пред любыми метОдами.
Никто не может быть уверенным в том, что он всегда будет зарабатывать так же как сейчас. Несмотря на обилие миллионеров здесь на форуме. Вот так вот...
Добавим исследования.
1. Зависимость приращений от часа внутри суток:
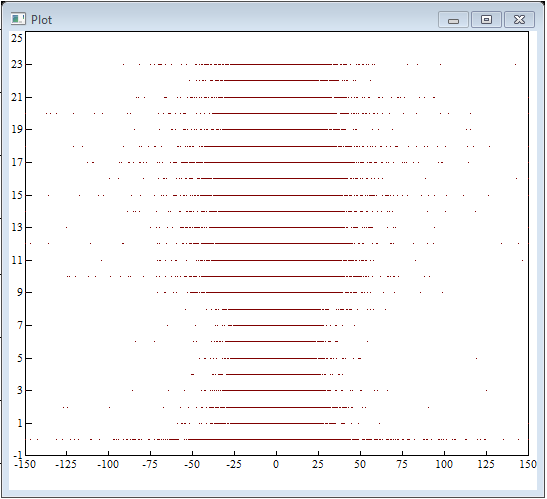
Очевидно, что, зависимость приращений от часа суток выражается только в нестационарности дисперсии процесса и не более того… А ведь условие получения Грааля состоит в некой асимметрии, как правильно заметил Великий Трейдер svgr.
2. Зависимость текущего приращения от предыдущего для стационарного ряда цен OPEN равнотиковых баров (получен одним из Волшебников для пары EURUSD за 2016-2017 гг. Получен он был на котировках Дукаскопи, по 100 тиков на 1 бар)
( Читать дальше )
Мы провели исследования (см. https://smart-lab.ru/blog/668918.php и https://smart-lab.ru/blog/669222.php), на основании которых можно сделать вывод, что на рынке мы имеем дело со случайным процессом, который не дает никаких преимуществ пред любыми метОдами.
Никто не может быть уверенным в том, что он всегда будет зарабатывать так же как сейчас. Несмотря на обилие миллионеров здесь на форуме. Вот так вот...
Добавим исследования.
1. Зависимость приращений от часа внутри суток:

Очевидно, что, зависимость приращений от часа суток выражается только в нестационарности дисперсии процесса и не более того… А ведь условие получения Грааля состоит в некой асимметрии, как правильно заметил Великий Трейдер svgr.
2. Зависимость текущего приращения от предыдущего для стационарного ряда цен OPEN равнотиковых баров (получен одним из Волшебников для пары EURUSD за 2016-2017 гг. Получен он был на котировках Дукаскопи, по 100 тиков на 1 бар)
( Читать дальше )
Физико-математические основы Грааля. Часть 5. Дополнение
- 10 января 2021, 15:19
- |
Продолжение.
Начало — здесь: https://smart-lab.ru/blog/668918.php
М-да…
От нечего делать, посмотрел на гистограмму интервалов времени между котировками OPEN 6-секундных баров S6 для пары GBPAUD за ноябрь 2020 г.
Выглядит она вот так:
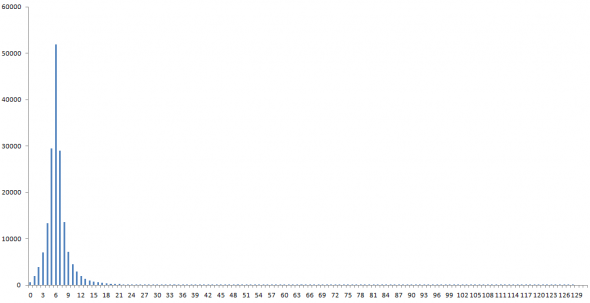
Конечно, это не классическое распределение Эрланга с целым k, а какое-то гамма-распределение… Но, все равно интересно.
А ищем-то мы что?
Какие-нибудь закономерности на фазовой плоскости XY.
Мы должны узреть какие-либо отличия рыночного процесса от случайного и начать безудержно стричь наличные, пока не поздно.
Как говорит мой авторитетный друг — «надо срочно начинать ломать хребет Форексу». И ведь что-то в его словах есть! Да-да… Благая цель.
Так вот, конечно, зависимость текущего приращения от предыдущего на рынке очень красива:
( Читать дальше )
Начало — здесь: https://smart-lab.ru/blog/668918.php
М-да…
От нечего делать, посмотрел на гистограмму интервалов времени между котировками OPEN 6-секундных баров S6 для пары GBPAUD за ноябрь 2020 г.
Выглядит она вот так:

Конечно, это не классическое распределение Эрланга с целым k, а какое-то гамма-распределение… Но, все равно интересно.
А ищем-то мы что?
Какие-нибудь закономерности на фазовой плоскости XY.
Мы должны узреть какие-либо отличия рыночного процесса от случайного и начать безудержно стричь наличные, пока не поздно.
Как говорит мой авторитетный друг — «надо срочно начинать ломать хребет Форексу». И ведь что-то в его словах есть! Да-да… Благая цель.
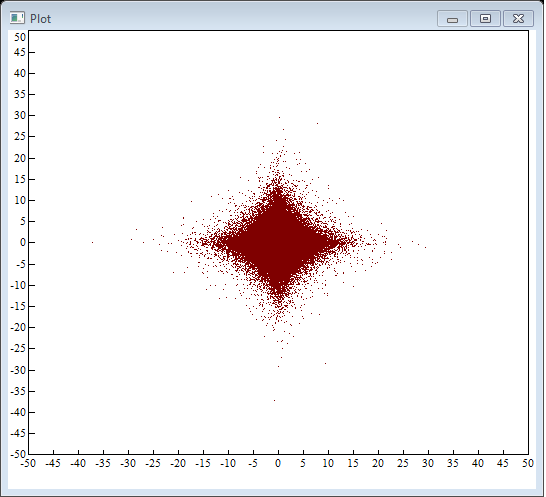
Так вот, конечно, зависимость текущего приращения от предыдущего на рынке очень красива:

( Читать дальше )
Физико-математические основы Грааля. Часть 5
- 08 января 2021, 13:11
- |
Время…
Именно Оно является Граалем на рынке. Ибо тайна Его бесконечна и открывает Врата Тихого Дома для страждущих.
Покажем это.
Рассмотрим графически зависимость текущего приращения от предыдущего в виде набора точек на фазовой плоскости XY, где ось X — текущие приращения Return(t), ось Y — предыдущие приращения Return(t-1).
1. Гауссовские приращения для винеровского процесса без сноса (использовался ГСЧ N(0,1))
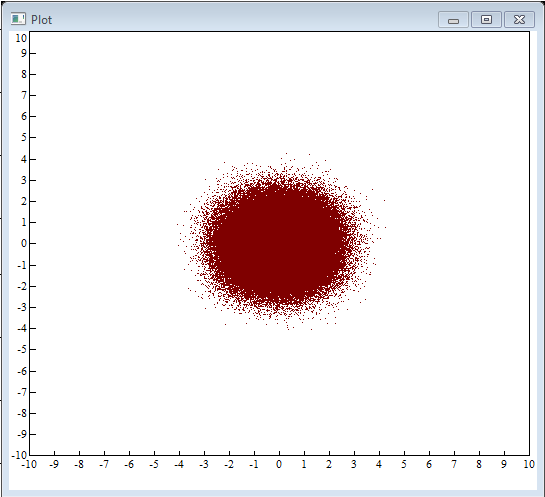
На таком процессе, согласно теории, практически невозможно заработать.
2. Приращения OPEN M1 для EURUSD за 2019 год.
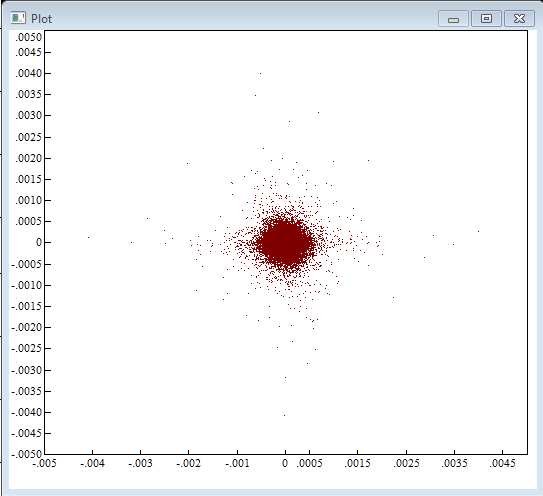
( Читать дальше )
Именно Оно является Граалем на рынке. Ибо тайна Его бесконечна и открывает Врата Тихого Дома для страждущих.
Покажем это.
Рассмотрим графически зависимость текущего приращения от предыдущего в виде набора точек на фазовой плоскости XY, где ось X — текущие приращения Return(t), ось Y — предыдущие приращения Return(t-1).
1. Гауссовские приращения для винеровского процесса без сноса (использовался ГСЧ N(0,1))

На таком процессе, согласно теории, практически невозможно заработать.
2. Приращения OPEN M1 для EURUSD за 2019 год.

( Читать дальше )
Физико-математические основы Грааля. Часть 4
- 03 января 2021, 11:01
- |
Всех с Новым Годом!
И, хотя, судя по отчетам, на СЛ, сплошь и рядом, одни миллионеры — я продолжу Сказание о Граале. Авось, все-таки, найдутся нищие и обездоленные страждущие, которым это будет интересно.
Вообще говоря, идея стратегии «возврат к среднему» (mean reversion) абсолютно не нова, многие потеряли на ней свои депозиты. Но, тяга к ней — бесконечна.
Ибо, мало того, что наиболее подходящая к рыночному, модель марковского процесса Variance Gamma Process имеет тенденцию возврата к матожиданию
![Физико-математические основы Грааля. Часть 4 E[X(t)] = \theta t](https://wikimedia.org/api/rest_v1/media/math/render/svg/87663f79ebb161f3a396db2e3046a79d8b91196e)
(т.н. смещению (дрифту))
так и все немарковские процессы обладают свойством цикличности, что подтверждает Шелепин Л.А. в своих работах:

( Читать дальше )
И, хотя, судя по отчетам, на СЛ, сплошь и рядом, одни миллионеры — я продолжу Сказание о Граале. Авось, все-таки, найдутся нищие и обездоленные страждущие, которым это будет интересно.
Вообще говоря, идея стратегии «возврат к среднему» (mean reversion) абсолютно не нова, многие потеряли на ней свои депозиты. Но, тяга к ней — бесконечна.
Ибо, мало того, что наиболее подходящая к рыночному, модель марковского процесса Variance Gamma Process имеет тенденцию возврата к матожиданию
![Физико-математические основы Грааля. Часть 4 E[X(t)] = \theta t](https://wikimedia.org/api/rest_v1/media/math/render/svg/87663f79ebb161f3a396db2e3046a79d8b91196e)
(т.н. смещению (дрифту))
так и все немарковские процессы обладают свойством цикличности, что подтверждает Шелепин Л.А. в своих работах:

( Читать дальше )
Физико-математические основы Грааля. Часть 3
- 27 декабря 2020, 21:07
- |
Так вот.
Эйнштейн вывел настолько универсальную формулу среднеквадратического отклонения случайного процесса, что трудно не воспользоваться ей в своих интересах.
На вопрос: «а справедлива ли формула Эйнштейна-Смолуховского в ее частном случае, а именно:

естественно, должен быть выдан положительный ответ. Собственно, все данные исследований говорят именно об этом.
Относительно центральной меры тенденции случайного процесса, который протекает на рынке, это дает хорошее приближение к той величине отклонения, от которой начинается „возврат к средней“.
Однако, читателей не должно вводить в заблуждение, что данная формула справедлива для любых интервалов времени и для любых временных периодов.
Собственно, Относительное Время рынка относительно Абсолютного Времени дает именно такие возможности использования данной формулы. Иначе — нет.
Аминь.
С уважением,
Toddler
Эйнштейн вывел настолько универсальную формулу среднеквадратического отклонения случайного процесса, что трудно не воспользоваться ей в своих интересах.
На вопрос: «а справедлива ли формула Эйнштейна-Смолуховского в ее частном случае, а именно:
Коэффициент диффузии броуновской частицы связывает средний квадрат её смещения x (в проекции на произвольную фиксированную ось) и время наблюдения τ:

естественно, должен быть выдан положительный ответ. Собственно, все данные исследований говорят именно об этом.
Относительно центральной меры тенденции случайного процесса, который протекает на рынке, это дает хорошее приближение к той величине отклонения, от которой начинается „возврат к средней“.
Однако, читателей не должно вводить в заблуждение, что данная формула справедлива для любых интервалов времени и для любых временных периодов.
Собственно, Относительное Время рынка относительно Абсолютного Времени дает именно такие возможности использования данной формулы. Иначе — нет.
Аминь.
С уважением,
Toddler
Физико-математические основы Грааля. Часть 2
- 20 декабря 2020, 12:31
- |
При обсуждении основ построения граальной ТС, у страждущих возникли философские вопросы:
1. а где математика, где вожделенные формулы?
2. а зачем нужно распределение Эрланга для интервалов времени между котировками? Мы-де привыкли все делать, используя OHLC, и Грааль и так уже давно у нас в руках.
Постараюсь ответить на эти вопросы.
1. Вся математика с вожделенными формулами описана в теории диффузионных случайных процессов. Могу порекомендовать следующую литературу:
Гардинер К.В. «Стохастические методы в естественных науках»
Попов П.В. «Диффузия»
применительно к финансам:
Rama Cont, Peter Tonkov «Financial Modelling with jump processes»
Фактически, все сводится к анализу уравнений Ланжевена или Фоккера-Планка для движения диффундирующей частицы.
Для практических целей, необходимо изучить вид распределения приращений протекающего процесса и воспользоваться формулами конкретной подходящей модели.
К примеру, вид распределения приращений цены на рынке подобен распределению приращений для Variance Gamma Process:
( Читать дальше )
1. а где математика, где вожделенные формулы?
2. а зачем нужно распределение Эрланга для интервалов времени между котировками? Мы-де привыкли все делать, используя OHLC, и Грааль и так уже давно у нас в руках.
Постараюсь ответить на эти вопросы.
1. Вся математика с вожделенными формулами описана в теории диффузионных случайных процессов. Могу порекомендовать следующую литературу:
Гардинер К.В. «Стохастические методы в естественных науках»
Попов П.В. «Диффузия»
применительно к финансам:
Rama Cont, Peter Tonkov «Financial Modelling with jump processes»
Фактически, все сводится к анализу уравнений Ланжевена или Фоккера-Планка для движения диффундирующей частицы.
Для практических целей, необходимо изучить вид распределения приращений протекающего процесса и воспользоваться формулами конкретной подходящей модели.
К примеру, вид распределения приращений цены на рынке подобен распределению приращений для Variance Gamma Process:
( Читать дальше )
Физико-математические основы Грааля. Часть 1
- 19 декабря 2020, 16:00
- |
Ну, не знаю...
Подарить, что ли, основы построения Грааля страждущим на Новый Год?
Душа болит за рыцарей, бьющихся с бездной… Э-хе-хе....
Ладно. Поехали...
1. Котировки должны приниматься с интервалами времени, удовлетворяющими распределению Эрланга.
Вы должны быть уверены, что поток событий на рынке имеет последействие определенного порядка. Сие есть «память» рынка.
Это - основная парадигма построения граальной ТС. Без достижения этой цели, Вы обречены бороться с рынком как с СБ, математически победить которое очень сложно. Но, можно. Это есть — Относительное Время Системы.
2. Ваша модель должна быть вероятностной.
Это означает, что Вы должны быть готовы как к победам, так и к поражениям. Однако, вероятность победы (получения профита) должна быть выше вероятности поражения. Если для СБ достаточно теоретически доказанных 66% вероятности возвращения к среднему, то эта вероятность должна быть максимально преобразована в деньги.
( Читать дальше )
Подарить, что ли, основы построения Грааля страждущим на Новый Год?
Душа болит за рыцарей, бьющихся с бездной… Э-хе-хе....
Ладно. Поехали...
1. Котировки должны приниматься с интервалами времени, удовлетворяющими распределению Эрланга.
Вы должны быть уверены, что поток событий на рынке имеет последействие определенного порядка. Сие есть «память» рынка.
Это - основная парадигма построения граальной ТС. Без достижения этой цели, Вы обречены бороться с рынком как с СБ, математически победить которое очень сложно. Но, можно. Это есть — Относительное Время Системы.
2. Ваша модель должна быть вероятностной.
Это означает, что Вы должны быть готовы как к победам, так и к поражениям. Однако, вероятность победы (получения профита) должна быть выше вероятности поражения. Если для СБ достаточно теоретически доказанных 66% вероятности возвращения к среднему, то эта вероятность должна быть максимально преобразована в деньги.
( Читать дальше )
Модель рынка как немарковского процесса. Часть 12. Завершение исследований
- 14 декабря 2020, 21:06
- |
М-да...
Читаю, читаю Смартлаб… А чё читаю? Кому? Зачем??? Понятия не имею...
Пожалуй, единственным побуждающим мотивом остается наглядная демонстрация страждущим, что рынок можно победить. Что древние Знания, дарованные Волшебниками, все-таки работают.
Марковские и немарковские процессы, рождение и смерть, счастие и несчастье, прошлое и будущее — все это описывается набором уравнений и ничто не способно изменить сей порядок Бытия.
После НГ начну борьбу с рынком уже на реальном счете.
А полугодовые тестовые торги, дали следующий результат
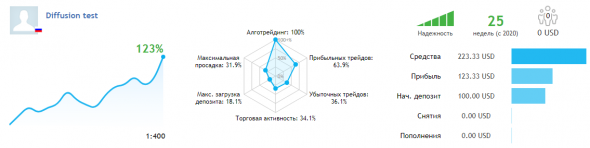
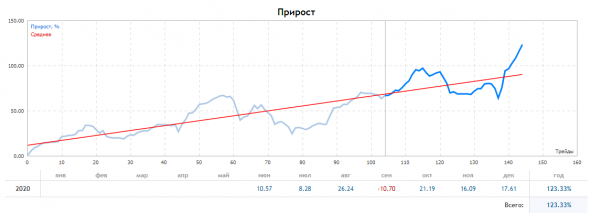
( Читать дальше )
Читаю, читаю Смартлаб… А чё читаю? Кому? Зачем??? Понятия не имею...
Пожалуй, единственным побуждающим мотивом остается наглядная демонстрация страждущим, что рынок можно победить. Что древние Знания, дарованные Волшебниками, все-таки работают.
Марковские и немарковские процессы, рождение и смерть, счастие и несчастье, прошлое и будущее — все это описывается набором уравнений и ничто не способно изменить сей порядок Бытия.
После НГ начну борьбу с рынком уже на реальном счете.
А полугодовые тестовые торги, дали следующий результат


( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал