улыбка волатильности

Сегодня я немного написал про улыбку волатильности (http://smart-lab.ru/blog/136550.php) как функцию волатильности от цены и от страйка.

И естественно протестировал вариант торговли с ее использованием. Результат тестирования и правила использования чуть ниже. 

После сравнения со стратегией описанной мной ранее 

(Описание идеи торговли волатильностью (идея управления портфелем) здесь http://smart-lab.ru/blog/124999.php и Оптимизация стратегии здесь http://smart-lab.ru/blog/126805.php)

задался вопросом: а нужно ли рассчитывать свою улыбку?

Правила входа: Продажа опциона, если его волатильность больше рассчетной волатильности.
Правила выхода: Покупка опциона, если его волатильность меньше рассчетной волатильности.
Управление портфелем: Дельтахеджирование каждый час.

Вот график для сравнения результатов.

 
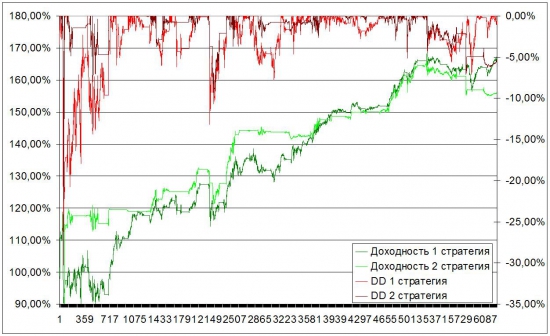
Где преимущесва расчета своей улыбки? 

Продолжая популярную сейчас тему с моделями улыбки волатильности, хочу поделиться результатами своего исследования на эту тему. Немного стремно делать это после поста Виталия Курбаковского. Но может кому-то и мое исследование будет интересно. Сам я не математик и не трейдер, просто программист. Поэтому не судите строго.
 
Наблюдая за поведением улыбки волатильности, уже давно мучали вопросы: Почему улыбка поднимается то вверх, то вниз? Почему она изогнута именно так, а не иначе? Почему перекатывается за текущей ценой БА, причем дно улыбки справа от БА и только к экспирации подтягивается к БА и улыбка становится симметричной? Почему ветви у нее то поднимаются, то опускаются? И главный вопрос: Что является причиной возникновения улыбки волатильности? В некоторых источниках утверждают, что улыбка возникает из-за толстых хвостов распределения приращений. Решил проверить это и провести небольшое исследование.
 
Насколько понял теорию вопроса, чтобы посчитать свою улыбку волатильности, нужно иметь распределение вероятностей, какой будет цена БА на экспирацию (в дальнейшем — распределение цен). Если знать это распределение, то можно однозначно вычислить цены опционов на каждом страйке, и потом, используя формулу Блека-Шоулза, можно вычислить IV на каждом страйке, и получить улыбку волатильности. Как можно получить распределение цен? Решил построить его, генерируя тысячи случайных траекторий цены, начиная с текущего значения БА. Конечные точки траекторий (цена БА на экспирацию) сохраняю, и в конце смотрю, как часто цена попадала в тот или иной диапазон. Так получаю распределение цен на экспирацию. Для построения случайной траектории решил использовать распределение приращений, которое реально было на рынке (в дальнейшем — эмпирическое распределение). Вот, например, распределение приращений (на минутках) для фьючерса RTS-9.11:


( Читать дальше )

Обращаюсь к бывалым опционщикам.
Наверняка вы писали себе какие-то проги или примочки к квику.
Наверняка кто-нибудь сохранял периодически раз в день (час) таблицы опционов в базу данных или файл. Всем бы пригодилась для тестинга стратегий история цен опционов RI с маржируемой её части — с 2009 года.
Может у кого-то есть такое богатство хотя- бы с 2010 года.
Сам научился программой читать таблицы из квика в 2011 году, молодой был, зелёный, не просёк это дело сохранять, да вроде как незачем было, казалось я и так всё знаю, зачем мне что-то тестить. Теперь то оно понятно, что спутал растущий тренд с гениальностью. ))
Если у кого есть такое богатство как история цен опционов или улыбок+IV, поделитесь пожалуйста? Или тыкните носом где можно это дело посмотреть в открытом доступе? По поиску ничего не нашёл.
Сам я начну собирать эту историю со следующего контракта (RIU3), это будет улыбка+IV. Если чо, пользователям смартлаба будут льготные расценки на закачку этой истории, когда она накопится. :-D (шутка)
Заранее спасибо.

Продолжаю тему, поднятую в статье «Толстые хвосты и эмпирические распределения». Напоминаю, в материале рассматривался вопрос, как влияют толстые хвосты распределения цены базового актива на появление улыбки волатильности. В представленной модели фьючерс РТС каждый день прыгает на величину, случайно выбранную из ряда его ежедневных приращений в прошлом. Ранее были показаны результаты модели для 100 шагов движения цены. К ним мы еще вернемся, а пока рассмотрим, что происходит при небольшом количестве шагов модели. В этом случае, Центральная Предельная Теорема только начинает работать, и толстые хвосты разворачиваются во всей своей павлиньей красе.




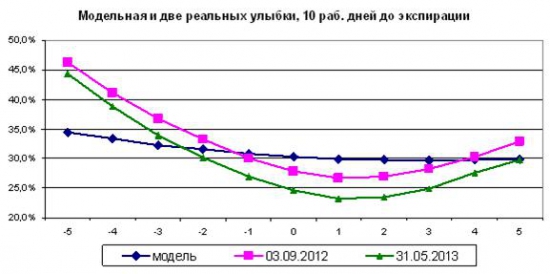
Выше представлена модельная улыбка за 10 дней и две реальных кривых волатильности опционов с аналогичным сроком жизни. Как и раньше, в модели введена поправка на тренд. По оси Х номер страйка от центрального, графики совмещены по горизонтали. 


( Читать дальше )

Финансовые рынки обладают известным свойством – толстые хвосты в распределении приращений актива. Обычно, для демонстрации эффекта сравнивают два графика дневной доходности – для исторического распределения цен и нормального. На рисунке ниже четко заметны выбросы в распределении доходности индекса вдалеке от центра. 
 


Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в  начальной точке,  ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже



( Читать дальше )

Финансовые временные ряды помимо толстых хвостов в распределении доходностей часто демонстрирует так называемый эффект левериджа: когда волатильность возрастает со снижением рынка и, наоборот, снижается, когда рынок растет.
Влияет ли данный эффект на стоимость опционов? Попробуем разобраться.
Для этого, для начала, посчитаем коэффициент корреляции Пирсона для рядов однодневных доходностей и волатильности «на центральном страйке». Будем использовать рыночные данные для фьючерса на индекс РТС и его опционов (3/2010 — 5/2013). Причем будем рассматривать только опционы, до экспирации которых осталось от 45 до 5 календарных дней. Доходности будем получать по формуле: ret[t] = log(S[t]/S[t-1]). Волатильность «на центральном страйке» будем определять как IV0[t] = f(par[t], x=0),  где par[t] — вектор параметров функции f, описывающей рыночную улыбку на конец торгового дня t; x = log(K/S) — «денежность» опциона со страйком K при цене базового актива S.
Т.о. перед нами два ряда ежедневных логарифмических доходностей: ret[t] = log(S[t]/S[t-1]) и rvol[t] = log(IV0[t]/IV0[t-1]).


( Читать дальше )

С практикующими трейдерами на опционном рынке хотелось бы пообщаться на тему сложных математических моделей. Сейчас известно несколько моделей, которые могут найти применение на практике. Например, модель Бруно Дюпире(http://www.globalriskguard.com/resources/deriv/pric_hedg_with_smile.pdf), stochastic vol model, local vol, модель хестона итд. Какие из них видите наиболее эффективными к примеру для использования на фортсе? Использует ли кто-нибудь методы эконометрики(Garch-и) в построении улыбок? Насколько это эффективно? Если у вас имеется модельный трейдинг, то насколько модель устойчива, есть ли проблемы с подгонкой параметров и производите ли переоптимизации модели в сложные периоды(рост волы, падение волы)? Какие программные средства используете для своих вычислений? Если не секрет программными продуктами какой компании пользуетесь или сами разрабатываете софт? 

Немного про свою торговлю. В модельном трейдинге я для себя нашёл пока одну единственную модель stochastic vol, которую согласуя с некоторыми расчётами, использую для построения смайла. Описание модели здесь 

( Читать дальше )

http://www.lektorium.tv/lecture/?id=14010

а вы «Каленкович, Каленкович ...» :-)

Вот интересно, а почему форма кривой с растущими концами, а не падающими, как распределение гаусса?
ведь логично бы предположить что должно быть именно так!?
где ошибка в рассуждениях?

Вопрос: где можно посмотреть улыбку опционов на СнП и Дакс или любых других американско-европейских активов? Есть какие-нибудь сайты?