machine learning
Как работает Machine Learning.
- 01 января 2021, 22:30
- |
Но пользователи часто забывают одно правило: мусор на входе — мусор на выходе. Для обучения недостаточно сделать обучающую последовательность с правильными ответами — результатом будут хорошие результаты на обучающей последовательности, и никакие на реальных данных.
Таким образом, мы должны четко себе представлять, чему именно мы учим, и это вовсе не правильные ответы, а правильные ответы на правильные вопросы. Если не хотите получать дурацкие ответы — не задавайте дурацкие вопросы.
Т.е., для обучения МЛ нам нужно сформулировать адекватные вопросы и ответы на них. Только в этом случае метод МЛ реально обучится и будет реально работать не только на обучающейся последовательности.
Вопрос ещё в том, что обычно мы не знаем и правильных вопросов.
Но это дело поправимое Мы формируем какую либо гипотезу, например — три солдата показывают нам то-то и то-то. Мы как-то ищем этих трёх солдат на истории, там же находим ответы на них, обучаем на этом метод МЛ, проверяем на независимом отрезке истории, и выясняем — действительно ли эти 3 солдаты так важны для нашей торговли, или ну их на фиг.
Понятно, что и при обучении и на реале нам надо задавать МЛ только значимые вопросы, а именно, показывать МЛ не все данные подряд, а только наших трёх солдат.
Ну, а если солдаты воевать не желают, проверяем значимость вороны на шесте.) И так, пока действительно не найдем что-то стоящее.
- комментировать
- ★2
- Комментарии ( 26 )
Создать хедж фонд
- 04 ноября 2020, 23:12
- |
Есть у меня знакомый в Торонто, имеет свой private equity бизнес. Сейчас он задумался о вопросе создания хедж-фонда для диверсификации. Он очень ориентирован на AI, machine learning, генетические алгоритмы и т.д.
Вопрос, собственно, такой — насколько реально найти под такие задачи команду, которая возмется за разработку стратегии, и где вообще начинать искать таких людей?
Чем проще тем лучше.
- 28 сентября 2020, 16:36
- |
Так как показатели roc_auc_score, confusion_matrix, accuracy_score нас как трейдеров мало интересует, нас интересует потенйциальный гешефт, переводим сразу все в финансовые результаты, а именно профитность сделки.
Получилось что то вроде этого:
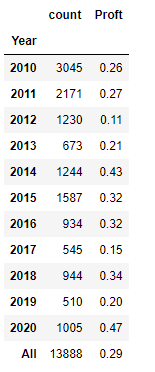
Это все сделки, но их надо почистить, убрать сдвоенности. Допустим у вас за день 10 сделок выскочило, в разное время, но находясь в момент срабатывания первой сделки вы не в зная будут ли сегодня еще сигналы, совершаете сделку сразу на все. Или например на 2 фишки сработал сигнал одновременно. Но реально то сделка будет одна, так к чему нам вместо 1 реальной сделки рисовать две? Поэтому в следующей таблице уже представлены не сделки, а средняя профитность дней и их количество.
( Читать дальше )
ML для поиска закономерностей по Atamanу.
- 27 июля 2020, 13:29
- |
Я сделал три цикла с GradientBoosting, и ограничил глубину деревьев 3. Вуаля!
Здесь можно посмотреть как это выглядит на питоне + база данных+ код WealthLab.
Результаты?
Ну вот например на тренировочной выборке 2010-04.2018 нашлось такое:
if ((AroonDownClose_20_[Bar] >= 75.0)&&(AroonDownClose_20_[Bar] <= 100.0)) //
if ((StochD14_5_[Bar] >= 1.9416)&&(StochD14_5_[Bar] <= 10.3487)) //
Загоняем, считаем:
| Названия строк | Коли | Profit % |
( Читать дальше )
Что я понял, обучая модели.
- 05 июля 2020, 12:53
- |
Вернее так: что я увидел, обучая модели. Всякие подобные темы любят поднимать трейдеры, они отлично располагают для пространных рассуждений о рынке и жизни, а я это, можно сказать, увидел наглядно. В общем, наблюдения не что-то гениальное, мной открытое, не грааль, но я это наблюдаю.
Что я делаю:
Играюсь с моделями ML, играюсь гипер-параметрами – параметрами самих моделей непосредственно и моими какими-то входящими параметрами. Смотрю как меняются результаты в зависимости от этих параметров.
Что я увидел:
- Где-то закономерностей объективно больше, где-то объективно меньше. Если прочесываешь график моделями (с разными параметрами) по мат. ожиданию OOS результатов совокупности моделей и по их распределению видно, что из каких-то графиков закономерности извлекаются на ура, а из каких-то со скрипом. В данном случае график это пересечение по тикер-TF-временной отрезок. Да даже если брать только тикер, некоторые, что называется, палку воткни, она зацветёт, а в некоторых надо очень постараться, чтобы нащупать нормальные закономерности.
- Похоже, действительно легче прогнозировать на короткие интервалы. Но эта закономерность выглядит не так, как её обычно преподносят. Обычно в ходу какая-то такая версия: чем ближе, тем легче, типа на минуты легче, чем на часы и т.д. Я бы сказал, что подтверждение находит скорее следующее: чем больше отношение горизонта прогноза к длине промежутка времени, данные из которого непосредственно участвуют в прогнозе. Ну т.е. если ты принимаешь решение по 50 свечам, то на 2*50 можно прогнозировать с большей точностью (winrate), чем на 10*50 и т.д. При этом в другом контексте, например, если ты ушел на TF выше, ты эти 10*50 сможешь спрогнозировать уже с хорошей точностью.
- Объективно раньше было зарабатывать легче. По ошибке из большого промежутка времени сначала какое-то время брал для обучения данные не самые свежие, а самые древние и удивлялся очень приличным результатам моделей, на свежих данных моделям можно сказать драматически сложнее извлекать закономерности.
Использование метода Монте-Карло для создания портфеля
- 26 апреля 2020, 14:17
- |
Начинающие (да и не только) инвесторы часто задаются вопросом о том, как отобрать для себя идеальное соотношение активов входящих в портфель. Часто (или не очень, но знаю про двух точно) у некоторых брокеров эту функцию выполняет торговый робот. Но заложенные в них алгоритмы не раскрываются.
В этом посте будет рассмотрено то, как оптимизировать портфель при помощи Python и симуляции Монте Карло. Под оптимизацией портфеля понимается такое соотношение весов, которое будет удовлетворять одному из условий:
- Портфель с минимальным уровнем риском при желаемой доходности;
- Портфель с максимальной доходностью при установленном риске;
- Портфель с максимальным значением доходности
Для расчета возьмем девять акций, которые рекомендовал торговый робот одного из брокеров на начало января 2020 года и так же он устанавливал по ним оптимальные веса в портфеле: 'ATVI','BA','CNP','CMA', 'STZ','GPN','MPC','NEM' и 'PKI'. Для анализа будет взяты данные по акциям за последние три года.
#Загружаем библиотеки import pandas as pd import yfinance as yf import numpy as np import matplotlib.pyplot as plt # Получаем данные по акциям ticker = ['ATVI','BA','CNP','CMA', 'STZ','GPN','MPC','NEM', 'PKI'] stock = yf.download(ticker,'2017-01-01', '2019-01-31')
( Читать дальше )
Общий финансовый анализ на Python (Часть 3)
- 05 апреля 2020, 12:51
- |
После всех вычислений, приведенных в этой и этой публикациях, можно углубиться в статистический анализ и рассмотреть метод наименьших квадратов. Для этой цели используется библиотека statsmodels, которая позволяет пользователям исследовать данные, оценивать статистические модели и выполнять статистические тесты. За основу были взяты эта статья и эта статья. Само описание используемой функции на английском доступно по следующей ссылке.
Сначала немного теории:
О линейной регрессии
Линейная регрессия используется в качестве прогнозирующей модели, когда предполагается линейная зависимость между зависимой переменной (переменная, которую мы пытаемся предсказать) и независимой переменной (переменная и/или переменные, используемые для предсказания).
( Читать дальше )
Общий финансовый анализ на Python (Часть 2)
- 22 марта 2020, 13:48
- |
Скользящее окно(Moving Windows)
В заголовке я привел дословный перевод. Если кто меня поправит, и другой термин применяется — то спасибо.
Смысл скользящего окна– с каждым новым значением функция пересчитывается за заданный период времени. Этих функций большое количество. Для примера: rolling.mean(), rolling.std(), которые чаще всего и используют при анализе движения акций. rolling.mean() — это обычная скользящая средняя, которая сглаживает краткосрочные колебания и позволяет визуализировать общую тенденцию.
# Выделяю скорректированную цену закрытия adj_close_px = sber['Adj Close'] # Вычисляю скользящую среднию moving_avg = adj_close_px.rolling(window=40).mean() # Вывожу результат print(moving_avg[-10:])

Дальше построим график, чтоб лучше понять то, что получается в результате работы данной функции:
# Вычисление короткой скользящей средней sber['40'] = adj_close_px.rolling(window=40).mean() # Вычисление длинной скользящей средней sber['252'] = adj_close_px.rolling(window=252).mean() # Построение полученных значений sber[['Adj Close', '40', '252']].plot(figsize=(20,20)) plt.show()
( Читать дальше )
Tорговая система на базе глубокого обучения от начала до реальных торгов. Часть IV. TFX продолжение.
- 14 февраля 2020, 12:46
- |
Однако TFX, как и большинство опен сорс софта, имеет свои проблемы:
- Как я писал в предыдущем посте, компоненты работают в основном только с тренировочным и оценочным (train, eval) наборами данных
- Версия TFX 0.15 работает только с estimator API — однако говорят что в версии 0.21 ввели поддержку keras моделей без конвертирования ее в estimator, к сожалению не удалось это опробовать, так как в этой версии они сломали interactive context. Конечно, можно было бы и без него, просто все компоненты загнать в пайплайн, но хотелось, что бы и в ноутбуке все работало.
- При использовании keras моделей, так и не разобрался как заставить работать TFMA в полную силу, а штука выглядит забавной. Если кто то в курсе, буду рад совету %).
В общем и целом можно смело использовать все эти технологии, но лучше без интерактивных компонентов. Загоняем все в apache beam и строим модельки, проверяем, лучшие используем :). Думаю простейший метод это простой конвейер с функцией трансформации данных и самой моделью. Остальное можно и проигнорировать для домашнего пользования.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал