mt4
Trading Central предлагает новые возможности анализа для MetaTrader с Admiral Markets
- 30 апреля 2019, 10:54
- |

Уважаемые трейдеры,
Мы рады объявить, что новые аналитические плагины Technical Insight и Forex Featured Ideas на базе Trading Central стали доступны для клиентов Admiral Markets на MT4 и MT5!
Новое приложение Admiral Markets, включающее технические идеи Trading Central и Forex, представляет собой мощное расширенное дополнение к платформам MetaTrader 4 и MetaTrader 5. В совокупности эти два новых инструмента расширяют возможности современного трейдера с помощью широкого спектра технической аналитики, торговых индикаторов и лучшего в отрасли распознавания паттернов.
И, кстати, новые плагины уже были отмечены наградами и получили всеобщее признание в мире трейдинга.
Преимущество 1: Определите направление движения актива с Featured Ideas
На Admiral Markets в данный момент вы можете найти более 8000 финансовых инструментов, и отслеживать абсолютно все движения рынка вручную невозможно. Здесь вам может помочь аналитический плагин Featured Ideas™.
( Читать дальше )
- комментировать
- ★1
- Комментарии ( 3 )
Сбросил бесплатно все свои старые версии торговых советников для MT4. Форекс, крипта
- 07 февраля 2019, 11:22
- |
clc.to/TradingClubs
Если кому интересны астро-исследования рынков. SP500, RTS, ...
- 09 января 2019, 16:45
- |
Смотрим. Тыкаем мышью рисунок, чтобы разглядеть.
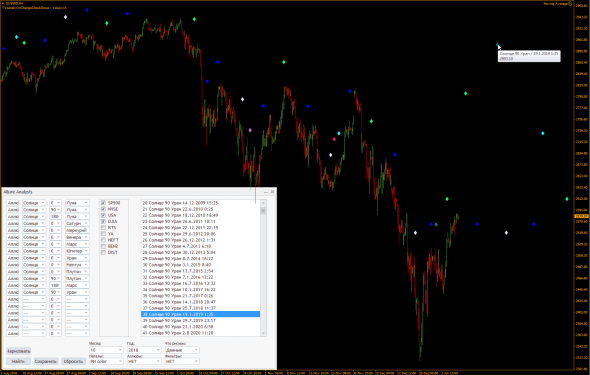
Поначалу кажется, что нечто подобное я показывал в прошлых годах. Вы не ошибаетесь, так и есть. Но также появились дополнения и отличия. Разберем структурно, что здесь такое.
1-ый уровень.
перед нами график SP500 в терминале mt4 (форекс).
Существуют расчеты движения планет, которые есть в любой профессиональной астро-программе. В том числе бесплатных. Именно такие расчеты можно в моей "astro-mt4" набрать ручками, и получить точные кординаты планет на любой график, будь это хоть SP500, хоть евро/доллар, хоть РТС и другие чарты.
Один достойный программист давно реализовал эту возможность, полезную для исследований, но… поскольку веду речь об АСТРО-кластерном анализе, который требует добавить к графику инсайдерскую информацию, который нигде нет, и никогда не будет в астро программках, то… новый программер пошел дальше.
( Читать дальше )
Я прощаю Метаквотам. Всех - С Новым Годом!
- 26 декабря 2018, 15:24
- |
Желаю всем успеха.
Trade well.
Строковый тип данных string в языках MQL4 и MQL5
- 07 ноября 2018, 11:29
- |
Всех приветствую. Продолжаем изучение языка MQL4. В прошлый раз мы говорили о вещественных типах данных, а сегодня поговорим о строковом типе. Начать следует с того, что из себя представляет строка. Строка – это последовательность из юникод-символов. Таблица юникод-символов включает в себя очень много символов, хотя в практическом использовании строк, скорее всего, мы будем пользоваться только теми символами, которые видим на клавиатуре. Сюда входят и буквы, и цифры и знаки пунктуации. Как раз строковый тип данных string и позволяет хранить последовательности из таких символов.
Строки могут быть полезны для вывода какой-либо информации на экран или в журнал. В этом смысле они весьма универсальны, поскольку позволяют совмещать текстовую и числовую информацию. Используя строки, можно обеспечить информативность работы советника, т. е. советник может сопровождать свои действия выводом пояснительных сообщений. Это даёт понять, какой этап алгоритма выполняется в данный момент времени. Так же эти сопроводительные сообщения позволят, в случае возникновения ошибок в работе советника, быстрее сориентироваться где они могли произойти и исправить их.
( Читать дальше )
Нужен брокер с MT4 где есть российские индексы и акции.
- 23 октября 2018, 15:13
- |
Целые типы данных в MQL4 и MQL5
- 19 октября 2018, 12:47
- |
Всех приветствую. Продолжаем цикл уроков по MQL4.
В прошлый раз мы начали тему типов данных, сегодня будем говорить о ней более конкретно. Речь пойдёт о целых типах данных, предназначенных для хранения целочисленных значений. В языке MQL4 их 11 штук и отличаются они друг от друга по количеству места, которое занимают в памяти, и по области значений, которые переменные данных типов могут принимать. Естественно, исходя из этих отличий, иногда рациональнее использовать один тип данных, а иногда другой.
Список целых типов данных в MQL4 выглядит следующим образом:
- char
- uchar
- bool
- short
- ushort
- int
- uint
- color
- long
- ulong
- datetime
Кстати, в языке MQL5 типы данных такие же, так что содержание поста можно смело отнести и к целым типам данных в MQL5.
Все подробности о каждом типе данных с примерами применения можно узнать из закреплённого видео. Спасибо за внимание.
Мысли про евро
- 21 сентября 2018, 10:58
- |
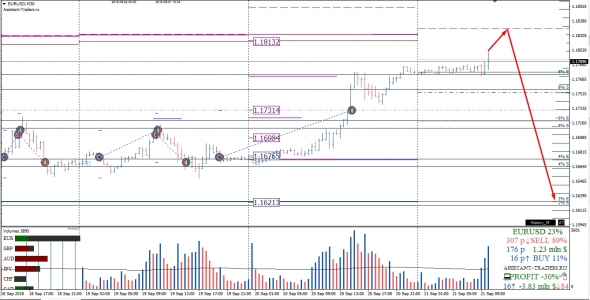
Мысли по евро: ситуация как ни кстати типичная,- перед окончанием недели цена движется в сторону убытка продавца опционов, пробив перед этим несколько опционных уровней сопротивления покупателей опционов. Некоторые трейдеры в шоке, как так опц уровни пробиваются?! А на самом то деле, до экспирации еще есть время опустить цену, ну и самое главное, маркетмейкеру недельных опционов, которые сегодня экспирируются, выгодно любое закрытие ниже 1.1813, поэтому:
а) предполагаем рост до 1.1813
далее
б) закрытие недели ниже 1.1813 или около этой ценовой отметки
или
в) максимально возможное снижение до уровня MAX Paint 1.1622 (самой выгодной цены экспирации текущего недельного опциона для маркетмейкера).
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал