Блог им. ataden
Эмпирический пут-колл паритет или как ломается модель Блэка-Шоузла
- 10 мая 2017, 10:17
- |
Например, купив пут и продав колл на одном страйке, можно создать короткую позицию по БА. Если не соблюдается пут-колл паритет, то можно теперь захеджироваться, купив базовый актив и получить доходность без риска. В риск-нейтральном мире, в котором работает модель Блэка-Шоулза, вы всегда должны такой комбинацией зарабатывать безрисковую процентную ставку. Поэтому точная формула пут-колл паритета выглядит так:
P и С — цены пута и кола, соответственно
Х и S — страйк и цена БА
e-rt — дисконтирующий множитель, приводящий страйк к текущему периоду
Поскольку в системе OptionSmile все показатели нормированы на текущую стоимость БА, т.е. S, будем использовать немного иной вариант паритета:
P-C = X-F
На графике это схематично выглядит так
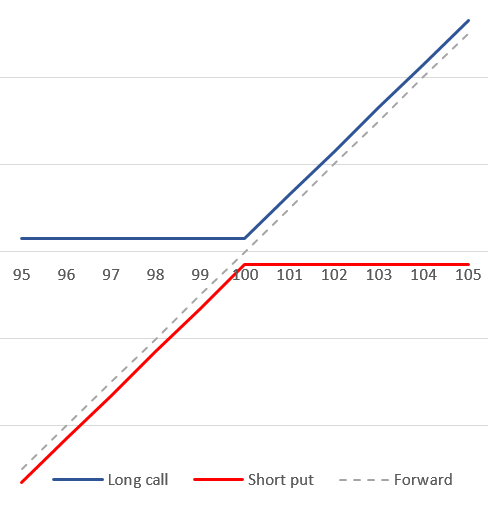
Возьмем режим рынка, который был рассмотрен в одной из методических статей, посвященной анализу распределения доходности БА. Это режим перепроданности (RSI(14)<40) в периоды бычьего рынка или боковика (т.е. отбросим рецессии и медвежьи рынки), рассмотрим 2-недельные опционы на SPY. Вот такая фильтрация получилась:

Видно, как сильно в такие периоды работает mean reversion: рынок в среднем отстреливает вверх на 1.52% за 2 недели (это 38.2% годовых). Посмотрим на оценку опционов — путов и колов. Как и ранее, синий график — справедливая стоимость, красный — гипотетические рыночные цены.
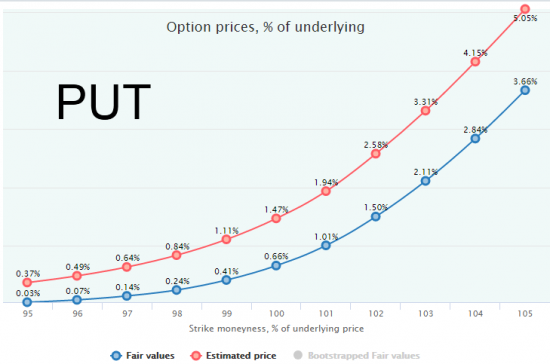
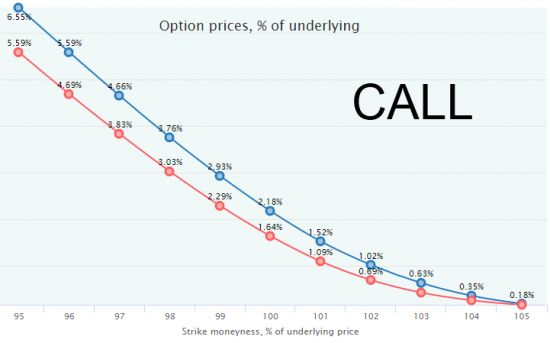
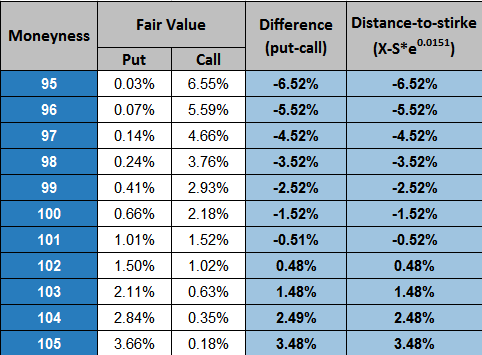
Картина вполне предсказуемая: путы недооценены, колы переоценены из-за сильного ожидаемого движения БА вверх. Посмотрим, что же с пут-колл паритетом. Посчитаем его для безрисковой ставки r = 1% годовых (2 недели до экспирации).
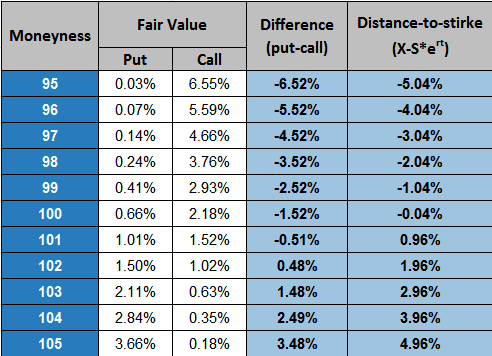
Как видим, паритета даже близко нет! Разница между путами и колами (четвертая колонка) сильно не похожа на разницу между страйком и форвардной ценой (пятая колонка). Т.е. вся модель неправильная?
Нет, на самом деле все верно. Просто до этого мы, как и большинство опционных трейдеров, рассуждали с позиции риск-нейтрального подхода, когда математическое ожидание доходности цены было равно безрисковой процентной ставке. Форвардную цену мы считали, умножая текущую цену S на множитель e-rt, где r — безрисковая ставка (в нашем примере 1% годовых). Конечно, это идеализация, и инвесторы в акции должны получать больше доходность для компенсации повышенного риска (equity risk). Эмпирические данные это подтверждают.
Если мы внимательно посмотрим на разницу между путами и колами в таблице выше, но увидим подозрительную постоянность ее дробной части (0.52% для отрицательной разницы и 0.48 для положительной). Если мы из этой разницы уберем дистанцию между страйком и ценой БА (текущей, не форвардной), то получим 1.52% на всех страйках, что совпадает с ожидаемой доходностью БА в этом режиме — см.самую первую таблицу.
Теперь, думаю, все очевидно. Давайте возьмем форвардную цену как ожидаемую цену БА исходя из нашего эмпирического распределения, а не на базе безрисковой ставки. Вместо rt = 1%*(10/252) = 0.04% (безрисковая ставка на 2 недели) возьмем фактическую доходность 1.52%, а точнее ее логарифм, чтобы привести к непрерывной форме, ln(1.52%) = 1.51%. Вот такой теперь получится паритет:
Как видим, паритет почти идеально выдержан, с точностью до сотых долей процента (из-за округлений). Отсюда логичен вывод: чтобы соблюдался пут-колл паритет, нужно считать форвардную цену БА с помощью процентной ставки, равной мат.ожиданию доходности БА распределения, по которому эти пут и колл были посчитаны. В риск-нейтральном (risk-neutral) мире, в т.ч. в формуле Блэка-Шоулза, эта ставка всегда безрисковая. В реальном мире (real-world) эта ставка выше и отражает так называемое неприятие риска (risk aversion), когда инвестор требует «доплату» за принимаемый риск. В системе OptionSmile в качестве этой ставки принимается фактическая средняя доходность БА за выбранный рыночный режим. В обобщенном виде пут-колл паритет выглядит так:
P-C = X-S*eh
h — математическое ожидание доходности БА в форме непрерывной ставки. Если доходность обозначить дискретной ставкой, то формула будет немного привычнее:P-C = X-S*(1+d)
d — дискретное мат.ожидание доходности базового активаКстати, из-за этого часто бывают парадоксальные результаты, если применить формулу БШ из риск-нейтрального мира к миру реальному. После получения справедливых цен в системе OptionSmile считается и вмененная волатильность по формуле БШ (разумеется, в встроенной безрисковой ставкой). Вот, что выходит для путов из примера выше:
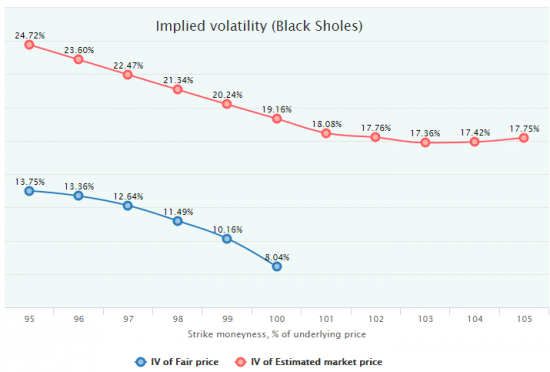
Для страйков в деньгах (денежность > 100) посчитать вмененную волатильность невозможно, т.к. если посмотреть на графики справедливых цен путов выше или в таблицу, то виден парадокс: Fair Value путов меньше их внутренней (intrinsic) стоимости, что для риск-нейтрального мира полная ересь. Получается отрицательная временная стоимость и формула БШ ломается на этом месте.
Однако в реальном мире такое возможно, т.к. в этом конкретном режиме рынка мат.ожидание доходности БА сильно положительное, что очень существенно снижает стоимость хеджирования этого опциона (а это и есть его цена). Конечно, если бы такая была цена на рынке, то нашлось бы много желающих купить такой пут, продать колл и всю конструкцию захеджировать покупкой БА. Доходность без риска была бы равна мат.ожиданию доходности БА, в нашем примере 1.52% (38.2% годовых). Но, разумеется, это не возможно, т.к. при текущей безрисковой ставке близкой к нулю такая доходность была бы сразу ликвидирована (arbitrage out) HFT роботами. А вот если бы сама безрисковая ставка выросла до 38.2%, то опционы на рынке стоили бы стоили приблизительно таких денег, как на синих графиках выше: путы бы сильно подешевели, а колы подорожали. Пока существует диспаритет между этими двумя ставками, будет сохраняться и разница в оценке.
Возникает еще один резонный вопрос, а зачем тут вообще опционы. Можно же просто покупать БА, когда RSI<40 и получать эту вполне себе хорошую доходность (38.2% годовых). Это, конечно, возможно, но придется долго ждать, пока наберется большое количество сделок, чтобы вероятности проявили себя и средняя доходность приблизилась к ожидаемой. Гораздо надежнее эксплуатировать опционную неэффективность и входить в позицию, учитывая статистическую существенность разницы между справедливой и рыночной ценами. См. методическую статью Доверительные интервалы справедливой стоимости.
Интересно, что развитые фьючерсные рынки по разному соблюдают риск-нейтральный паритет на широких индексах акций. Например, у фьючерсов на американские индексы базис (или roll yeld между фьючерсами с разной экспирацией) равен стоимости удержания позиции (cost of carry), которая соответствует безрисковой процентной ставке минус дивидендная доходность. Если дивиденды выше процентной ставке, фьючерсы в бэквордации (отрицательный carry), если наоборот, то в контанго (положительный carry). Но процентная ставка там почти всегда близка к безрисковой, что дает возможность без больших потерь реплицировать long портфель фьючерсами.
У биржи ICE есть интересный сервис для оценки roll yeld для разных фьючерсов - Pace of Roll, где считается вмененная процентная ставка (implied financing rate) и определяется ее спред к Libor. По разным фьючерсам в зависимости от степени contango и backwardation будет разная вмененная ставка, т.е. различная оценка рынком мат.ожидания доходности актива. В частности, по индексу FTSE 100 последний roll (Mar17-June17) проходил с гигантским спредом к Libor 7.75% из-за того, что FTSE100 считается в GBP. А вот по американскому индексу компаний малой и средней капитализации Russell 2000 спред был близок к нулю, т.е. его ожидаемая доходность была близка ставке Libor (1.2%)



















Почитайте внимательнее, пост совсем о другом.
А 1.52% вообще не похоже на дивиденды, т.к. это доходность за 2 недели. Получается 38.2% годовых
А паритет-то как раз получается. В этом вся соль. Просто мера должна быть не риск-нейтральная
Хотя, конечно, рыночные котировки надо очищать, если до экспирации попадают ex-dividend dates.
Пришлю приглашение сейчас.
«Конечно, если бы такая была цена на рынке, то нашлось бы много желающих купить такой пут, продать колл и всю конструкцию захеджировать покупкой БА. Доходность без риска была бы равна мат.ожиданию доходности БА, в нашем примере 1.52% (38.2% годовых). Но, разумеется, это не возможно, т.к. при текущей безрисковой ставке близкой к нулю такая доходность была бы сразу ликвидирована (arbitrage out) HFT роботами. А вот если бы сама безрисковая ставка выросла до 38.2%, то опционы на рынке стоили бы стоили приблизительно таких денег, как на синих графиках выше: путы бы сильно подешевели, а колы подорожали.»
Т.е. тут речь идет не о фактических котировках на рынке, а оценке опционов на базе эмпирической (не риск-нейтральной) меры
Если есть больше, то более подробно на www.optionsmile.ru
В реале, конечно таких котировок нет (синий график). Это оценочная справедливая стоимость
Арбитраж считается всегда на экспирацию, и почему бы не держать позицию до экспирации при нулевой марже?это может быть, но только если они равны — тогда не арбитраж, а если нет — то арбитраж.
А опционы хороши тем, что рынок ошибается не только дирекционно, но и во втором измерении — с оценкой будущей волатильности. Когда RSI<40 рынок перепуган и затаривается путами по безумным ценам. Behavioral Finance!
Да и вроде по теме перекос в опционах — немного направленно в базисе.
Когда в тексте начинают проскакивать слова "риск-нейтральная мера, мартингал или риск-нейтральная вероятность", у меня возникает стойкое ощущение участия в игре с наперстками...
Мы и так можем варьировать ситуацию игрой с ненаблюдаемым параметром IV и зачастую на практике не можем отличить влияние веги от влияния теты.
А если ещё добавить ненаблюдаемый параметр "ставка доходности", то запутать себя становится ещё на порядок легче.