SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. melamaster
Гипотезы о рыночном базисе
- 30 апреля 2018, 12:26
- |
Дисклэймер: далее идет скучный лонгрид.
В 2004-2008 годах мы искали естественное для рынка разложение. Был перебран широкий арсенал от SVD и SSA до спектральных методов типа Фурье-Хаар-вейвлет. Мой кусочек работы был связан с Фурье, Уолшем и вейвлетами. В качестве оценки естественности мы исходили из наивного допущения: что лучше работает, то и естественнее. Лучше — значит обладает лучшими прогнозными свойствами. Т.е., по-простому, какой из базисов позволяет подальше заглянуть (по-честному) в будущее, тот и лучший, стало быть, самый естественный.
Плюс к этому наивному представлению были еще и такие: естественный базис должен не сильно противоречить условиям конечности, нестационарности и т.п. Как это всё проверять? Не очень понятно, но было очевидно, что это необходимо, а также то, что развитая математика не любит нестационарности, конечности, сингулярности и всякое такое прочее.
На 90% рыночным материалом для исследований были данные основных валютных пар (FOREX).
Прежде чем перейти к картинкам, обозначу итоги. Что получилось? Углубиться в проблему, т.е. понять собственное непонимание. Что не получилось? Обрести грааль в виде машинки по печатанию денег. Если оценить без крайностей, то, кажется, что нащупать более предпочтительный базис скорее удалось, чем не удалось. Предпочтительность по косвенным тестам, не по торговому профиту.
Теперь подробнее. Чтобы это было понятно и мне самому, лонгрид будет в стиле комикса. Речь пойдет о демонстрациях преимущества базиса в функциях Уолша над гармониками. Преимущества обнаружены эмпирическим путем исходя из основных методов научного поиска: пальцем в небо и методом тыка. Приводимые примеры не могут претендовать на полноту всех возможных случаев. Однако, случаев преимущества Фурье над Уолшем замечено не было (аналитические преимущества не в счет).
Поскольку с тем, что такое синусоиды, знаком каждый школьник СССР или РФ, а с разложением в ряд Фурье каждый выпускник технвуза и классического университета, про синусоиды напоминать не буду, а про Уолша и Хаара вот такую памятку приведу (ну и про базис тут заодно самые общие формулки):

Ругательное слово секвента это из секвентного анализа ( Хармут Х. Теория секвентного анализа: основы и применения, М., Мир, 1980), где функции Уолша и Хаара рассматриваются с единых позиций. Там есть очень интересные вещи типа диадной корреляции. Парадокс в том, что для финансов при помощи секвентного анализа у меня не получилось (пока) извлечь профит, но немного набравшись в этих функциях опыта, мы их применили в криптографии, расшифровав один шифр, взламывая файл с данными. Такая вот забава.
Визуально фильтрация может выглядеть так:
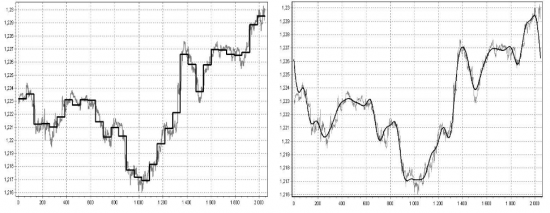
Это если примерно одинаковую часть наиболее значимых компонент (по амплитуде) в спектрах взять. Если взять несколько первых компонент, то фильтрация может выглядеть следующим образом:
По форме распределние амплитуд Уолш-спектра такое вполне себе нормальное:
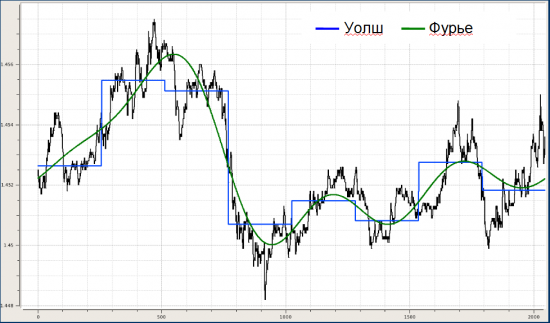
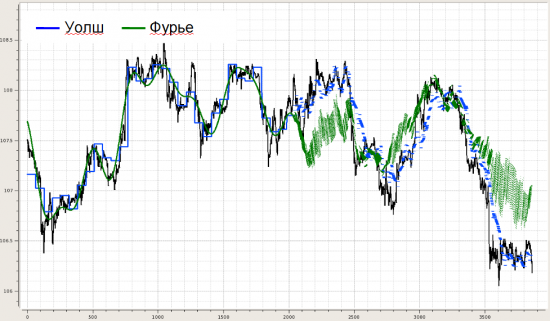
Далее делалась попытка динамического моделирования, чтобы понять, как оно всё адресовано в будущее, если вообще адресовано. Для этого строился динамический след. Берем кусок, делаем два разложения (Уолш и Фурье), запоминаем конец (несколько последних точек), сдвигаем окно разложения на один отсчет, снова фиксируем конец и т.д. Получается картинка такого вида (на примере нулевой+первой функций):
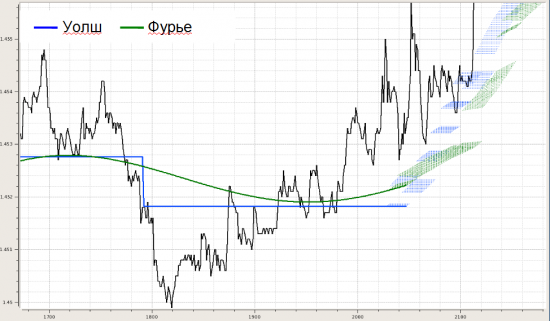
Далее несколько картинок, показывающих, как это может выглядеть для разного кол-ва выбранных функций в фильтрации.
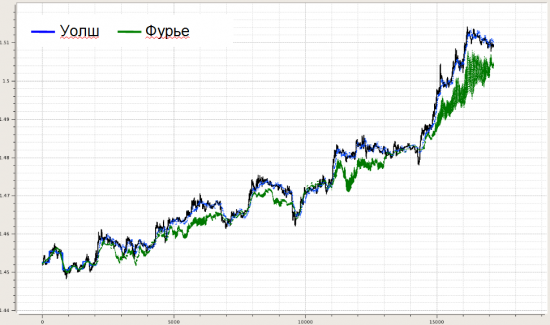
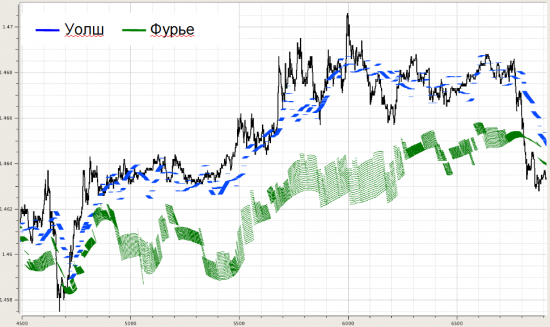
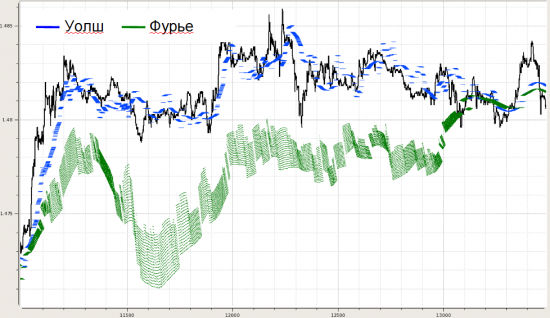
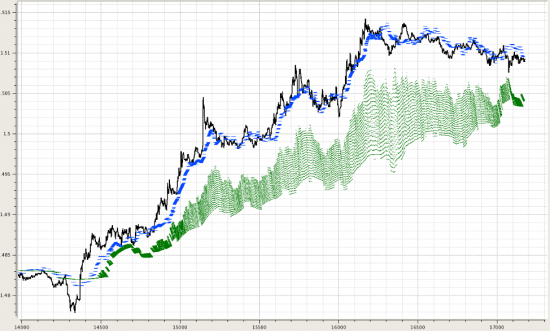
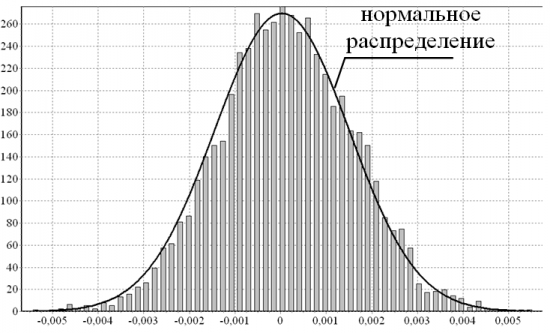
Ну и в плане метрик этого видимого различия строились распределения невязок по концам между реальной котировкой на каждом отсчете и фильтрацией по Уолш- и Фурье-модели:
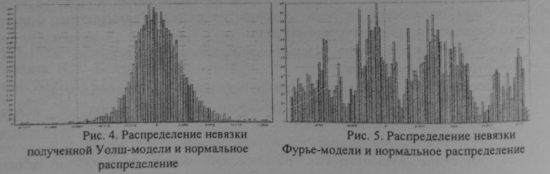
Для Уолша в каждом случае получалось куполообразное распределение с дисперсией, меньшей, чем для дисперсии аналогичной невязки по Фурье.
В 2004-2008 годах мы искали естественное для рынка разложение. Был перебран широкий арсенал от SVD и SSA до спектральных методов типа Фурье-Хаар-вейвлет. Мой кусочек работы был связан с Фурье, Уолшем и вейвлетами. В качестве оценки естественности мы исходили из наивного допущения: что лучше работает, то и естественнее. Лучше — значит обладает лучшими прогнозными свойствами. Т.е., по-простому, какой из базисов позволяет подальше заглянуть (по-честному) в будущее, тот и лучший, стало быть, самый естественный.
Плюс к этому наивному представлению были еще и такие: естественный базис должен не сильно противоречить условиям конечности, нестационарности и т.п. Как это всё проверять? Не очень понятно, но было очевидно, что это необходимо, а также то, что развитая математика не любит нестационарности, конечности, сингулярности и всякое такое прочее.
На 90% рыночным материалом для исследований были данные основных валютных пар (FOREX).
Прежде чем перейти к картинкам, обозначу итоги. Что получилось? Углубиться в проблему, т.е. понять собственное непонимание. Что не получилось? Обрести грааль в виде машинки по печатанию денег. Если оценить без крайностей, то, кажется, что нащупать более предпочтительный базис скорее удалось, чем не удалось. Предпочтительность по косвенным тестам, не по торговому профиту.
Теперь подробнее. Чтобы это было понятно и мне самому, лонгрид будет в стиле комикса. Речь пойдет о демонстрациях преимущества базиса в функциях Уолша над гармониками. Преимущества обнаружены эмпирическим путем исходя из основных методов научного поиска: пальцем в небо и методом тыка. Приводимые примеры не могут претендовать на полноту всех возможных случаев. Однако, случаев преимущества Фурье над Уолшем замечено не было (аналитические преимущества не в счет).
Поскольку с тем, что такое синусоиды, знаком каждый школьник СССР или РФ, а с разложением в ряд Фурье каждый выпускник технвуза и классического университета, про синусоиды напоминать не буду, а про Уолша и Хаара вот такую памятку приведу (ну и про базис тут заодно самые общие формулки):

Ругательное слово секвента это из секвентного анализа ( Хармут Х. Теория секвентного анализа: основы и применения, М., Мир, 1980), где функции Уолша и Хаара рассматриваются с единых позиций. Там есть очень интересные вещи типа диадной корреляции. Парадокс в том, что для финансов при помощи секвентного анализа у меня не получилось (пока) извлечь профит, но немного набравшись в этих функциях опыта, мы их применили в криптографии, расшифровав один шифр, взламывая файл с данными. Такая вот забава.
Визуально фильтрация может выглядеть так:

Это если примерно одинаковую часть наиболее значимых компонент (по амплитуде) в спектрах взять. Если взять несколько первых компонент, то фильтрация может выглядеть следующим образом:

По форме распределние амплитуд Уолш-спектра такое вполне себе нормальное:

Далее делалась попытка динамического моделирования, чтобы понять, как оно всё адресовано в будущее, если вообще адресовано. Для этого строился динамический след. Берем кусок, делаем два разложения (Уолш и Фурье), запоминаем конец (несколько последних точек), сдвигаем окно разложения на один отсчет, снова фиксируем конец и т.д. Получается картинка такого вида (на примере нулевой+первой функций):

Далее несколько картинок, показывающих, как это может выглядеть для разного кол-ва выбранных функций в фильтрации.





Ну и в плане метрик этого видимого различия строились распределения невязок по концам между реальной котировкой на каждом отсчете и фильтрацией по Уолш- и Фурье-модели:

Для Уолша в каждом случае получалось куполообразное распределение с дисперсией, меньшей, чем для дисперсии аналогичной невязки по Фурье.
теги блога Sergey Pavlov
- 2017
- 2020
- 2021
- exante
- just2trade
- lua
- moex
- Quik Lua
- RI
- S&P500 фьючерс
- secret
- TSLab
- VWAP
- акции
- алгоритмический портфель
- алготрейдинг
- апрель
- биржа
- биткойн
- бот
- брокера
- брокеры
- Вестников
- Витковский
- волатильность
- вопрос
- грааль
- деньги
- дивиденды
- дизайн
- заразум
- игры
- иГРЫрАЗУМа2018
- инвестиции
- итоги
- итоги месяца
- июль
- июнь
- канал
- квик
- комон
- контртренд
- конференция
- кукл
- ликвидность
- лотерея
- луа
- ЛЧИ
- люди
- МАЙ
- март
- минутки
- мобильный пост
- натуральный газ
- нефть
- октябрь
- опрос
- опционы
- открытый интерес
- офз
- оффтоп
- пила
- плечи
- поведение
- подгонка
- портфель
- прогноз
- продажа
- проскальзывание
- проскальзывания
- разум
- рецензия на книгу
- РИ
- риск
- ртс
- сбер
- Сбербанк
- сентябрь
- случайность
- счастье
- телеграм
- торговые роботы
- трейдинг
- тренд
- трендовые системы
- тренды
- Тслаб
- тупаны
- убытки
- февраль
- физические лица
- финам
- форум
- фьючерс ртс
- фьючерсы
- чемодан
- шорт
- эквити
- юридические лица
- январь



















** нет, сюда я не вернусь ))
2) Наверное, можно объяснить, почему функции Уолша, действительно, лучше подходят, т.к. лучше отражают неравномерности в движении рынка при использовании времени в качестве горизонтальной шкалы по сравнению с синусоидами.
3) Если не секрет, в чём смысл публикации такого поста именно на Смарт-Лабе? Раздача того, чего не жаль (у меня не получилось, больше в этом направлении не работаю, но у кого-то другого, может, и получится)? Поиск единомышленников или хотя бы адекватных персонажей? Ещё что-то?
Я в свое время тоже этой темой баловался, хотя ограничился лишь классическим exp(iwt) фурье. И пришел к выводу, что ценности там ноль, как в плане предсказания, так и в плане объяснения прошлого. И сейчас, когда я иногда пытаюсь понять, как бы фурье мог бы помочь найти мне хоть какую-то из имеющихся в арсенале систем--я неизменно прихожу к выводу, что никак. Есть ли какой-то смысл в таких разложениях, хоть по синусоидам, хоть по любым другим базисам?
anatolyutkin, Николай Скриган рассказывает не первый год, что "Фурье чудесно работает. Только Вы лично его готовить не умеете. Но я-то умею. ;-) ".
anatolyutkin, в соседней ветке на днях искали конструктив: https://smart-lab.ru/blog/468221.php
Не нашли (
По крайней мере один из последних постов про "уход счета ниже уровня оговоренного риска" как бы намекает…
Во-первых, помним, что любая аналитическая функция может быть представлена композицией гармоник, экспонент, полиномов или авторегрессией. В некотором роде это всё одно и то же. Что-то удобнее анализировать, что-то удобнее вычислять и тд. Поэтому, если мы и пытаемся применять матаппарат к рынку, то чуда ждать не надо. Если работает что-то, то работает и другое. Хорошо бы найти технику и границы.
Во-вторых, я исхожу пока из простой модели. Рынок (на моём тайм-фрейме торговли) = сигнал+шум. Сигнал, видимо, сложный с переменой структурой во времени. Шум тоже не просто какой-то гаусс. Тут ваша ремарка подходит про надежду на выделить основную функцию, которая хотя бы помогала статистически разделять на сигнал и шум. Но это надежда, не более.
Может, покопаем в другую сторону?
У нас есть два варианта:
1. Рынок случаен (Херст == 0.5) — ловить нечего.
2. У рынка есть Херст != 0.5. Тогда можно строить прогноз, используя предыдущую историю.
Есть мнение, что уже все изобретено. Только формулки немного мутные на первый взгляд...
Итак… есть ли версии, что такое не только волатильность рынка, но и еще и персистентность? Вот смотрите… набившее оскомину 9апреля… рынок монотонно движется в одну сторону… ну если по уму… то волатильность стремится к нулю… а мы все говорим, что волатильность подскочила… и HV в космос, а IV подавно...
Sergey Pavlov, оценивать Херста — то еще упражнение. Нужно окно нереального размера, чтобы получить оценку с приемлемой точностью. Или Вы умеете это делать эффективней?
Конкретно 9 апреля понятно что случилось. Был процесс, условно, с Херстом 0.50-0.55. На выходных нам втыкают санкции — и начинается процесс условно с Херстом 0.6-0.7. Всего дня 2-3 продлился этот режим.
=) А сколько эмоций в итоге.
Sergey Pavlov, в одной из лекций Кирилл Ильинский рассказывал как меряют Херста с помощью вейвлетов (если ничего не путаю).
Но при этом было сделано очень важное (на мой взгляд) замечание: "Это искусство. Все понимают, что примерно надо делать. Но когда речь идет об ограниченных дискретных выборках, 10 исследователей получат 10 разных результатов.".
_
Вы понимаете, что «рынок случаен» и «Херст == 0.5» — не тождественные утверждения? Херст может быть равен 0.5 у неслучайного ряда.
_
Элементарный пример: берём два ряда — один с Херст=0.4, второй с Херст=0.6 — и чередуем их в виде «зебры». Какой будет Херст у этой зебры?
Ivan FXS, при чередовании рядов Вы разрушаете внутреннюю структуру данных. Если будете переключать достаточно часто — в итоге получите ряд с херстом 0.5, который будет непригоден для зарабатывания.
И да: я понимаю разницу между разными видами случайности. В данном случае более точно сказать так: "Рынок является геометрическим броуновским движением БЕЗ ПАМЯТИ? Следовательно, Херст == 0.5 и ловить нечего".
Учитывая, что нормально измерить Херста крайне затруднительно, то из утверждения «мы немеряли херста равного 0.5 нельзя сделать никаких выводов относительно того можно или нет заработать.
Но это некий звоночек, что „будет крайне трудно“. Не рациональней ли искать процессы с явным отклонением Херста от 0.5 и работать с ними?
Ivan FXS, Вы по физике экспериментальные лабораторные работы делали? В школе или в ВУЗе? Помните методику измерений?
Вот и ответ. Делаю строго по науке «теория измерений».
Ivan FXS, =) встречал. И с 0.7 и с 0.8, и с 0.3-0.4. Когда сам генерировал серии.
Если коротко, то точность известных мне методик фактически не позволяет отличить Херст 0.55 от Херста 0.50. Это делает попытку плясать от показателя Херста бессмысленной.
А на реальном рынке Херсты по всей видимости лежат в интервале максимум 0.45-0.60. И как Вы верно подметили — еще и меняют режим временами.
Поэтому пока мы не разработаем крайне эффективную методику измерения показателя Херста — счастья не будет.
ПС Когда-то пытался научиться еще считать показатель Гёльдера, но не довел до конца. Если у кого-то есть готовый код или ссылка на внятную статью с описанием процедуры — буду благодарен.
_
Другое дело, что для других пар лагов [на том же самом исследуемом ряде P(i) ] — например, L=1 и L=3 (или L=11 и L=33) — статистика «показатель Херста» будет иметь некоторое другое (или ещё одно другое) значение.
Ivan FXS, =) не в обиду Вам, но я удивлен, что в МФТИ не разбирают такие базовые вещи.
Это у теоретиков результат измерения — "конкретное число". А у нормальных людей измерение (любое измерение) обязано сопровождаться точностью измерения (ака «погрешность»).
Откройте любой справочник физических величин — каждая величина имеет точность (кроме трех-четырех настолько фундаментальных, что их решили по определению считать точно равными некоторым значениям).
(Заодно расскажите, на каких биржах торгуют «физическими величинами»...)
Ivan FXS, что-то беседа теряет смысл.
Цена — с ней вроде бы понятно. Хотя даже в этом вопросе часть исследователей сразу начнет брать логарифм от реальной наблюдаемой цены.
А такие вещи как дрейф (ака тренд), дисперсия (ака ашви), Херст и т.д. и т.п. — это все результат измерения. И этот результат имеет точность, которая обусловлена точностью той вычислительной процедуры, которой Вы пользуетесь.
Думаю, это будет лучше соответствовать тематике ресурса, чем ликбез по основам метрологии.
Базис можно брать любой, чем проще, тем лучше. Мне нравится веер EMA-шек, просто, дешево и сердито. И смысл понятен, так как это просто пачка фильтров нижних частот.
Какой базис ни возьми, от нестационарности всё равно никуда не убежишь ) самое интересное именно в том, как её бороть
Zweroboi, для сишарпа тоже есть крайне интересные математические библиотеки. Тот же АлгЛиб к примеру. Но это частности.
Тогда Вам по такой же схеме несложно запихать Фурье-разложение в алгоритмы самообучения. Если верить Николай Скриган там главная хитрость — чтобы центры полосовых фильтров отличались в 5 раз.
Zweroboi, =) в умелых руках, говорят, и ассемблер чудеса творит… Все сводится к наличию мат. библиотек насколько понимаю.
У меня к питону отвращение почти физическое. Хуже питона был только опыт с фортраном… =D
В ценовых рядах, акций, валют и т.п нет устойчивых циклов, нет устойчивых закономерностей. Существует огромное количество всяких методов фильтрации, но они, как их не экстраполируй, не являются достоверными прогнозами. Существует немалое количество методов предсказания временных рядов. Эти методы даже работают, но только в том случае, если во временном ряду есть закономерность. Её величество вероятность правит рынком.
А.Г. торгует системы, в которых базовая конструкция рынка следующая:
рынок колеблется вокруг константы, которая в случайный момент времени изменятся на другую константу. То есть, аппроксимация рынка кусочно-постоянными функциями. В чем отличие от Уолша в первую очередь, в том, что нет периодичности и нет константного шага по времени — время переключения случайно и непредсказуемо.
Гудылин выстраивает фракталы, вероятно вложенные. Я его не вполне понимаю, но конец и начало любого фрактала — локальный экстремум. Наверное, это похоже на аппроксимацию рынка ломаными.
SergeyJu, очень содержательное изложение. Это он сам так рассказывал?
Тогда по сути нам надо открывать монографию по исследованию процесса Орнштейна-Уленбека — и вперед. Заниматься подбором параметров на основании наблюдаемой истории процесса.
Sergey Pavlov, ночные гепы только увеличивают неконтролируемую дисперсию. Это снижает допустимое плечо и, следовательно, итоговую доходность.
Лучше интрадеить со сделкой +1 шаг цены, чем овернайтить и нервничать каждую ночь (выходные).
На рынке существует статистическая связь между шириной дипазона колебаний актива и длительностью интервала наблюдения. В первом приближении, ширина диапазона колебаний пропорциональна кв. корню из времени. Разложение по ортогональному базису неявно содержит предположение об периодичности процесса, что неверно для рынка. Вейвлеты, полосовые фильтры и наборы ЭСС обладают тем свойством, что различные их элементы имеют разные временные параметры усреднения. Соответственно, и разную глубину памяти о прошлом. Это не базисы в том смысле, как понимается в линейной алгебhе. Как могут образовывать базис вектора РАЗНОЙ ДЛИНЫ? Однако, я другого решения не вижу, как работать с такого рода неправильными базисами или вообще отказаться от базисов на основе временных фильтров типа свертки. А что у нас есть, не сводимое к свертке? Например, максимумы и минимумы, локальные экстремумы.
т.е. если предположить что есть робот, который методично вливает бабла, то его можно найти, но ведь наверняка это прячут.
более того, как я понимаю, спрятать могут так, что как говорится, и ты суслика не видишь, и я суслика не вижу, и цена не изменилась, но суслик уже вошел на всю котлету.
по объёму это ещё можно как-то увидеть.
но вы же объём не учитывали.
Стас Бржозовский, "линейный трейдинг — очень сложно. Проще разобраться с опционами".
Кстати, у меня видимо карма продавца: стоит что-то купить — и полный провал. =D И почему-то даже мысль об ограниченном убытке не греет.
1) купив линейным активом волатильность нужно ее где то потом продать. Без опционов приходится продавать тем же линейным активом. Соответственно, значительно сужаем возможности
2) года полтора уже как постоянно возникают возможности купить опционами волатильность очень дешево, относительно прогнозов (моих) rv. Линейным активом это сделать просто невозможно
3) за счет крымнашей и подобных дел возникают очень серьезные риски попасть на деньги локально при направленной трендовой торговле овернайт. В опционах можно эти риски убрать
4) торговля линейным активом не дает возможности заработать на календарях, перекосах улыбки и тому возможных вещах
5) торговля линейным активом почти не дает возможности заработать на сильных изменениях vol(vol)
и тд и тп
Вопрос же был в вашем утверждении, что с опционами проще. Вот и вопрос… так ли проще и за счет чего проще? Или это оказывается результатом индивидуальных предпочтений, которые для каждого индивида как-то случайно формируются?
Мне думается, что выбор инструментария для торговли (БА или опционы) это вопрос техники, а первичен всё равно БА, про который мы должны что-то спрогнозировать… направление, волатильность, границы, еще чего-нибудь… Или я не прав на ваш взгляд?
Sergey Pavlov, давате прямо с оснований начнём. Вот вы пишете:
«В качестве оценки естественности мы исходили из наивного допущения: что лучше работает, то и естественнее. Лучше — значит обладает лучшими прогнозными свойствами.»
— однако, что означает «работать» применительно к трейдингу? Разве «работа» трейдера состоит в том, чтобы «давать прогнозы», а не в том, чтобы совершать прибыльные (хорошо, прибыльные в среднем) сделки?
_
И что такое «правильный прогноз»? Прогноз «01.01.2019 цена нефти будет 100$ плюс-минус 90$» — он «правильный» или нет?