У каждой своя проблема:

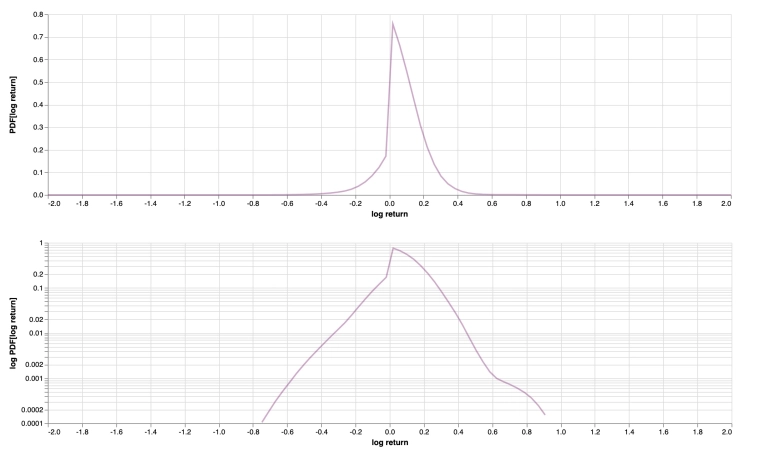
— PDF показывает плотность а не вероятности, нужно закрашивать полутонами площадь графика чтоб показать вероятности что не всегда удобно.
— PMF не стабильна при изменении шага дискретизации (см картинку ниже).
— CDF/SurvF на лог маштабе половину перекашивает.

Что использовать, для наглядности, чтоб показывало реальные вероятности, в том числе в лог маштабе? Как вариант комбинацию CDF: х<0, SurvF: х>0 (или можно выбрать моду/дреднее вместо 0).





Пример проблемы с PMF, PMF очень удобна и интуитивно понятна, но, имеет неприятную проблему, графики ниже одно и то же распределение, с разным шагом дискретизации, если его показать не точками а линией то вообще непонятно что это одно и то же.



( Читать дальше )

Он упомянул интересные моменты о фонде Медальен:

— Они не используют анализ финотчетности, а только анализ цен и других индикаторов.
— Тем не менее он считает анализ финотчетности рабочим подходом.
— Аномалии которые они используют небольшие (и в других интервью он упоминал что эти аномалии б) со временем исчезают в) поэтому требуется постоянный и ручной поиск новых и новых аномалий). Из этого следует (это уже мои мысли) поскольку аномалии маленькие, их требуется большое число, соотв. это высокочастотный трейдинга с огромным числом сделок, и наверняка скоростными каналами и льготными комиссиями, что недоступно обычным трейдерам.
— Огромные данные и вычисл мощности. В другом интервью 10 лет назд, Robert J Frey бывший глава исследований Медальен упоминал что каждый день Медальен получает и сохраняет порядка нескольких терабайтов (если не ошибаюсь) новых данных.  И в других интервью Джим Симонс также упоминал что они постарались получить все данные до которых только можно дотянуться, в том числе настолько старые насколько возможно, в ранние дни даже во время посещения какой то гос конторы вручную срисовав некий висящий та график со старыми данные.

( Читать дальше )

Смотрим типовой опцион «MSFT ПУТ, 6мес, страйк 0.8 ($310)»





Премиум, спред 8.25-8.60, середина 8.42. Середина это наиболее вероятная цена за которую удастся купить/продать.

Расчитаем какие максимальные потери мы можем понести, отдав прибыль кому то, кто делает арбитраж. Мы можем потерять максимум половину спреда (8.60-8.25)/2 = 0.175. Относительно премиума это будет 0.175/8.42=0.02 или — максимум -2% мы отдаем кому то другому.

Насколько это значительно? Для высокочастотной стратегии может быть значительно. Но, если стратегия долгосрочная, опцион покупается/продается на месяцы/годы, и его цена будет колебаться от 0 до 1000%, возможные потери на арбитраж -2%, это мизер.

Также, оценка потерь на арбитраж -2% завышена, в нее входит и арбитраж и спред (без спреда купить не удастся в любом случае), поэтому чисто на арбитраж потери даже меньше -2%.

Должна быть ликвидность, опционы MSFT ликвидны и 0.8 это близкий к текущей цене уровень где высокая ликвидность. На неликвидных акциях, особенно на далеких OTM опционах, спред может сильно расти, на совсем неликвидных вообще может не быть спреда и лишь пара заявок. Эти случаи могут быть опасными, и потери большими.

( Читать дальше )

Для Интела  «пут 360дней, страйк 0.8»: расчетная цена премиума европейский опцион 0.042, американский опцион 0.077. (текущая цена акции принята за 1, все параметры и относительно этой единицы).

Разница значительная. Волатильность в расчетах берется из прошлых периодов.

И, рассчитанные цены путов, как американских опционов, стали близкими к рыночным, но чуть меньше. Я собирался принудительно добавить в расчеты вероятность банкротства компании (как вероятность 1%/год падения до 1/10), думаю после этого расчетные цены путов станут практически равными рыночным.

Сравним 3 распределения вероятностей (ps), описывающие изменениe цены акции (xs)

xs: [x0.1, x0.5, х1.0, х2.0, x10 ] изменение цены

ps: [0.01, 0.05, 0.88, 0.05, 0.01] настоящее
ps: [0.00, 0.06, 0.88, 0.06, 0.00] кандидат 'a', мера КС = 0.01
ps: [0.01, 0.06, 0.86, 0.06, 0.01] кандидат 'b', мера КС = 0.02

Колмогоров Смирнов выберет 'а'. И можно представить какие это даст последствия — например прибыль по OTM опционам.

Альтернативы:

— Андерсон Дарлинг, но оно нестабильно и использовать его для эмпирических данных не получится.
— Макс относительная ошибка частот по квантилям. Стабильна, но менее точная.
— Макс относительняя ошибка частот по PMS/Histogram. Дискретная версия Андерсон Дарлинг, стабильность чуть ниже чем у квантилей, но точность чуть выше.

Цена AMD во времени в лог пространстве (log returns). С вероятностями в момент времени t (черные точки) и условными вероятностями переходов (синие линии).

Если посмотреть на черные точки детальней то это будет распределение имеющее форму



( Читать дальше )

Угадать где будет золотая жила, какие компании ИИ выведет в лидеры — нельзя, но можно продавать лопаты золотоискателям. 



В ближайшие 5 лет ИИ затронет рынок, по крайней мере его часть. Одни компании и акции уйдут вниз, другие вверх. Угадать технологических лидеров, изобретет новый чип Intel или TSM или литография ASML станет глобальным монополистом или наоборот станет ненужной из за новых способов? Угадать это нельзя.

Что будет лопатами для ИИ? Мне видится:

— Материалы: медь, серебро, редкоземельные материалы. 
— Энергия: нефть, газ, уран, электричество.

Как продавать лопаты?

Нельзя предсказать время, лопаты могут потребоваться через полгода, а могут через 5 лет. Второй момент, рост будет взрывным, из 10 секторов, один взлетит в х20 остальные х2. Угадать что взлетит в х20 мы не можем, соотв. ставка должна быть широкой, затрагивать и нефть и уран и материалы.

— Купить акции. Вариант, но мы сможем увеличить состояние лишь в х2 разa (скажем 1/10 капитала взлетела в х20 раз, 9/10 в 2 раза, в сумме получилось не так уж и сильно).

( Читать дальше )

Симуляция лог доходности акции как процесс проходящий в N заданных точках через заданные распределения. Дискретная аппроксимация случ. процесса, как граф условных вероятностей (серия матриц переходов, условных вероятностей). 


Группы синих точек — исходные вероятности в разные периоды времени. Черные линии — условные вероятности переходов.

В увеличенном виде:


( Читать дальше )

Чтобы оценить его уровень не нужно формул и мнений экспертов. Поскольку Мозг и ИИ это гибкие и универсальные машины, их уровень примерно одинаков во всех областях, и достаточно оценить пару чтобы сделать вывод об остальных.

Что значит гибкость и универсальность? Любой человек (за исключением нескольких процентов больных несчастных людей) имеет средние способности в любой области. Любой слесарь и тракторист может рисовать и решать задачи физики (если дать ему несколько лет и за ошибки бить палкой). Великим художником и ученым он не станет, но на хорошем уровне научится делать и то и другое.

Так и ИИ. Это облегчает задачу оценки уровня ИИ, нам не нужно давать ему сотни тестов, мы можем за секунду, без всяких тестов оценить его общий уровень глянув лишь одну область — видео.

Бывает что одна или другая область отстают, например текст долгое время отставал от картинок, но в течении пары тройки лет они обычно выравниваются. 

Выберем область в которой мы все эксперты — видео, и оценим уровень ИИ:

( Читать дальше )

Избежать потерь полностью нельзя. Но можно выбрать какими будут потери. Это правило позволяет превратить непредсказуемые, неизмеряемые и неограниченные потери — в потери предсказуемые, измеряемые и ограниченные. 

Правило которое нельзя нарушать — потеря больше 20% капитала в год.

Ограничение должно быть механическим, гарантированным. Не зависеть от расчетов, вероятностей, корреляций и аномалий. Соотв. диверсификации, теории портфелей, стоп лоссы (проскальзывания) не подходят. Риск нейтральные лонг/шорт зависят от корреляций и могут дать непредсказуемый результат, тоже не подходят. Слишком сложные стратегии с опционами тоже не подходят, в них можно ошибиться.

Я знаю 2 способа это сделать.

а) Ограничение рабочего капитала. Не вносить на рынок больше 20% капитала в год, минус что 80% будет лежать без дела.

б) Защита опционами. Гарантированная, от всех возможных движений рынка дающих >20% убытка. Например страховка пут опционами. Минус каждый год будут невозвратные расходы ~2-3% на страховку.

( Читать дальше )