Kot_Begemot
Нейронные сети и ученье о данных
- 22 февраля 2020, 22:12
- |
Когда вы занимаетесь искусственным интеллектом, то вам и в голову не приходит использовать нейронные сети! Да… такова их внутренняя сущность — к интеллекту они не имеют ровным счётом никакого отношения. В своё время NN (нейронные сети, Neural Networks) прочно ассоциировались со спиновыми стёклами — аналогом магнитной плёнки — на которую при желании можно записать ту или иную информацию. Да… в то время ещё не было ученых… как бы это правильнее перевести… ученых по данным… и в литературе часто можно было встретить выражение «образец, хранящийся в памяти сети». Другими словами, с самого своего рождения нейронные сети ассоциировались совершенно не с интеллектом, а с обычным хранилищем, своеобразной библиотекой.
Всё «обучение» нейронной сети, в те времена, сводилось к тому, чтобы загрузить в её память наиболее репрезентативную выборку образцов, чтобы с ней, в конце-концов, не случилось конфуза и она не смогла бы с завидной регулярностью идентифицировать афроамериканцев как горилл, как это случилось у Data Scientist'ов из Google Photos. Поэтому, помимо школьной алгебры мы, как квалифицированные специалисты, изучали ещё и прикладной предмет, чтобы в любой момент, когда практика не согласовывалась бы с теорией, отметать… практику.
( Читать дальше )
- комментировать
- ★5
- Комментарии ( 36 )
Теория и Практика Дельта-Хеджа
- 26 января 2020, 12:41
- |
Для того, чтобы продать волатильность, нам необходимо продать стрэддл — этим, мы полностью избавляемся от чувствительности к направлению движения цены, оставляя при этом чувствительность к «волатильности»… Чтобы не запутаться, обозначим первую волатильность за IV (Implied Volatility) и будем считать её заранее известной и эффективной.
Если бы рынок был монеткой и выходил бы на экспирацию двумя возможными вариантами {+IV, -IV }, то результатом продажи нашей опционной конструкции был бы ровно 0, в силу равенства IV=RV. Но рынок выходит на экспирацию через «тренды» и «пилы», которые выводят Базовый Актив в том числе далеко за ± IV, и в том числе и в ноль. В результате, конечное отклонение от ± IV и, соответственно, риски, которые мы принимаем при продаже стрэддла, составляют приблизительно :
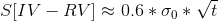
где S — СКО, RV ( «реализованная волатильность») - отклонение цены на экспирацию, t — время до экспирации, а сигма0 — величина шага движения цены. Это уравнение можно получить численно, а можно, взяв интеграл по соответствующему распределению Гаусса (аналитический вариант).
( Читать дальше )
Дельта Хеджирование и Компрессия рисков
- 23 января 2020, 22:31
- |
Каждый учебник предлагает нам простой и эффективный метод извлечения прибыли — репликация опциона при помощи фьючерса. При чем все, что для этого нужно — всего лишь «не думать и торговать по принципу: растёт — покупай, падает — продавай!». Всё просто, понятно, бесспорно и… совершенно неверно.
Потому что «не думать» — в процессе погони за прибылью, — на самом деле, сложно. И если вам непонятно, зачем вообще нужны эти опционы, если они так легко реплицируются фьючерсами, то просто брать, и «не думать», уже не получается. Не думать хорошо после того как вы уже хорошо подумали, и думать второй раз — как минимум, лень. А с первого раза вообще мало чего получается. Особенно — не думать.
Так бы и закончилось моё дельта-хеджирование не начавшись, если бы оно не было столь модным. А то ещё всякое бывает — не задельта-хеджируешь, а потом скажут, что вот, дескать, «Пастернака не читал, но действия его уже осуждает». Нет, надо всё таки разок попробовать… А то в приличном обществе ещё и засмеют почём зря.
( Читать дальше )
Критерий Келли через нормальное распределение
- 20 января 2020, 21:27
- |
Ещё до того как я познакомился с критерием Келли, я уже успел наработать собственную широкую базу риск-оценок. И вопрос отказа от этого критерия для меня был, по сути, риторическим, тем более, что Келли, как бы мы того не хотели, достаточно примитивный (упрощённый) критерий. Но прежде чем отказываться от критерия хорошо бы вообще понять что это такое, учитывая, что критерий представляет весьма простое решение сложной задачи и интересен именно этим.
Для примера возьмём игру с нулевым E, в которой выигрыши распределены равномерно, с вероятностью 50/50 и представлены множеством {+50%,-50%}. За некоторое количество повторений, например за два раунда, мы будем иметь следующее распределение финансового результата:
- 25% случаев — выигрыш 125% капитала до 2.25 (два выигрыша подряд)
- 25% случаев — проигрыш 75% капитала до 0.25 (два проигрыша подряд)
- 50% случаев — проигрыш 25% до 0.75 (один выигрыш и один проигрыш)
Рассчитав статистические моменты этого распределения легко убедиться, что средний выигрыш, как это положено, будет равен нулю, а наиболее вероятный вариант (мода) будет представлен проигрышем 25% капитала. Теперь, если варьировать ставку, можно убедиться, что с ростом ставки математическое ожидание по крайней мере не снижается, а мода, то есть наиболее вероятный исход — падает.
( Читать дальше )
Как я провёл этим летом
- 03 января 2020, 13:04
- |

Иллюстрация кибернетического Бога.
И от этого унылого однообразия, в конце-концов, спасает только пафос, превозносящий обычные сортировочные алгоритмы, годные только на расстановку ссылок в архивах Яндекса и Гугла и составления коллекций изображений котиков, до уровня каких-то божественных проявлений — искусственного интеллекта, машинного обучения, автопилотов, роботов и пр. И дабы не обидеть серых ботанов, умеющих сложить 2 и 2 тремя тысячами абсолютно одинаковых способов, мы называем их гордо Data-scientist'ами, Research-Manager'ами at Information Technologies Companies, Quantitive CEO'S, и ещё какими-нибудь оскорбительными непонятными словами.
( Читать дальше )
Язык дракона и танец волатильности
- 02 декабря 2019, 01:43
- |

«Настоящее образование включает умение хорошо петь и танцевать». Платон.
Коллега ch5oh задал парадоксальный, на первый взгляд, вопрос: «как продавая дорого то, что стоит дешево, можно ещё и умудриться проиграть?»
Однако парадоксально он выглядит лишь до тех пор, пока мы остаёмся в рамках косной метафизики, не желающей, и не склонной к диалектическому танцу.
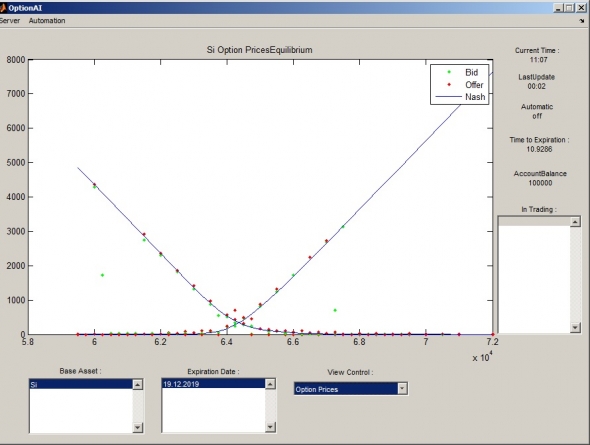
Для сравнения этих двух подходов — метафизики и диалектики — мы будем рассчитывать Нэш-равновесные цены двух недельных опционов (STO) и моделировать игру покупателя и продавца. В первом случае мы будем исходить из постоянства (авторегрессии) волатильности, пользуясь исключительно текущей HV, а во втором — из её танца (mean-reverse AR), о котором, как нам кажется, мы знаем чуть более, чем ничего.
* То, что волатильность представляет из себя mean-reverse процесс, подобный движению Орнштейн-Уленбека, неоднократно было показано Дмитрием Новиковым ,
( Читать дальше )
О покерных игроках и опционах
- 23 ноября 2019, 21:05
- |
Опцион (OTM) — это такое флэш-дро: сам по себе он не имеет никакой ценности (внутренней стоимости), но даёт вам право выиграть банк, если будущие выпавшие карты, составляющие элемент случайности, дополнят ваше дро (draw), до полной комбинации. Вы платите за дополнительные карты, отдаете временную стоимость оппоненту — владельцу готового фьючерса (внутренней стоимости), и, в случае удачи, выигрываете банк.

Как ни странно, но все игроки в покер начинают изучать азы с волатильности, считая вероятность, с которой OTM-дро станет ITM — флэшом и выйдет в деньги. Для этого даже придумываются специальные калькуляторы, рассчитывающие EV (средний поток выигрышей) на основе Pot-Odds (вероятность исполнения флэш-дро в деньгах), моделируемые методом Монте-Карло и формулой Блэка-Шоулза.
Самые продвинутые игроки, конечно, уже не используют HV и Pot-Odds, заменяя их на IV и Implied Odds, потому что знают, что существует tail-effect и leverage-effect и часто, после собирания готового флэша из дро, владельцы фьючерсов умудряются ещё несколько раз накуконить в банк до вскрытия (Expiration), фактически (!) раздаривая деньги. Так, например, на вышеприведённой картинке вполне оправдана покупка опциона (Call) для красного игрока.
( Читать дальше )
COM интерфейс МаtLab в LUA
- 19 ноября 2019, 12:10
- |
Естественно, сразу возникла необходимость передать полный контроль над этим двумя сложнейшими приложениями чему-то более простому и понятному, например Матлабу, чтобы нажимая разноцветные кнопочки «Обыграть рынок» и «Что там опять у волатильности?» оставить конечному пользователю, то есть мне, только наслаждение от наблюдения за происходящим.
Теоретически, для этого надо нанять менеджера COM из LUACOM.dll и дать ему в управление пару простых исполнителей — объектов LUA, чтобы высшее руководство МатЛаба могло эффективно распоряжаться ресурсами в иерархии
Руководство МатЛаб -> менеджер интерфейса COM -> исполнитель объект LUA
Но в силу каких-то неведомых причин (от сборки dll, до сборки MS Windows и даже предустановленного железа) сделать по теории управления с ходу не получилось, поэтому была использована альтернативная схема:
( Читать дальше )
Контроль рисков в играх с рекапитализацией
- 04 ноября 2019, 20:28
- |
Сложность задачи контроля рисков состоит в том, что риски в действительности не ограничены и нарастают с течением времени так, что превращают бесконечно длительные игры с полной рекапитализацией в игры с абсолютно неконтролируемым риском. В связи с чем, задача выбора оптимального плеча (объёма) становится в общем случае математически не решаемой, а риск-менеджмент, в конечном счете, определяется только психологическим комфортом управляющего или инвестора. Тем не менее, исходя из некоторых предпосылок мы можем ограничить зону допустимого психологического комфорта и склонности к риску, то есть указать на некоторые их разумные пределы.
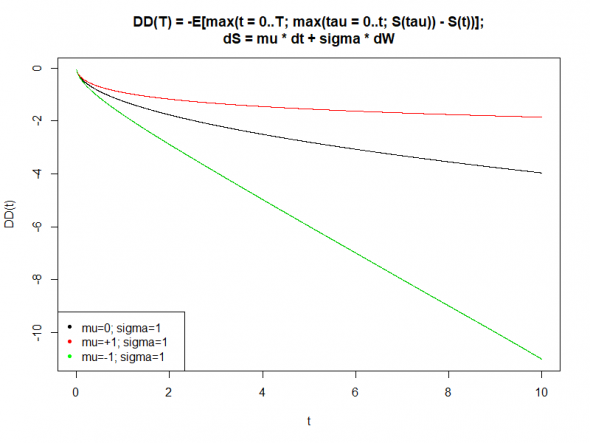
Изображение зависимости средней ожидаемой максимальной просадки заданных стратегий от времени. Любезно позаимствовано у Eugene Logunov.
Как и ранее, имея стартовый капитал 50 млн. долларов США мы будем пытаться обыграть господина Баффета, имеющего 500 млрд. долларов США, то есть будем стараться увеличить свой капитал в 10 000 раз за счёт игры на бирже. Играть мы будем нелинейно, то есть будем увеличивать ставки после каждого удвоения пропорционально текущему капиталу и поэтому для реализации нашей цели нам предстоит выиграть у господина Баффета не 10 000 раз подряд, а всего лишь:
Мы знаем, что наша стратегия обладает преимуществом над стратегией господина Баффета и позволяет играть против него с вероятностью 55%/45%, то есть с 10% смещением (Шарп = 1.6)
( Читать дальше )
теги блога Kot_Begemot
- API
- cpp
- FORTS
- LUA
- Matlab
- NASDAQ
- open source
- Quik Lua
- S&P
- S&P500
- S&P500 фьючерс
- Vanguard Group
- VIX
- акции
- акции США
- алгоритмы
- алготрейдинг
- анализ временных рядов
- баффет
- волатильность
- Гордон
- доверительное управление
- долги
- игры
- инвестиции
- индекc
- интеграция
- искусственный интеллект
- Келли
- Книги
- книги о трейдинге
- корреляция
- кризис
- криптовалюта
- лудомания
- Марковиц
- матлаб
- машинное обучение
- ММВБ Акции
- наука
- нейронные сети
- облигации
- одураченные случайностью
- оптимизация
- оптимизация торговых систем
- опционы
- оффтоп
- оционы
- памм счета инвестиции
- паника
- пирамида
- ПИФы
- портфели
- Портфель
- портфельное инвестирование
- пузыри
- раздача
- рецензия
- Риски
- рэнкинг мосбиржи
- Сбербанк
- спекуляции
- статистика
- стоимостное инвестирование
- талеб
- теги не нужны
- теория игр
- торговая система
- торговые роботы
- трейдинг
- улыбка волатильности
- управляющая компания
- финанализ
- фундаментальный анализ
- фьючерс ртс
- Шарп
- шутка
- Экономика