Блог им. uralpro |Оптимальные стратегии возврата к среднему. Часть 2
- 26 марта 2017, 14:03
- |
Продолжение. Начало здесь.
2.3. Расчет показателей
Для каждой пары мы рассчитываем пять показателей в тренировочном и проверочном периодах, а именно годовую прибыль, коэффициент Шарпа, среднее время сделки, приведенную к году частоту сделок, и прибыль за сделку.
Дневную прибыль рассчитаем следующим образом:
( Читать дальше )
- комментировать
- ★12
- Комментарии ( 10 )
Блог им. uralpro |ADF тест для парного трейдинга в Excel
- 17 сентября 2016, 12:23
- |
Полезная статья с сайта www.quantinsti.com о тесте на коинтеграцию, применяемому в парном трейдинге.
Как вы знаете, для реализации стратегии парного трейдинга необходимо проведение тестов на коинтеграцию используемых инструментов, и для этой цели часто применяют дополненный тест Дики-Фулера (ADF). Тем не менее, при поиске критериев коинтеграции, ADF не стоит в первых рядах. Скорее, его можно найти по запросу «тестирование на единичный корень (unit root)».
Казалось бы, легко взять книгу по временным сериям и научиться ADF, но эта задача на деле не так проста.Необходимо прочитать не менее 6 глав об анализе временных серий перед тем, как понять различные способы применения ADF в контексте статистического арбитража.
Если вы хотите изучить тест подробно, то прочитайте статью по следующей ссылке: http://robotwealth.com/exploring-mean-reversion-and-cointegration-part-2/
( Читать дальше )
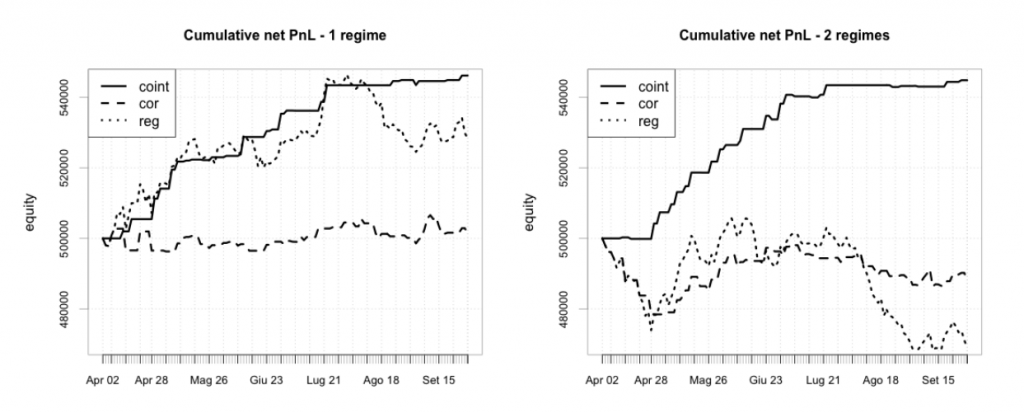
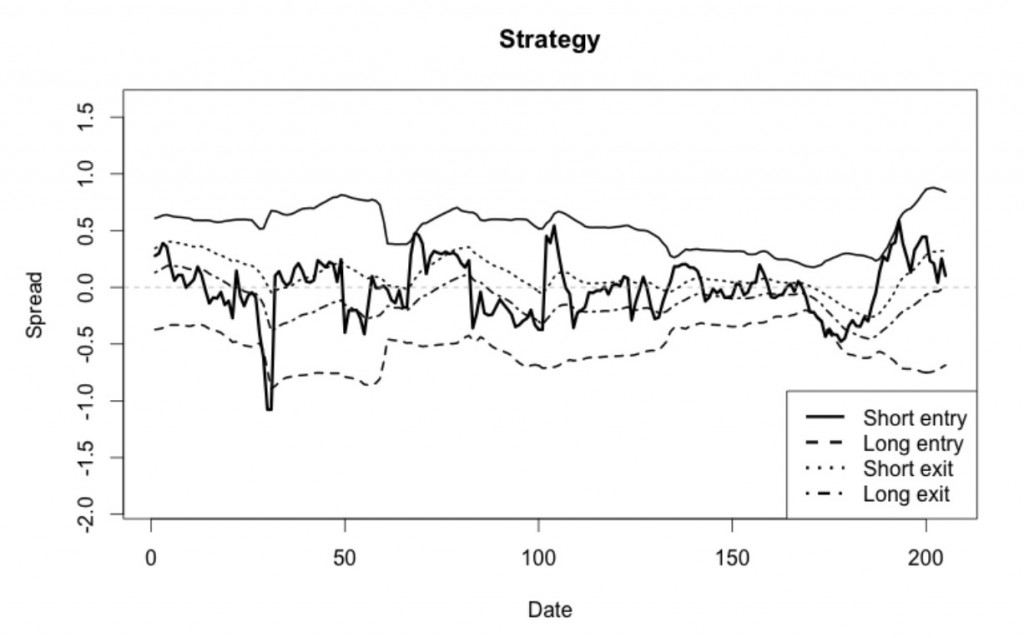
Блог им. uralpro |Парный трейдинг с переключением режимов. Часть 3
- 07 октября 2015, 09:03
- |
Окончание. Начало здесь.
В соответствии со смоделированным спредом, мы предполагаем покупать (продавать) пять контрактов по одному активу, одновременно продавая (покупая) количество, равное [β×5], где [x] — целая часть х, по другому активу, так как число контрактов должно быть целым.
Мы моделируем торговлю с 500 000$ и наше гарантийное обеспечение будет примерно равным 20%. Мы не используем какую-либо технику манименеджмента, ГО 20% будет только в начале периода бэктестинга и будет снижаться по мере получения прибыли.
Итоговые результаты анализируются с помощью распространенных индикаторов, применяемых на практике: годовой коэффициент Шарпа, годовая доходность, максимальная просадка, доли дней с положительной и отрицательной доходностью, доля дней без сделок, коэффициент отношения среднего значения (в долларах) дней с положительной доходностью к дням с отрицательной доходностью, корреляция портфеля с индексом S&P500. Во всех случаях мы указываем чистый результат, принимая во внимание 3$ комиссии и один тик проскальзывания на сделку.
( Читать дальше )
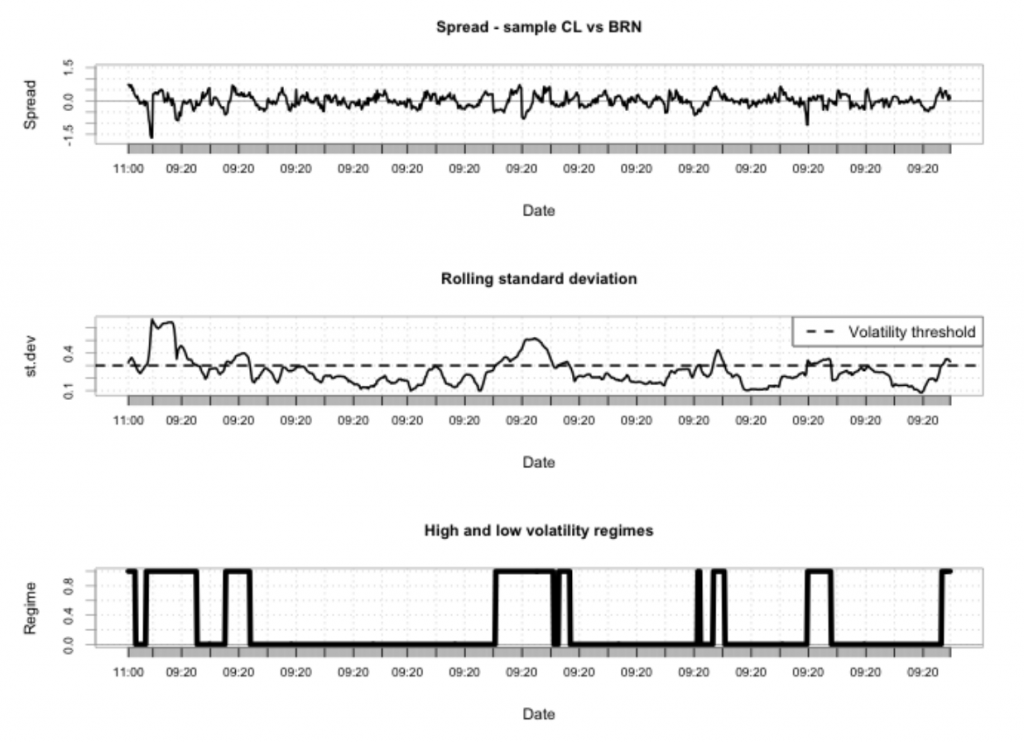
Блог им. uralpro |Парный трейдинг с переключением режимов. Часть 2
- 29 сентября 2015, 08:58
- |
Продолжение. Начало здесь.
Модель, устойчивая к смене режимов волатильности
Некоторые проблемы торговли спредом
Ранее мы определили три сосотавляющих рыночно-нейтральных стратегий. Здесь мы обновим эту классификацию и рассмотрим некоторые трудности, связвнные с торговлей спредом.
Долговременные расхождения в ценах трудно найти с помощью алгоритмов, основанных только на ценах. Обычно, фундаментальный анализ, совместно с опытом трейдера может помочь в понимании существования расхождения. Время возврата к среднему может быть установлено с помощью непрерывных моделей, в этом случае период удержания позиции зависит от модели спреда и, следовательно, от частоты пересчета коэффициента хэджирования.
Много факторов могут приводить к скачкам волатильности спреда, но сами по себе скачки не могут быть приняты в качестве сигналов прекращения торговли парой.
( Читать дальше )
Блог им. uralpro |Парный трейдинг с переключением режимов. Часть 1
- 16 сентября 2015, 09:04
- |
По итогам последнего голосования на моем сайте победила статья Marco Bee University of Trento — Department of Economics and Management,Giulio Gatti ,Università degli Studi di Trento — Department of Economics and Management — An Improved Pairs Trading Strategy Based on Switching Regime Volatility (Улучшенная стратегия парного трейдинга, основанная на переключении режимов волатильности). Ниже привожу перевод ее основных глав.
Введение
Стратегия, основанная на рыночно-нейтральном подходе, подразумевает, что трейдер должен принять три основные решения:
- Выбрать активы для торговли из набора множества торгуемых инструментов
- При существующем спреде ( т.е. динамически взвешенной разнице между двумя активами) определить его смысл в соответствующих эконометрических терминах
- Выбрать торговый алгоритм
( Читать дальше )
Блог им. uralpro |Алготорговля коинтегрированными активами. Часть 1
- 27 августа 2015, 12:37
- |
Итак, по результатам голосования на моем сайте в лидерах оказалась публикация Alvaro Cartea и Sebastian Jaimungal "Algorithmic Trading of Co-integrated Assets". Я тоже считаю эту работу очень интересной, так как она фактически расширяет понятие парного трейдинга до торговли произвольным количеством активов, с учетом их коинтеграционного взаимоотношения. Это сильно повышает устойчивость результирующего портфеля, в отличие от парного трейдинга, в связи с его диверсификацией.
Представляю здесь перевод этой статьи, которую я несколько сократил, убрав длинные математические выкладки и оставив только наиболее важные и окончательные формулировки. Думаю, это значительно облегчит понимание, без утраты основного смысла публикации.
Вступление
Успех многих торговых алгоритмов зависит от качества предсказаний движения цены актива. Предсказания цены отдельной акции в общем случае менее точно, чем предсказание значения портфеля активов. Классической стратегией, которая использует совместное поведение двух активов, является парный трейдинг, где портфель состоит из линейной комбинации этих активов. Для примера, это могут быть две акции, чей спред, представляющий собой разницу их цен, демонстрирует особый паттерн, отклонения от которого носят временный характер. Алгоритм парного трейдинга получает прибыль от ставки на тот факт, что отклонения спреда возвратятся к их историческому или предсказуемому уровню.
( Читать дальше )
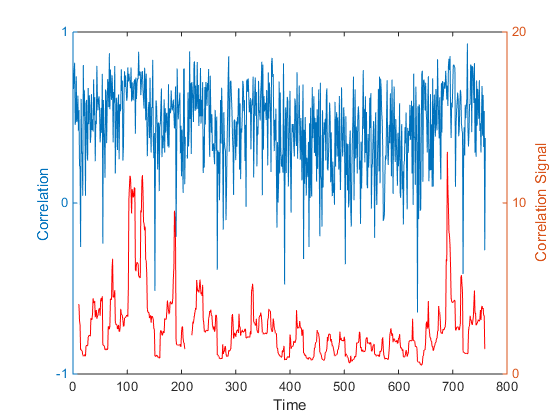
Блог им. uralpro |Корреляционный сигнал
- 31 июля 2015, 09:01
- |
Использование корелляции широко распространено в финансовой теории и практике, от создания портфелей до стратегий статистического арбитража.
Основная сложность в применении корелляции это ее изменчивость: активы, которые в один момент времени кажутся практически некоррелироваными для целей хеджирования, могут стать высококореллироваными в другие моменты времени, например, при высокой активности рынка. Напротив, акции, кажущиеся подходящими для парной торговли, в связи с высокой корелляцией их приращений цены, могут позднее показать разнонаправленную динамику, приводящую к значительным потерям.
Нестабильность уровня еще усугубляется эмпирическими выводами о том, что волатильность корреляции сама по себе зависит от времени: в одно время корреляция между активами может плавно меняться в узком диапазоне, в другое время мы можем наблюдать изменения знака коэффициента корелляции в течении нескольких дней.
( Читать дальше )
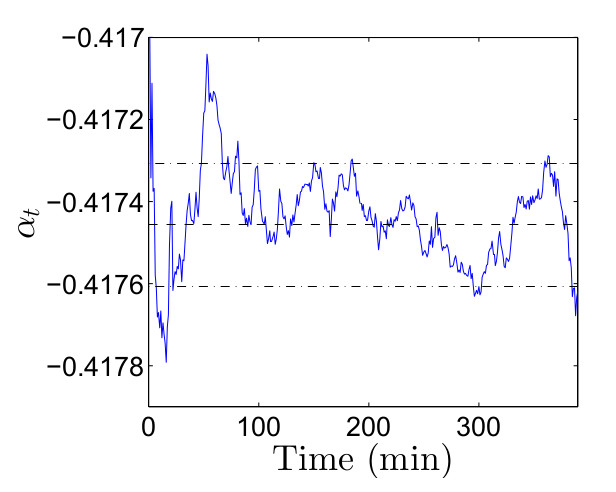
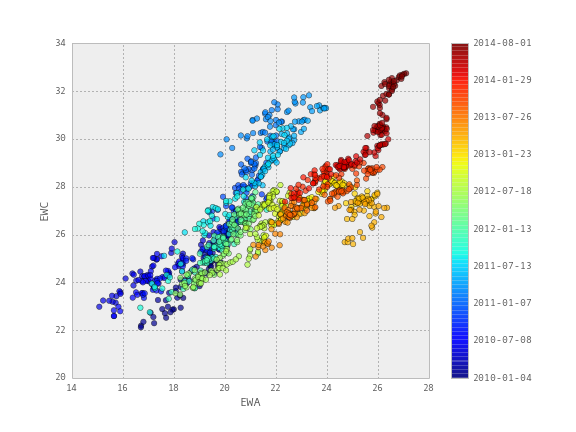
Блог им. uralpro |Линейная регрессия с использованием фильтра Калмана
- 23 апреля 2015, 10:12
- |
Линейная регрессия часто используется для вычисления пропорции хеджирования в парном трейдинге. В идеальной ситуации коэффициенты этой регрессии — наклон линии регрессии и свободный член (пересечение) остаются всегда постоянными. Однако в реальности все, конечно, не так радужно, и значения этих параметров постоянно меняются во времени. Как правильно вычислять коэффициенты регрессии, чтобы избежать подгонки к текущей ситуации, рассматривается в статье "Online Linear Regression using a Kalman Filter". Для этой цели в данной публикации используется фильтр Калмана.
Для тестирования берутся исторические цены закрытия двух биржевых фондов ETF — австралийского EWA и канадского EWC с 2010 по 2014 год. Динамика цен этих фондов показывает взаимосвязь, что продемонстрировано на диаграмме рассеивания в заглавии поста. Однако по этому же графику видно, что эту взаимосвязь невозможно описать с помощью линейной регрессии с постоянными коэффициентами.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс