Блог им. uralpro |Простое преимущество в SPY
- 13 августа 2016, 09:00
- |
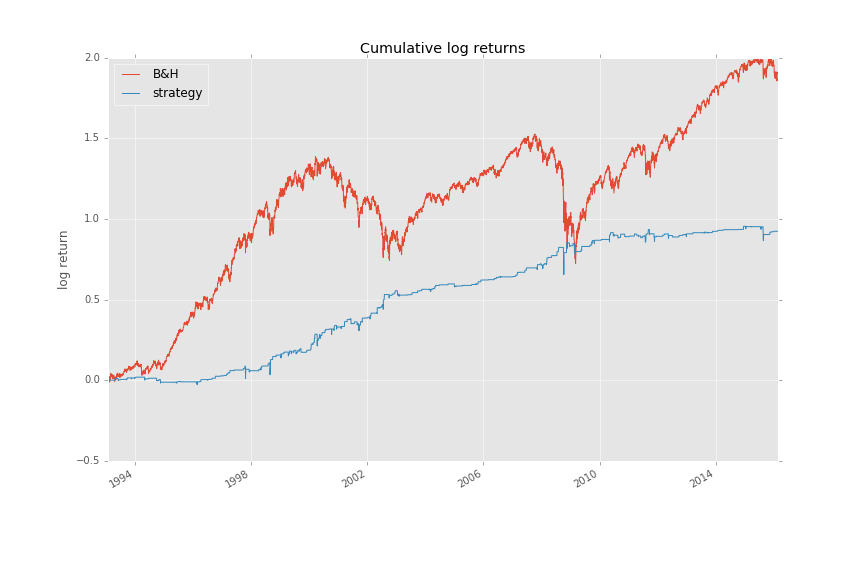
Статья из блога "Trading with Python" об элементарной стратегии, которая демонстрирует последовательный подход к разработке алгоритмов.
Недавно я прочел пост на сайте turingfinance.com "Как стать квантом". Вкратце, он описывает научный подход к созданию торговых стратегий. Для меня, наблюдение за данными, обдумывание модели и формирование гипотезы является второй натурой, как это и должно быть для любого хорошего инженера.
В данной статье я собираюсь показать такой подход по шагам, которые нужны для разработки стратегии.
Давайте возьмем наиболее популярный инструмент — S&P 500 ETF «SPY». Начнем с наблюдений.
Обзор данных
Мне кажется, что большую часть времени в СМИ говорят об обрушении рынков (больших потерь в течение нескольких дней), умалчивая о значительном росте, который следует за ними.
( Читать дальше )
- комментировать
- ★20
- Комментарии ( 7 )
Блог им. uralpro |Путеводитель по разработке биржевых роботов-2
- 11 августа 2015, 09:06
- |
Продолжение. Начало здесь.
После того, как стратегия протестирована и, насколько это возможно, избавлена от недооценки/подгонки, с хорошим коэффициентом Шарпа и минимизированными просадками, настало время выстроить систему исполнения.
Система исполнения ордеров
Система исполнения отвечает за то, каким образом список сделок, сгенерированных стратегией, отправляется и исполняется на стороне биржи. Несмотря на тот факт, что генерация сделок может быть полу- или полностью автоматической, механизм исполнения может быть ручным, полуавтоматическим или полностью автоматическим. Для LFT стратегий ручное или полуавтоматическое исполнение применяется наиболее часто. Для HFT алгоритмов необходимо создать полностью автоматический механизм исполнения, который скорее всего будет тесно интегрирован с генератором сделок (из-за сильной зависимости стратегии и технологии).
( Читать дальше )
Блог им. uralpro |Волатильность как актив-1
- 24 июля 2015, 09:28
- |
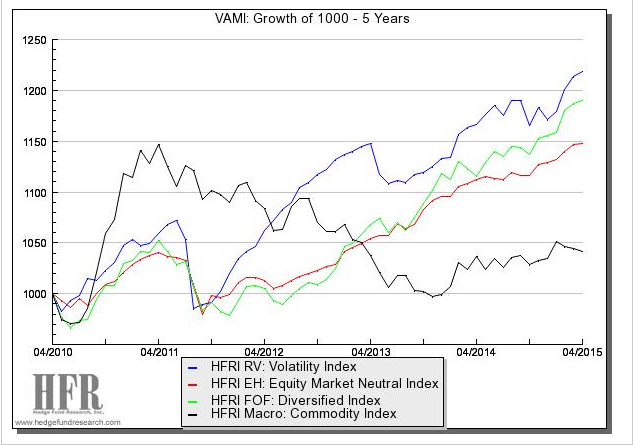
Объем торговли волатильностью как активом растет уже более 15 лет. Основные принципы и понятия этого процесса изложены в блоге QUANTITATIVE RESEARCH AND TRADING .
В последние годы стратегии торговли волатильностью показывают производительность значительно большую, чем глобальные индексы и дивесифицированные фонды фондов ( см. график в заглавии).
Основные понятия
Волатильность ненаблюдаема
Волатильность это особый дериватив, справедливая цена которого никогда не будет известна, даже после значимого события она, по сути, ненаблюдаема. Вы можете установить, что волатильность актива на протяжении некоторого исторического периода, например, равна стандартному среднеквадратичному отклонению приращений цены. Но это только оценка, одна из множества подходов, которые имеют свои недостатки. Сейчас мы знаем, что волатильность может измерена с почти произвольной точностью с использованием оценки интегральной волатильности ( по существу, метрики, основанной на высокочастотных данных), но это не изменяет тот факт, что наше знание о волатильности всегда неопределенно, в отличие от цены, например.
( Читать дальше )
Блог им. uralpro |Измерение токсичности потока ордеров. VPIN для HFT. Часть 4
- 16 июля 2015, 09:21
- |
Начало в моем блоге.
Условные вероятности
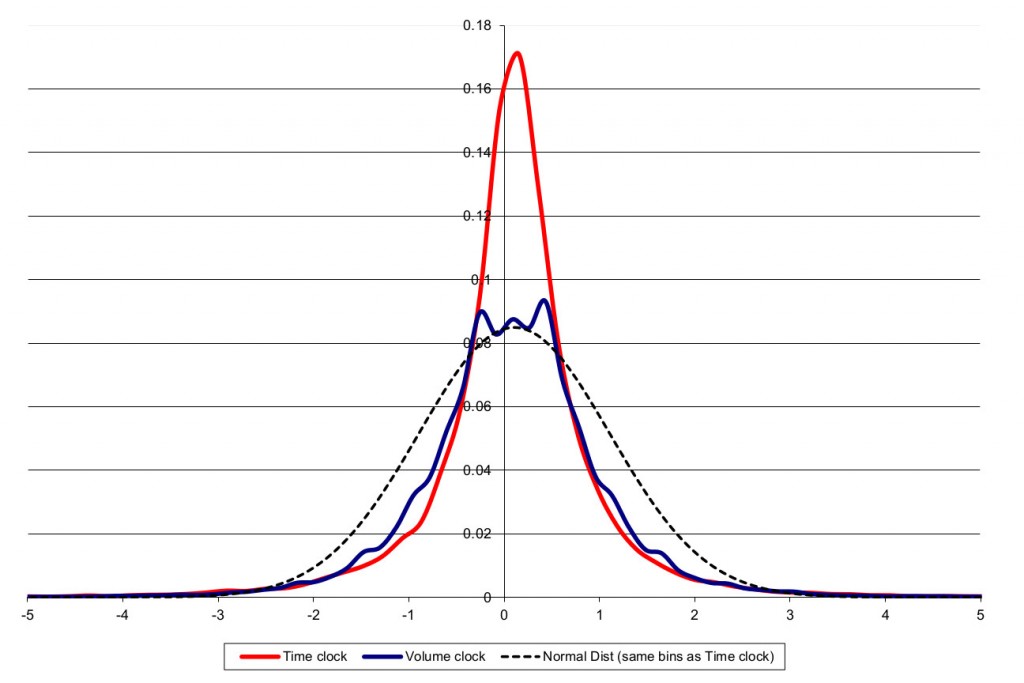
Для получения условных вероятностей, упомянутых нами в конце части 3, нужно вычислить совместное распределение VPIN и абсолютных приращений. Для этого сгруппируем VPINы c 5% шагом и абсолютные приращения в отрезки по 0,25%, чтобы отобразить дискретные распределения. Затем получим совместное распределение (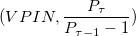 ). Из этого совместного распределения выведем два распредения условной вероятности.
). Из этого совместного распределения выведем два распредения условной вероятности.
( Читать дальше )
Блог им. uralpro |Измерение токсичности потока ордеров. VPIN для HFT. Часть 3
- 13 июля 2015, 15:08
- |
Начало в моем блоге.
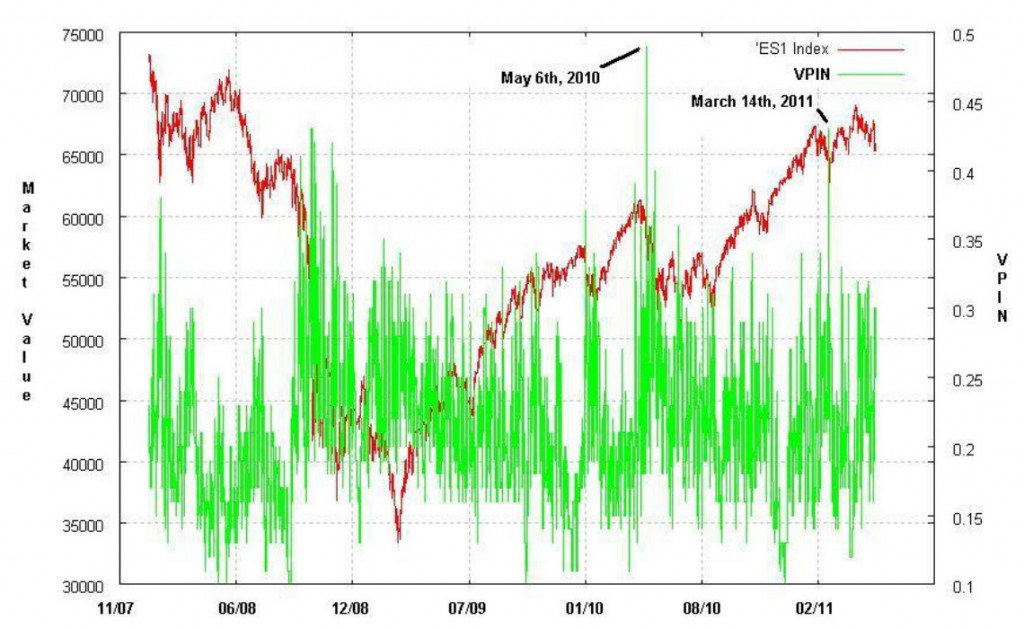
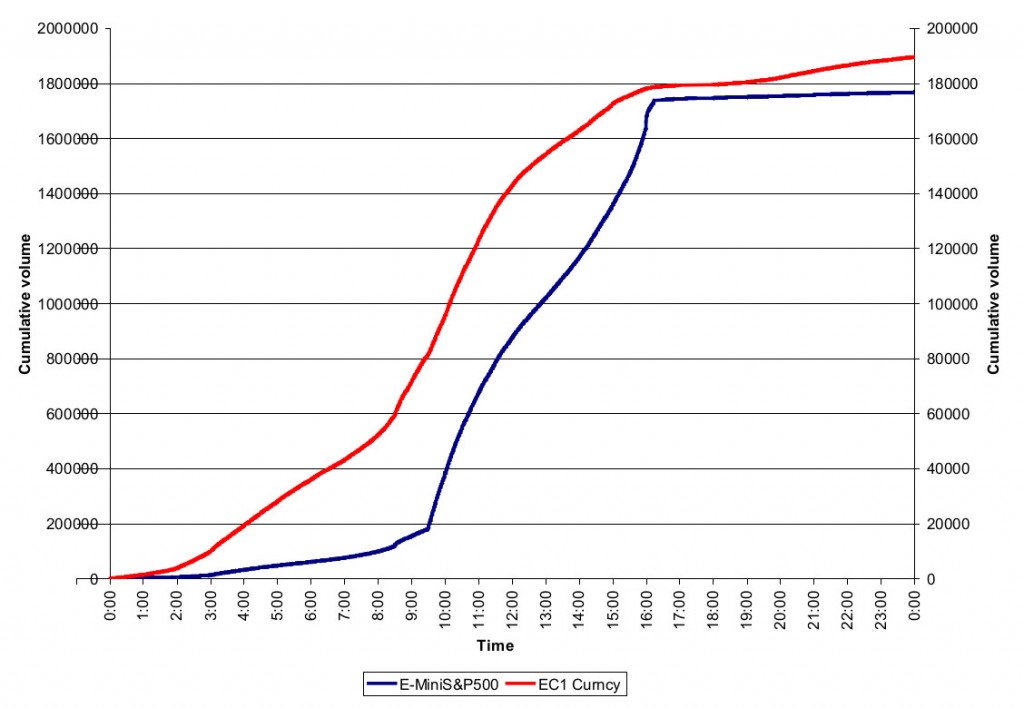
Для проверки робастности нашего вычисления VPIN мы продемонтрируем применение этой метрики для двух наиболее активно торгуемых фьючерсных контрактов: E-mini S&P500 (торгуемый на СМЕ) и фьючерс на сырую нефть WTI (торгуемый на NYMEX). Выборка взята на интервале с 1 января 2008 года по 6 июня 2011 года, сшитая по точкам наибольшего объема в дни экспираций. Размер пакета возьмем равным 1/50 от среднего дневного объема нашей выборки (V). Параметры вычисляются в скользящем окне размером n=50 ( что эквивалентно одному среднему дню по объему).
S&P500
На графике в заглавии поста показан ценовой график фьючерса E-mini S&P500 и его метрики VPIN. Метрика токсичности в основном стабильна, хотя и демонстрирует значительную волатильность. Отметим, что VPIN достигает наивысшего уровня в выборке 6 мая 2010 года, когда на бирже произошел большой обвал котировок. Такой высокий уровень VPIN согласован с потоком ордеров, который был большей частью односторонним в это время. Такая исключительная токсичность приводит к тому, что некоторые маркет мейкеры вынуждены потреблять ликвидность, вместо того, чтобы предоставлять ее и в итоге прекращают свои операции на рынке.
( Читать дальше )
Блог им. uralpro |Измерение токсичности потока ордеров. VPIN для HFT. Часть 2
- 08 июля 2015, 11:28
- |
Прошлая часть — в моем блоге.
Стандартный подход к вычислению PIN состоит в нахождении методом максимального правдоподобия ненаблюдаемых параметров (α,δ,μ,ϵ) описывающих стохастический процесс трейдов, и последующем вычислением PIN из этих параметров. Мы представим аналитическую оценку токсичности, не требующую промежуточного вычисления ненаблюдаемых величин. Мы обновляем нашу метрику в привязке к объемам для учета скорости прибытия новой информации на рынок. Эта метрика, которая называется VPIN, предоставляет простую оценку токсичности потока ордеров в высокочастотном окружении.
Природа информации и времени
Информация в модели последовательной торговли в общем виде представляет из себя данные, которые несут сообщение о будущем уровне цены актива. На эффективном рынке, значение цены актива отражает его полную информационную величину, в связи с тем, что информированный трейдер стремится получить прибыль от владения этой информацией. Так как маркет-мейкер может занимать как длинную, так и короткую позиции, будущие движения актива влияют на его прибыльность, и он пытается извлечь информацию из паттернов торговли. Эти его попытки отражаются в устанавливаемых уровнях бида и аска.
( Читать дальше )
Блог им. uralpro |Измерение токсичности потока ордеров. VPIN для HFT. Часть 1
- 07 июля 2015, 14:20
- |
В статьях об индикаторе PIN мы определили, что на рынке присутствуют два типа трейдеров — информированные и неинформированные. Заявки неинформированных трейдеров всегда подвержены adverse selection risk со стороны информированных. Ситуация, когда после исполнения таких заявок цена движется в невыгодную для неинформированных участников сторону, называется токсичностью потока ордеров. Индикатор PIN служил для измерения этой токсичности, в данной статье мы рассмотрим усовершенствованный индикатор VPIN, который применим и для высокочастотной торговли. Цикл статей основан на публикации Maureen O’Hara "Flow Toxicity and Liquidity in a High Frequency World". Будет все описываться очень подробно, потому что, кроме нахождения непосредственно VPIN, в этой публикации много интересных выводов и фактов.
( Читать дальше )
Блог им. uralpro |Модель скрытых состояний Маркова. Часть 4
- 20 мая 2015, 14:06
- |
Окончание цикла статей. Начало и другие алгоритмы биржевой торговли смотрите в моем блоге и на сайте.
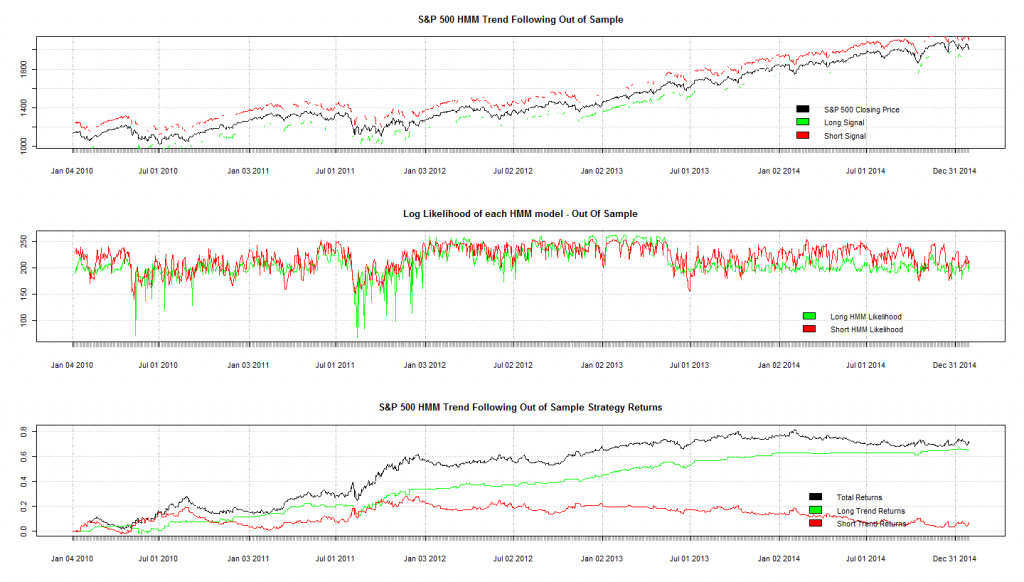
В прошлой части мы продемонстрировали обучение модели Маркова на данных, полученных с помощью симуляции. В данной статье рассмотрим производительность модели на реальных данных. Будем тестировать трендследящую стратегию на индексе S&P500.
В большинстве задач с использованием машинного обучения требуются обучающие данные с разметкой классов (состояний). В нашем случае такой разметки нет, поэтому сначала сгенерируем классы для обучающей выборки.
Мы хотим создать трендследящую стратегию, поэтому должны выбрать участки на выборке цен S&P500, которые соответствуют восходящему и нисходящему трендам ( также можно отметить участки, где тренды отсутствуют). Можно это сделать вручную, а можно применить программу, которая автоматически расставит метки в соответствии с вашими определениями тренда.
( Читать дальше )
Блог им. uralpro |Модель скрытых состояний Маркова. Часть 3
- 18 мая 2015, 14:01
- |
В этой части рассмотрим обучение модели скрытых состояний Маркова на языке R. В прошлых статьях мы изучили математическую основу модели, которая воплощена в библиотеке RHmm. Есть два способа распознавания режимов с помощью модели Маркова, первый — использование одной модели, каждое состояние которой отражает режим, в каком находится рынок. Второй способ подразумевает построение нескольких моделей, каждая из которых создана для одного режима, задача состоит в том, чтобы выбрать ту модель, которая генерирует данные, наиболее соответствующие текущему состоянию рынка. Рассмотрим оба эти способа.
Метод первый — одна модель с несколькими состояниями.
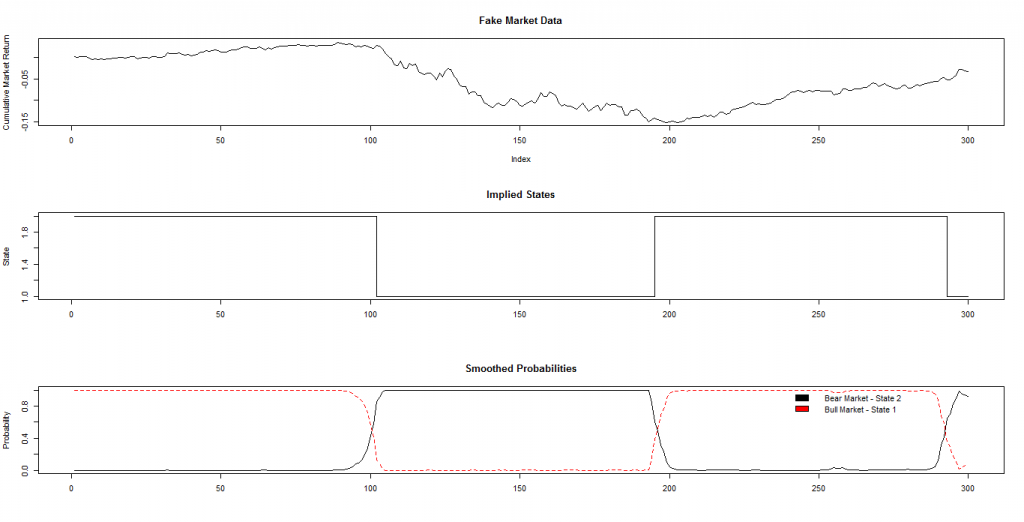
Для обучения модели будем использовать исходные данные, полученные симуляцией из нормального статистического распределения N(mu,sigma), где mu — медиана, sigma — среднеквадратичное отклонение. Распознавание будем производить для двух режимов — бычьего (bull) рынка, на котором наблюдается восходящий тренд и медвежьего (bear) рынка, на котором тренд нисходящий. Соответственно, сгенерируем приращение значений из двух нормальных распределений - N (mu.Bull,sigma.Bull) и N(mu.Bear,sigma.Bear). На рисунке показан результат такой генерации на 300 наблюдений, 100 первых из которых получены из бычьего распределения, 100 вторых — из медвежьего и 100 последних — из бычьего с другими параметрами mu и sigma (каждое приращение будем считать дневным):
( Читать дальше )
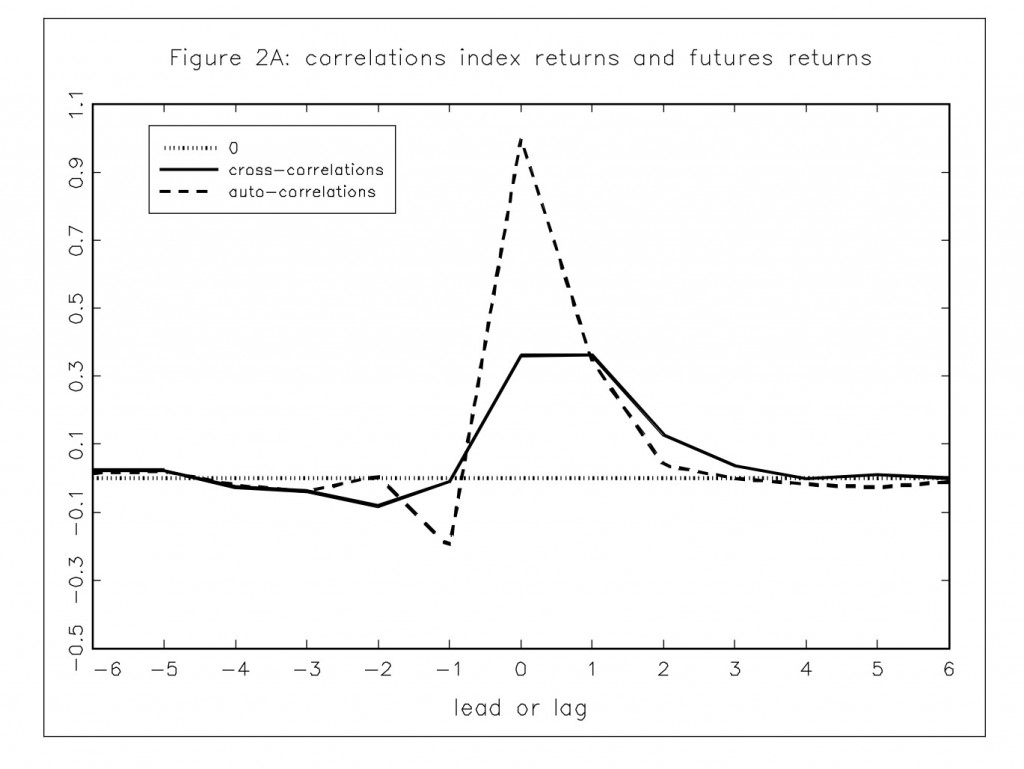
Блог им. uralpro |Модернизация стратегии robot_uralpro. Lead-lag relationship
- 16 апреля 2015, 10:22
- |
Трейдеры, которые приобрели мою программу robot_uralpro (см. пост на смарт-лабе), спрашивают, можно ли доработать алгоритм для применения его на современном рынке? Напомню, стратегия робота основана на взаимоотношении цен синтетического индекса, составляемого динамически из рыночных цен акций, входящих в индекс РТС, и фьючерса RI. Идея «одноногого» статистического арбитража, реализованного в роботе, будет работать и сейчас, только в том случае, если научиться правильно определять, какой актив опережает другой в смысле динамики их цен. Эта статья посвящена правильному выявлению такого взаимодействия, которое в англоязычных источниках называется «lead-lag relationship» -опережение-отставание между разными активами.
Те алготрейдеры, кто не приобретал robot_uralpro, тоже сочтут эту статью полезной, так как lead-lag relationship может использоваться в стратегиях парного трейдинга и им подобным. Например, определив такое взаимодействие, можно исключить из парного трейдинга один из активов ( с учетом того, конечно, что отношение торгуемых инструментов было описано четкой моделью) и значительно увеличить тем самым прибыльность стратегии.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс