Может кому-то будет полезной информация о найденных мной различиях в торговых системах Quik у этих трех брокеров

1. Открытие




( Читать дальше )

1. В папке с Квиком создаем директорию LuaIndicators.
2. В этой папке создаем файл gazp_usd.lua, туда записываем:

Settings = 
{
   Name = "GAZPROM_USD",
   tag = "GAZP",
   tag1 = "GAZP_USDRUB",
   line=
   {
      {Name = "line1", Color = RGB(0, 0, 255), Type = 1,Width = 1}
   }
}

vPrice=1;

function Init()
   return 1
end

function OnCalculate(index)
	local vOutFlag=0;
	local vGazp =(getCandlesByIndex(Settings.tag, 0, index-1, 1)[0].close or 1) ;
	local vUSDRUB=(getCandlesByIndex(Settings.tag1, 0, index-1, 1)[0].close or 1);
	if vGazp>0 then
		vOutFlag=1;
	else
		vOutFlag=0;
	end;
	if vUSDRUB>0 then
		vOutFlag=1;
	else
		vOutFlag=0;
	end;
	if vOutFlag > 0 then
		local Out = vGazp/vUSDRUB;
		vPrice=Out;
	end;
	return  vPrice
end

3. В Квике создаем график с курсом доллара (USDRUB_TOM).
4. К графику добавляем график Газпрома (ГАЗПРОМ ао).
5. Идем в настройки графика, в разделе «Дополнительно» указываем «Идентификатор»: GAZP -для графика с ценой Газпрома, GAZP_USDRUB -для графика с курсом.
6. Добавляем индикатор (выбираем из выпадающего списка GAZPROM_USD).

7. Уменьшаем ненужные поля. Если график не отобразился — даблкликаем на графике — жмем «Применить»:

( Читать дальше )

Добрый день, уважаемые алготрейдеры!
Написал на днях некий алгоритм самостоятельного расчета греков опционов на Qlua срочном рынке ММВБ-РТС, которые 
показываются в виде таблицы значений в Quik.

Подскажите, каким образом добавить в этот алгоритм выставление заявок после сравнения расчетных величин с теми, что транслирует биржа?

( Читать дальше )

Господин AlexChi в своем посте Оптимальное количество бумаг в портфеле выложил такую табличку доходностей портфелей акций в зависимости от их количества.



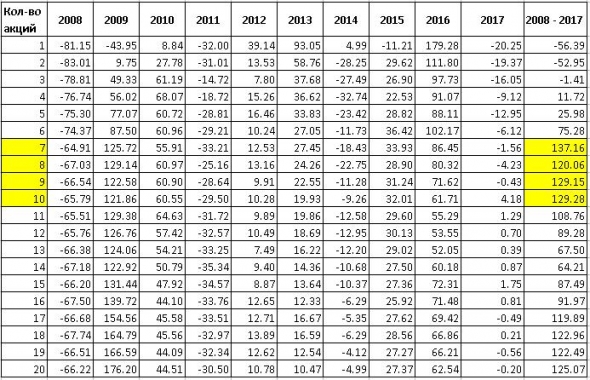
Откинем ошибочную базу рассуждений и посмотрим на сами результаты. Индекс ММВБ за указанный промежуток вырос в номинале всего на 23%. Указанные портфели в разы больше. Классно же!

НО! Даже если откинуть ошибочную статистику, посмотрите на 2014 год. Индекс ММВБ упал за год всего на 8%. А портфели, состоящие из 2-15 акций теряли, порой, в 2-3 раза больше. А если бы индекс упал не на 8%, а на 15%?

Риск всегда обоюден. Кажется, в лучшие годы вы на нем выезжаете, но в худшие годы вас непременно качнет обратно с не меньшей силой. И если риск индекса хоть как-то можно спрогнозировать, то риск одиночных акций — нет и никогда.

З. Ы. Обратите внимание на разброс конечных результатов портфелей из 2-15 акций. От -52% до 137%. То есть, прогнозу не только риск, но и прибыль как элемент риска не поддается.

Оптимальное количество бумаг в портфеле

         
          Очень часто, когда заходит речь о диверсификации, на лице слушателя появляется скептическая улыбка. Казалось бы, что тут можно придумать нового: все уже давным-давно известно, писано и переписано тысячами трейдеров. Если вкратце резюмировать суть большинства рассуждений на тему диверсификации, то можно выделить две основные идеи:

1. Диверсификация необходима.
2. Избыточная диверсификация неэффективна, ибо не позволяет много заработать.

         Не знаю как вас, а меня всегда интересовал вопрос: каким же должно быть оптимальное количество различных бумаг в портфеле? Интуитивно кажется понятным, что если все деньги поставить на одну бумагу, то риск будет очень велик, и подобная торговля уже сильно смахивает на лотерею (угадал/не угадал). С другой стороны, если купить акции около 100 различных компаний, то, помимо проблем с управлением и анализом такого большого портфеля, рассчитывать на приличную доходность тоже можно с большой натяжкой. Как же быть? Сколько бумаг покупать? Прежде чем дать свой ответ на этот вопрос, мне кажется необходимым сделать небольшую оговорку: я вполне отдаю себе отчет, что каждый раз бывает по-разному, иногда портфель, сформированный из всего 2 бумаг, обгонит портфель из 10 бумаг, а когда-то будет наоборот. Тем не менее, мне хотелось бы провести исследование на статистических данных для ответа на вопрос, какое же число бумаг будет оптимальным наиболее часто или даже точнее будет сказать так: какой интервал бумаг (от и до, например от 6 до 10, или от 10 до 15 и т.д.) обеспечит наибольшую доходность.

( Читать дальше )

    Может кому будет интересен скрипт на QLUA, который выступает простым бенчмарком ОФЗ с постоянным купоном к ставке ЦБ.
Основные параметры доходность и премия к ставке ЦБ, с учетом дюрации.
Скрипт не работает онлайн (оперативность тут не принципиальна), при запуске собирает параметры в таблицу и выводит на экран.
В дальнейшем планируется эти данные использовать для анализа премии доходности по дюрации для муниципальных и корпоративных облигаций к ОФЗ.




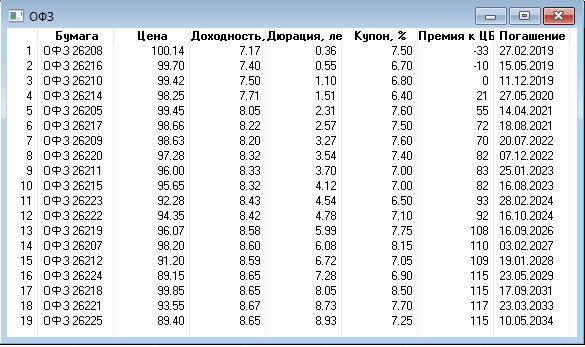
    Код скрипта на github (на github две версии одна в utf-8 для просмотра и основная версия в win1251, т.к. quik понимает только его):
github.com/trantor77/lua_scripts/boundsOFZ.lua

    Код скрипта:

--переменные
keyRateCB = 7.5
classCode = "TQOB"

function CreateTable()
    t_id = AllocTable()
    AddColumn(t_id, 0, "Бумага", true, QTABLE_STRING_TYPE, 15)
    AddColumn(t_id, 1, "Цена", true, QTABLE_DOUBLE_TYPE, 15)
    AddColumn(t_id, 2, "Доходность, %", true, QTABLE_DOUBLE_TYPE, 15)
    AddColumn(t_id, 3, "Дюрация, лет", true, QTABLE_DOUBLE_TYPE, 15)
    AddColumn(t_id, 4, "Купон, %", true, QTABLE_DOUBLE_TYPE, 15)
    AddColumn(t_id, 5, "Премия к ЦБ, бп", true, QTABLE_INT_TYPE, 15)
    AddColumn(t_id, 6, "Погашение", true, QTABLE_STRING_TYPE, 15)
    t = CreateWindow(t_id)
    SetWindowCaption(t_id, "ОФЗ")
end

function string.split(str, sep)
    local fields = {}
    str:gsub(string.format("([^%s]+)", sep), function(f_c) fields[#fields + 1] = f_c end)
    return fields
end

function getParamNumber(code, param)
    return tonumber(getParamEx(classCode, code, param).param_value)
end

function formatData(prm)
    return string.format("%02d.%02d.%04d", prm%100, (prm%10000)/100, prm/10000)
end

CreateTable()

arr = {}
sec_list = getClassSecurities(classCode)
sec_listTable = string.split(sec_list, ',')
j = 0
for i = 1, #sec_listTable do
    secCode = sec_listTable[i]
    securityInfo = getSecurityInfo(classCode, secCode)
    short_name = securityInfo.short_name
    if short_name:find("ОФЗ 26") ~= nil then
        j = j + 1
        r = {}
        r["short_name"] = short_name
        r["price"] = getParamNumber(securityInfo.code, "PREVPRICE")
        r["yield"] = getParamNumber(securityInfo.code, "YIELD")
        r["duration"] = getParamNumber(securityInfo.code, "DURATION")/365
        couponvalue = getParamNumber(securityInfo.code, "COUPONVALUE")
        couponperiod = getParamNumber(securityInfo.code, "COUPONPERIOD")
        r["coupon"] = ((365/couponperiod) * couponvalue)/10
        r["bonus"] = (r["yield"] - keyRateCB)*100
        r["mat_date"] = getParamNumber(securityInfo.code, "MAT_DATE")
        table.insert(arr, j, r)
    end
end

table.sort(arr, function(a,b) return a["duration"] < b["duration"] end)

for j = 1, #arr do
    row = InsertRow(t_id, -1)
    SetCell(t_id, row, 0, arr[j]["short_name"])
    price = arr[j]["price"]
    SetCell(t_id, row, 1, string.format("%.2f", price), price)
    yield = arr[j]["yield"]
    SetCell(t_id, row, 2, string.format("%.2f", yield), yield)
    duration = arr[j]["duration"]
    SetCell(t_id, row, 3, string.format("%.2f", duration), duration)
    coupon = arr[j]["coupon"]
    SetCell(t_id, row, 4, string.format("%.2f", coupon), coupon)
    bonus = arr[j]["bonus"]
    SetCell(t_id, row, 5, string.format("%.0f", bonus), bonus)
    mat_date = arr[j]["mat_date"]
    SetCell(t_id, row, 6, formatData(mat_date), mat_date)
end

Всем здравствовать! Давно не писал заметок.
Мой путь в алготорговле на данный момент оказывается следующим:
1. Создание оболочек (расчета и хранения стат. данных и индикаторов, сама МТС (конструктор стратегий), визуализация), т.к. все самописно на базах access. В планах модуль управления капиталом, но до этого дойдет только в случае выхода в «стабильный» плюс.
Вы даже не представляете сколько нюансов при написании всего с нуля самостоятельно возникало.
Но было интересно. В настоящее время все функционирует стабильно: бот не теряет позиций,  проблема кросс-сделок решена, реальная и виртуальная (тестовая) торговля есть, каждая позиция автономна: входы и выходы (тэйк-профит, стоп-лосс, трэйл стол-лосс) по 1 лоту.
В общем механика работает. Дело за логикой.
2. Правильные входы. Тут долгая дорога, у каждого своя. Сейчас торгуется «контртренд» интрадэй, без переноса позиций. 5 возможных входов. Сейчас входы в целом устраивают, лучше — те, которые с оглядкой на объем. 
3. Правильные выходы. Здесь тоже не все просто. Смысл в том, что все и так знают, — как на практике найти оптимальную точку выхода? В общем сейчас 7 возможных сигналов на выход. На практике я пробовал почти все, и при сильно коротких лоссах и трэйлах — сразу падал результат. Т.к. 20-30% правильных сделок  давали 80% ПНЛ. 

( Читать дальше )

Продолжение, начало: Торговая стратегия ч. 1

В общем случае необходимо признать, что точно прогнозировать движение цен невозможно. Котировки зависят от сделок множества участников рынка и предсказать конкретное движение в данный момент можно только случайно. Аналогично, не представляется возможным точно определить момент разворота тренда в том или ином инструменте, хотя по объёму торгов и некоторым фигурам теханализа можно сделать вывод, например, об окончании сильного медвежьего или бычьего тренда.

Взяв эти умозаключения за принципы работы на рынке, я решил начинать открытие длинных позиций с малой лотажности. Логика действия следующая: покупаем 100 акций выбранной компании и смотрим на динамику цены. Если цена идёт в нашу сторону, то в соответствии с первым правилом лонговая позиция вверх никогда не усредняется, а подыскивается другой инструмент для набора позиции. Говоря проще, «пирамидинг» по ап-тренду полностью исключён. Если цена идёт против нас, то продолжается набор позиции, средняя начинает движение вниз вслед за «медвежьим» трендом. Наиболее комфортны низкие цены, в диапазоне $5-$20 за акцию. Здесь с психологической точки зрения важно соотношение прибыль/убыток: маловероятно, что крупная компания будет торговаться около 0, и даже если цена уйдёт значительно ниже, изначальная ставка была небольшой и мы теряем немного. Если же случится разворот, то возможны два варианта: либо мы заработаем немного, не успев набрать достаточную позу, либо в процессе усреднения наберём достаточный объём к моменту, когда в инструменте начнётся бычий тренд и наша прибыль будет значительной. Этот метод называется

( Читать дальше )

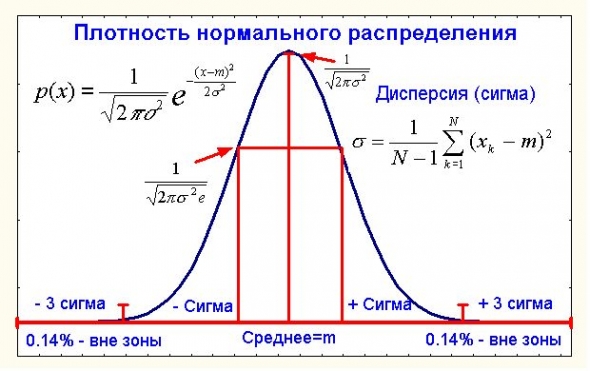
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

 
 

А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x

( Читать дальше )

Давно известно, что если вы хотите купить какую-то акцию дешевле — продайте на нее пут не в деньгах. Например хотите сбер по 180? Продайте 180й пут. Если цена упадет ниже 180 — то вы получите акцию по 180 и еще премию по путу. (например 2) и таким образом эффективная цена покупки будет 178. Ну, а если цена не упала — то получите просто истекшую премию в размере 2, что в пересчете на ГО довольно неплохая доходность. Пример выше — условный, надо смотреть на цены, страйки, волатильность. Но есть одно простое правило — путы лучше продавать тогда, когда рынок уже припал и вола подскочила и часть падения уже пройдена. (Так, сейчас кто-то бросится писать коммент про мой 2008й год. Да, такое бывает. Но сейчас этих предпосылок, вроде как, нет).
Чем еще хорошо продавать путы? что если акция болтается в диапазоне, то вы собираете премию. Обычный владелец стока при неизменной (почти) цене акции получит лишь дивиденды, а вы — опционную премию. (правда не будет дивидендов)

Но тут возникает два момента — первый, с опционами не все знакомы и не все связываются и второй — не на каждый инструмент есть опцион. Поэтому сейчас я расскажу стратегию торговли, для которой не нужны опционы, но суть ее особо не поменяется. Более того, добавятся дивиденды.

( Читать дальше )