Избранное трейдера Denis Lisin
Книга для тех, кто хочет систематизировать свою торговлю или создавать торговых роботов
- 09 апреля 2019, 20:15
- |
Автор — известный в трейдерской среде mehanizator. Создатель сайта для алгоритмических трейдеров long-short.pro
Книга является квинтэссенцией многолетнего опыта автора в области исследований свойств рынка и разработки механических торговых систем.
Являясь практическим руководством к действию, книга глава за главой проводит читателя в мир систематизированной торговли, правил, алгоритма принятия решений и проверки тех или иных гипотез.
Состоит из 4 последовательно связанных глав. Внимание следует уделить всем главам, даже несмотря на то, что кажется что в начале книги автор льет воду. На самом деле воды в книги нет, описательные разделы поведения рыночных участников и свойств рынка необходимы в начале книги, чтобы в последующем читатель смог формировать рабочие гипотезы и, проверив их затем на тестах, выйти на устойчивую алгоримическую (системную) торговлю.
Рекомендую к прочтению всем, кто хочет отойти от импровизации и перейти на системный трейдинг — позволит сэкономить кучу времени и избежать иллюзий простоты этого вида деятельности.
- комментировать
- ★15
- Комментарии ( 2 )
TSLab Мартингейл
- 09 апреля 2019, 09:10
- |
Давайте отдельно и четко формулировать атомарную информацию, которую можно использовать для разных нужд.
Пример реализации на кубиках TSLab (без кода) простейшего, (всегда сливающего, до добра не доводящего, и рано или поздно накажущего) но всеми очень любимого Мартингейла для ФОРТС.
Просто пример, для вопроса очередного граалеищщущего новичка «с чего начать».
Скрипт (внезапно) даже зарабатывает. Ну, если параметры подогнать, разумеется.
Выглядит следующим образом:

Для упрощения схемы (это всё же просто пример) для закрытия сделки я применил не отдельные Тейк и Стоп, а кубик «Трейлинг Стоп Абс», при этом выставил в нем Stop Loss = Trail Enable, а Trail Loss = 0, для того, чтобы (теоретически) закрывались сразу при касании тейка. Можете поменять параметры и попробовать еще и трейлить.
( Читать дальше )
Доработал zigzag5
- 08 апреля 2019, 23:49
- |
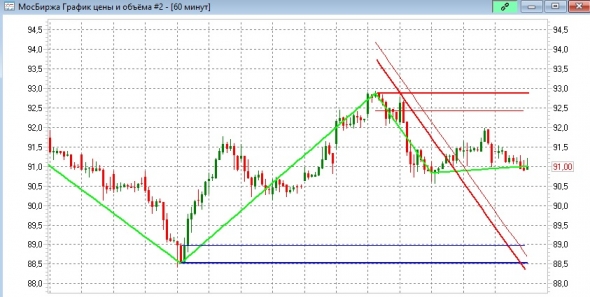
код индикатора:
Settings=
{
Name = "Zigzag5", -- название индикатора
delta=2, -- параметр индикатора
deltaY=1, -- параметр индикатора
linedeltaY=0.75, -- параметр индикатора
line=
{
{
Name = "zigzagline3",
Type =TYPE_LINE,
Width = 2,
Color = RGB(0,255, 0)
},
{
Name = "upline",
Type =TYPE_LINE,
Width = 2,
Color = RGB(255,0, 0)
},
{
Name = "lowline",
Type =TYPE_LINE,
Width = 2,
Color = RGB(0,0, 255)
},
{
Name = "declineline",
Type =TYPE_LINE,
Width = 2,
Color = RGB(255,0, 0)
},
{
Name = "upline2",
Type =TYPE_LINE,
Width = 1,
Color = RGB(255,0, 0)
},
{
Name = "lowline2",
Type =TYPE_LINE,
Width = 1,
Color = RGB(0,0, 255)
},
{
Name = "declineline2",
Type =TYPE_LINE,
Width = 1,
Color = RGB(255,0, 0)
}
}
}
function getradius(x, y)
return math.sqrt(Settings.deltaY*y*y+x*x)
end
function koef(val)
return 1 - 1/(1-1/val)
end
function Init()
vMin = 0
vMax = 0
vMinindex = 0
vMaxindex = 0
voldMinindex = 0
voldMaxindex = 0
upval = 0
lowval = 0
upindex = 1
lowindex = 1
veu = nil
vel = nil
curfrom = 1
curto = 1
return 7
end
function OnCalculate(index)
local printz = 0
vsize = Size()
ve = nil
veu = nil
vel = nil
curv = nil
veu2 = nil
vel2 = nil
curv2 = nil
if index == 1 then
vMin = C(index)
vMax = C(index)
vMinindex = index
vMaxindex = index
voldMinindex = index
voldMaxindex = index
ve = C(index)
else
if voldMaxindex >= voldMinindex then
if C(index) > (1 + Settings.delta/100)*vMin then
vMin = C(index)
vMax = C(index)
vMaxindex = index
voldMinindex = vMinindex
vFrom = voldMaxindex
vTo = vMinindex
printz = 1
if (C(vMinindex) > C(vsize)) and (upval > koef(getradius(vsize - vMinindex, C(vMinindex) - C(vsize)))) then
upval = koef(getradius(vsize - vMinindex, C(vMinindex) - C(vsize)))
upindex = vMinindex
end
if (C(vMinindex) < C(vsize)) and (lowval > koef(getradius(vsize - vMinindex, C(vMinindex) - C(vsize)))) then
lowval = koef(getradius(vsize - vMinindex, C(vMinindex) - C(vsize)))
lowindex = vMinindex
end
curfrom = voldMaxindex
curto = voldMinindex
else
if vMin > C(index) then
vMin = C(index)
vMinindex = index
vFrom = voldMaxindex
vTo = index
printz = 0
curto = index
else
vFrom = vMinindex
vTo = index
printz = 0
end
curfrom = voldMaxindex
end
else
if voldMaxindex <= voldMinindex then
if C(index) < (1 - Settings.delta/100)*vMax then
vMax = C(index)
vMin = C(index)
vMinindex = index
voldMaxindex = vMaxindex
vFrom = voldMinindex
vTo = vMaxindex
printz = 1
if (C(vMaxindex) > C(vsize)) and (upval > koef(getradius(vsize - vMaxindex, C(vMaxindex) - C(vsize)))) then
upval = koef(getradius(vsize - vMaxindex, C(vMaxindex) - C(vsize)))
upindex = vMaxindex
end
if (C(vMaxindex) < C(vsize)) and (lowval > koef(getradius(vsize - vMaxindex, C(vMaxindex) - C(vsize)))) then
lowval = koef(getradius(vsize - vMaxindex, C(vMaxindex) - C(vsize)))
lowindex = vMaxindex
end
curfrom = voldMinindex
curto = voldMaxindex
else
if vMax < C(index) then
vMax = C(index)
vMaxindex = index
vFrom = voldMinindex
vTo = index
printz = 0
curto = index
else
vFrom = vMaxindex
vTo = index
printz = 0
end
curfrom = voldMinindex
end
end
end
if (printz == 1) or (Size() == index) then
for i = vFrom, vTo do
k = (C(vTo)- C(vFrom))/(vTo- vFrom)
v = i*k + C(vTo) - vTo*k
SetValue(i, 1, v)
ve = v
end
if (Size() == index) then
ve = C(index)
if voldMaxindex >= voldMinindex then
vFrom = voldMaxindex
vTo = vMinindex
end
if voldMaxindex <= voldMinindex then
vFrom = voldMinindex
vTo = vMaxindex
end
for i = vFrom, vTo do
k = (C(vTo)- C(vFrom))/(vTo- vFrom)
v = i*k + C(vTo) - vTo*k
SetValue(i, 1, v)
end
-- up level line
if upindex ~= nil then
if C(upindex) > C(index) then
for i = upindex, index do
SetValue(i, 2, C(upindex))
SetValue(i, 5, C(upindex)-Settings.linedeltaY*C(vsize)/100)
end
veu = C(upindex)
end
end
-- low level line
if lowindex ~= nil then
if C(lowindex) < C(index) then
for i = lowindex, index do
SetValue(i, 3, C(lowindex))
SetValue(i, 6, C(lowindex)+Settings.linedeltaY*C(vsize)/100)
end
vel = C(lowindex)
end
end
if voldMaxindex >= voldMinindex then
vsign = -1
if curfrom == voldMinindex then
vsign = -1
end
if curfrom == voldMaxindex then
vsign = 1
end
-- inclined line
if curto- curfrom > 0 then
maxcurv = 0
k = (C(curto)- C(curfrom))/(curto- curfrom)
for i = curfrom, curto do
curv = i*k + C(curto) - curto*k
if vsign == -1 then
if L(i) < curv then
if maxcurv < curv - L(i) then
maxcurv = curv - L(i)
end
end
else
if H(i) > curv then
if maxcurv < H(i) - curv then
maxcurv = H(i) - curv
end
end
end
end
for i = curfrom, index do
curv = i*k + C(curto) - curto*k + vsign*maxcurv
SetValue(i, 4,curv)
curv2 = curv+ vsign*Settings.linedeltaY*C(vsize)/100
SetValue(i, 7,curv2)
end
end
curv = nil
end
if voldMaxindex <= voldMinindex then
vsign = -1
if curfrom == voldMaxindex then
vsign = 1
end
if curfrom == voldMinindex then
vsign = -1
end
-- inclined line
if curto- curfrom > 0 then
maxcurv = 0
k = (C(curto)- C(curfrom))/(curto- curfrom)
for i = curfrom, curto do
curv = i*k + C(curto) - curto*k
if vsign == -1 then
if L(i) < curv then
if maxcurv < curv - L(i) then
maxcurv = curv - L(i)
end
end
else
if H(i) > curv then
if maxcurv < H(i) - curv then
maxcurv = H(i) - curv
end
end
end
end
for i = curfrom, index do
k = (C(curto)- C(curfrom))/(curto- curfrom)
curv = i*k + C(curto) - curto*k + vsign*maxcurv
SetValue(i, 4,curv)
curv2 = curv+ vsign*Settings.linedeltaY*C(vsize)/100
SetValue(i, 7,curv2)
end
end
curv = nil
end
end
end
end
return ve, veu, vel, curv, veu2, vel2, curv2
endТабличка NineNot для трейдера
- 08 апреля 2019, 18:53
- |
Введение
В воскресенье 7 апреля я перебирал полки в шкафах, просматривая старые бумаги и выбрасывая те, которые уже не пригодятся. За долгое время накопилось много бесполезного хлама, который надо было выбросить. Какие-то старые чеки, квитанции, ненужные распечатки. Так я перебирал бумаги одну за другой, сортируя, что пойдет на выброс, а что еще может когда-то пригодиться, и вдруг на пол упала до боли знакомая старая затертая картонка. Боже мой! Как давно это было! Вроде бы не так уж давно, но на самом деле целую трейдерскую жизнь назад! Воспоминания нахлынули на меня…
Затертая замусоленная старая табличка, обычный кусок картонки и неаккуратно приклеенная скотчем распечатка. Но сколько денег она мне помогла заработать, а сколько денег благодаря ей я не потерял!

Табличка NineNot (9 “не”).
( Читать дальше )
Основы (дифуры Ито)
- 08 апреля 2019, 10:42
- |
Был такой дядька. Киёси Ито. Работал в статистическом управлении и писал книжки. Интернета тогда не было, поэтому он, как и Тимофей Мартынов, делал книжки из бумаги и писал в них ручками. Писал он о теории вероятности и стохастике, то есть про кроликов, и внимание. За эти работы он получил степень доктора философии. То есть, тут не столько вопрос в математике, сколько в философии.
Дифур это такой способ записи философской мысли. Когда вы рисуете каналы по лоу на графике, вы даже не задумываетесь, что это касательная, а значит производная функции цены от времени. Для записи мысли или идеи мы воспользуемся дифурами, а потом переведем их. В общем, их особо ни кто не решает. Берут справочник производных и вуаля. dx/dt = α x => x(t) = x0 e^αt. Уравнение разряда конденсатора dx/dt. У каждого уважающего опционщика такой справочник есть. Это греки опционов. Там дифур и его значение в обычной формуле, куда можно уже цифры подставить. И все.
Из предыдущего материала мы помним. dx = µ x dt + σ x δW. Мгновенное изменение цены=среднему изменению+размеру изменения*случайное изменение. Давайте этим философским языком пообщаемся. И легче всего это понять методом Кирилла Ильинского.
( Читать дальше )
zigzag5 переработал алгоритм горизонтальных уровней
- 06 апреля 2019, 20:19
- |
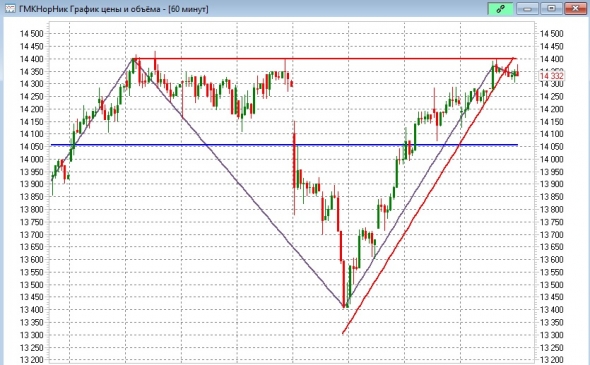
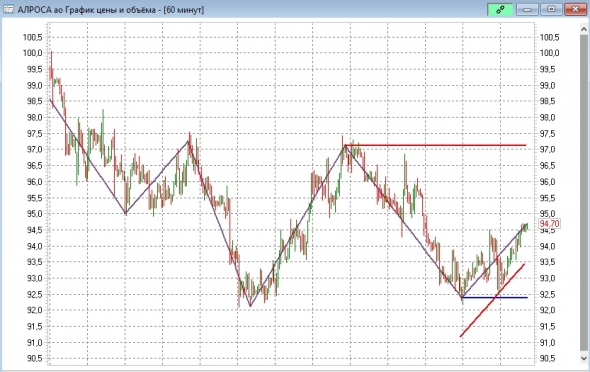
( Читать дальше )
Пэйроллы за 100 лет
- 04 апреля 2019, 22:09
- |
Осваиваю базу данных quandl.com
Оттуда можно качать котировки, а можно и экономическую статистику. Например, там есть нонфарм-пэйроллы с 1921 года.
Как и положено питону, там всё очень просто.
Не знаю почему, пэйроллы с 1947 года по значениям сильно отличаются от предыдущих:

Будем брать те, которые идут с 1947 года.
Инструкция шаг за шагом.
1. Качаем питон, если он у вас до сих пор не установлен: https://www.python.org/
2. Открываем командную строку cmd.exe (чёрное окошко).
3. Пишем в нём pip install quandl

( Читать дальше )
Робот "Два Боллинджера" с исходниками
- 04 апреля 2019, 16:19
- |
Итак, робот на двух графиках Боллинджера.
Общий принцип:
1) На цену накладываются два графика Боллинджера: с периодами 20 и 120 (назовем их local и global).
2) В зависимости от параметра внутри робота, входим либо когда цена входит внутрь local-Боллинджера (ContrTrendFlag=1), либо выходит из него (ContrTrendFlag=0).
3) Дополнительный фильтр: Лонг только когда когда мы в верхней половине global-Боллинджера, шорт — если в нижней.
Данные робот берет из графиков, так что график должен быть открыт, и прописаны идентификаторы.
График с двумя Боллинджерами выглядит примерно так:

Настройки на цене и индикаторах не забудьте:

( Читать дальше )
Как я искусственный интеллект торговать научил
- 01 апреля 2019, 12:44
- |
Однажды великий гуру трейдинга и знаток анекдотов Александр Михайлович (который Герчик) в одном из своих семинаров рассказал про один случай, когда он пытался алгоритмизировать работу с уровнями и нанял целого математика, чтобы тот разработал мат.аппарат и запрограммировал сигналы для отбоя/пробоя. Целый математик бился над задачей как рыба об лед, но, видимо, математик он был так себе и поэтому задачу решить не смог.
Даже я, на тот момент имеющий в активе три класса церковно-приходской, долго недоумевал, как можно было не решить такую простейшую задачу. Это же легче легкого, думал я: хочешь запрограммировать горизонтальные уровни — тупо вбей в систему справочник круглых чисел, хочешь запрограммировать вершину параболы — пиши регрессию. И так далее.
Потом времена ушли далеко вперед и появился Искусственный Интеллект (ИИ), который легко решает эту задачу, даже без понимания, как оно должно работать.
Собственно, ИИ появился еще лет 50 назад. Но в те давние времена (уже почти былинные), когда и трава была зеленее и небо голубее, компьютерное железо было не способно решать задачи такого уровня. Сегодня ситуация изменилась.
( Читать дальше )
Прибыльные паттерны
- 01 апреля 2019, 12:00
- |
Сделал еще один вариант сервиса по поиску похожих паттернов — ТОП текущих прибыльных паттернов.
Работает это примерно так:
1. Берем текущий сформировавшийся паттерн на графике:
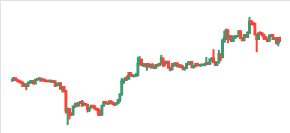
2. Для него ищем 100 наиболее похожих паттерна в прошлом на разных инструментах:
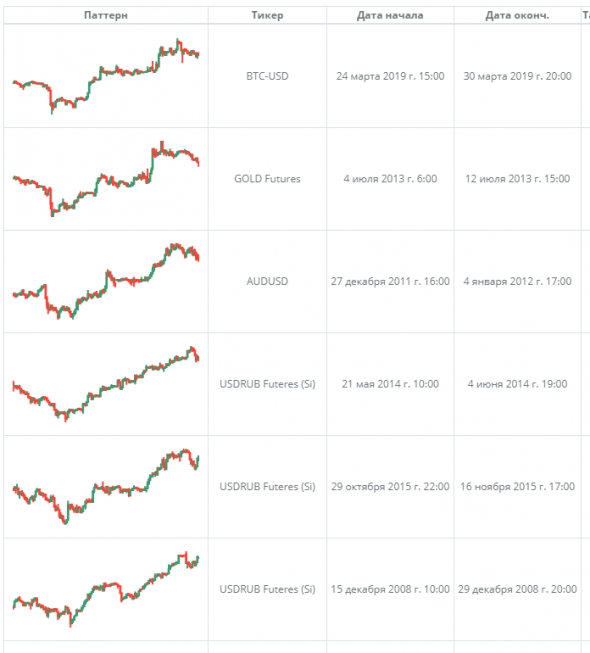
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лидеры роста и падения ммвб
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал
