теория
Фридман vs. Кейнс (Экономические теории)
- 09 декабря 2021, 11:30
- |

Джон Кейнс и Милтон Фридман являются величайшими экономистами, у обоих есть своя теория и своё течение.
Кейнс говорит, нам надо регулировать экономические циклы наращиванием денежной массы и сокращением ключевой ставки, т.к. люди чаще склонны сохранять деньги, а не тратить, а совокупный спрос всегда ниже совокупного предложения, поэтому будем обесценивать их деньги, чтобы они с ними проще и быстрее расставались.
Фридман говорит, что нужно постоянно придерживаться стратегии наращивания денежной массы и отказаться от кредитно-денежной политики вовсе.
А прикол в том, что сторонники Кейнсианства ненавидят сторонников Фридмана и наоборот, считают теории друг друга деструктивными и антагонистичными.
Посему я спрашиваю у тебя, мудрый смартлаб, в чём существенная разница теорий? В обоих случаях наращивание денежной массы, вливание государством в экономику денег для стимуляции.
- комментировать
- ★1
- Комментарии ( 22 )
Теория Грааля
- 23 октября 2021, 19:24
- |
Вот этим умом:

Сегодня торгов нет. Мозг отдыхает. В нем полно глюкозы. Предлагаю загрузить его поиском математического доказательства Теории Грааля, которая звучит так:
Алгоритм, генерирующий стабильную прибыль на известных данных, способен генерировать приемлемую прибыль на неизвестных данных.
Короткая формулировка Теории Грааля (для девушек) звучит так:
Прошлое повторяется в будущем.
Причиной появления этой теории является особенность человеческого восприятия рисунков. Смотрим на часовой график Сбера:

( Читать дальше )
Маржа на американском рынке и риски маржинальной торговли
- 06 сентября 2021, 14:11
- |
Поэтому расскажу немного теории о торговле на американских биржах.
Маржа на американском рынке и риски маржинальной торговли.
Маржа или маржинальные требования – это залог, который брокер резервирует на вашем счете, за открытие позиции.
📋 Например, стоимость одного лота акций Apple равна $15 000. Но вам необязательно иметь $15 000, чтобы купить акцию Apple. Interactive Brokers установил для акций Apple маржинальные требования в размере 25% от стоимости. То есть для покупки 1 лота достаточно иметь $3 750 на счете. Такая покупка актива без полного обеспечения деньгами называется маржинальная торговля.

С одной стороны, маржинальная торговля позволяет получать бОльшую прибыль 📈.
С другой стороны, маржинальная торговля
( Читать дальше )
Почему пузыри не так легко сдуть?
- 02 августа 2021, 13:19
- |

Факторов, которые влияют на возможность сдуть пузырь много: действия монетарных, фискальных и финансовых властей, институциональных и иррациональных инвесторов и т.д. и т.п. Описать все в одном посте не получится. Я хотел бы сконцентрироваться на некоторых аспектах, которые касаются скорее технических возможностей у инвесторов и не пускаться в вопросы политического и макроэкономического характера.
Чтобы объяснить трудности связанные с возможностью сдуть пузырь необходимо немного узнать о такой гипотезе – как ограниченность арбитража, которую в разных вариантах изложили Миллер, Шлейфер, Вишнего. Основа гипотезы тривиальна — на рынке действуют два типа инвесторов: иррациональные (noise или feedback traders) и рациональные (smart money). Иррациональные инвесторы в основном чайники, не разбираются в стоимости активов и в своем подавляющем большинстве смотрят на них как на «бумажки», у которых есть какая-то цена, за которую их покупают и продают. Поэтому для них важнее чтобы цена двигалась (в основном росла) по любым основаниям. Рациональные же инвесторы способны оценить справедливую стоимость, но как оказывается, в случае если цена на актив сильно завышена, они немногое могут сделать. Из идеи арбитражного формирования цены, рациональные инвесторы должны занять короткую позицию, тем самым начав двигать цену к равновесной. Но на рынке возможность шортовых позиций реально ограничена. Есть также ассиметрия в ограниченности. В случае недооценки актива ограниченность тоже присутствует, но как показывают исследования купить акции все-таки проще, чем продать в короткую.
( Читать дальше )
Теория Большего Дурака
- 15 июня 2021, 19:03
- |
Статью о Теории Большего Дурака в вики можете нагуглить сами.
Напишу очень кратко.
Покупая актив мы надеемся, что он будет расти. Как нам, трейдерам, всем известно, чтобы актив рос он должен пользоваться спросом(т.е его должны покупать, даже если эти покупки вызваны срабатыванием стоп-лоссов).Группа трейдеров купившая в самом начале движения (перед заходом в актив основной части трейдеров) начинает фиксировать прибыль(тут в большинстве случаев играет страх потерять прибыль, т.к все прекрасно знают если пожадничать то другие начнут закрывать свои позиции и можно потерять часть прибыли или даже всю). Продают группе отстающих, которые все еще надеются на рост актива. Со временем покупатели заканчиваются и цена разворачивается, трейдеры купившие последние по более высоким ценам оказываются в ловушке. Теперь уже фиксации позиций происходят даже в убыток( опять же играет свою роль страх, что убыток станет еще больше)
Исходя из этого перед трейдером появляется задача научится определять начало движения, чтобы не быть отстающим(кормом на рынке)
Добавим сюда мультифрактальность и медведей, и у нас получится настоящий рынок))
Волновая структура на мелком таймфрейме
- 13 февраля 2021, 16:18
- |
Сегодня хочу показать, насколько хорошо могут отрабатыватьcя базовые принципы волнового анализа даже на мелких таймфреймах.
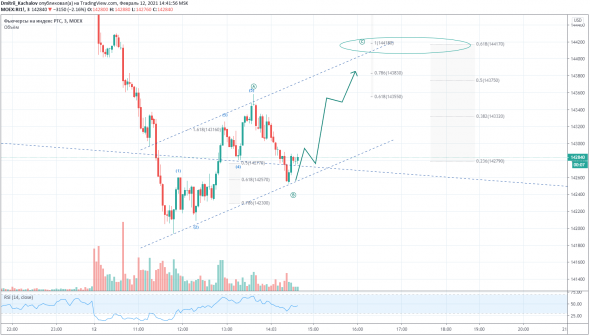
📎 На первой картинке изображен прогноз движения цены от локального минимума вчерашнего дня на трехминутном таймфрейме.
Отчетливо виден пятиволновый импульс на старте. Этот импульс по своей природе может являться либо волной [1] импульса большего порядка, либо волной [A] зигзагообразной коррекции. По графику волна (3)of[A] примерно равна 1,618 волны (1)of[A]. А волна [B] достигает уровня 0,618 от волны [A] прежде чем снова развернуться.
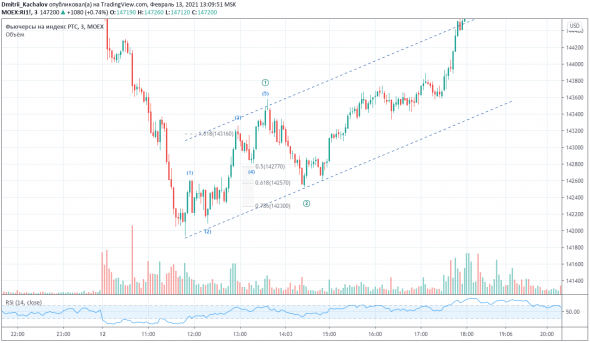
( Читать дальше )
Всегда интересовало - кто такие, эти Арии!
- 10 января 2021, 21:55
- |
Термин «арийский» происходит от протоиндоиранского корня *arya, означавшего этноним, которым индоиранцы называли своих предков ариев. Родственным словом на санскрите является слово ārya (деванагари: आर्य) — по происхождению этническое самоназвание, в классическом санскрите означающее «благородный, почтенный, знатный». От родственного слова в древнеперсидском языке ariya- (древнеперсидская клинопись: 𐎠𐎼𐎡𐎹) происходят современные названия «Иран» и «иранцы».
иран. *aryānām xšaθra- «Царство ариев»… Очень интересно!
Книга не рекомендуется для чтения людям с тонкой душевной организацией!
Вообще интересная книга. Знакомит с гипотезами Германа Вирта и Бала Тилака об «Арктической Родине в Ведах» протоарийцев и разработке возможного протоязыка на основании наблюдения полярного годового цикла.
( Читать дальше )
Ошибки новичка на бирже
- 02 января 2021, 13:02
- |

Первое — это попытка поторговать тогда, когда захотелось этого. Запускается торговая система и пошли сделки. Но т.к. такое желание не так часто происходит, то и сделки совершаются невпопад. Хороших точек для входа не так много, а это значит в рынок придется входить возможно тогда, rulf вас физически за компом не будет. Это означает что в большинстве случаев хорошие сделки — это отложенные сделки. Это даже и луче, т.к. не придется все время сидеть за компом.
Второе — использование в торговле своих ощущений типа: мне кажется, вроде должно быть так, скорее всего это будет так, аналитики говорят, что… Не должно быть никаких эмоций в торговле. Должна быть только идея, которая обеспечивает вероятность забрать прибыль. Она либо сработает либо не сработает, ничего более. Вы всего лишь навсего должны поставить заявку на покупку, если она сработает, то выставить заявку на продажу, и все!
Третье — шортить рынок. Шорт более рискованно предприятие. На рынке нужно максимально снижать риски. Так что шорт — это зло.
Теория позиционного заработка
- 21 ноября 2020, 23:05
- |
2) заранее выставляем заявки чтоб взять эту эффективность максимально широко по рынку
3) за продолжительные заявки никто плату не взимает
4) при большом количестве выставленных заявок, небольшой процент эффективности на рынке даст наполнить и диверсифицировать портфель
5) некоторые акции имеет смысл держать в долгую, чтоб компенсировать недополученную прибыть при длительном росте
6) в долгосрок нужно отправлять те акции, которые более всего мощные по капитализации
подобную технику с весны тестирую на американском рынке, посмотрим, что будет через полгода, средний размер прибыли со сделки примерно 25%
портфель вырос примерно на 50%
в некоторых акциях застрял в некоторых по несколько раз закрывал лонги
процесс происходит волнообразно в соответствии с поведением индекса
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдер
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал

