SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Блог им. gift
Принцип Парето
- 30 января 2012, 15:29
- |
Почему в мире не бывает равенства и почему ничего плохого в этом нет.
Схема эта видна повсюду: 1% богатейших людей контролирует 35% всего мирового богатства. 2% пользователей Twitter отправляют 60% сообщений. В системе здравоохранения наиболее дорогостоящее лечение, необходимое пятой части пациентов, составляет четыре пятых всех расходов. Эти цифры всегда преподносятся как шокирующие, нарушающие нормальный порядок вещей, будто ситуация, в которой деньги или сообщения не распределяются линейно, в наивысшей степени неожиданна. Но ничего неожиданного в этом нет. Вернее, не должно быть.
Итальянский экономист Вильфредо Парето столетие назад выяснил, что в разных странах мира наиболее состоятельные 25% населения контролировали большую часть богатства. Следствия феномена, обнаруженного Парето, известны под множеством имен: правило 80/20, закон Ципфа, распределение по степенному закону, принцип «победитель получает все» — но модель распределения всегда одна: самые богатые, деятельные, имеющие больше всего связей участники системы отвечают за состояния, действия или количество связей, в разы превышающие средние показатели.
Кроме того, данная схема рекурсивна (рекурсия — способ общего определения множества объектов или функций через себя, с использованием ранее заданных частных определений. — Esquire). Это означает, что внутри верхних 20% системы, обнаруживающей распределение Парето, в свою очередь есть свои верхние 20%, которые дают непропорционально больший результат, чем остальные 80%. И так далее. Элемент, который находится на верхушке такой системы, будет обладать гораздо большим весом, чем все остальные (так, в английском языке слово «the» является не только самым распространенным, но и встречается в два раза чаще, чем второе по частоте употребления слово «of»).
Пример распределения Парето
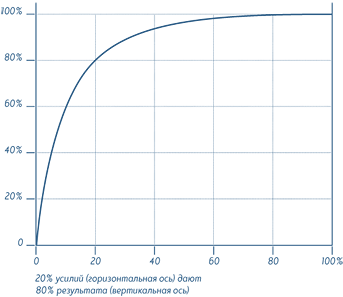
Схема, обнаруженная Парето, оказалась настолько распространенной, что он назвал ее «предсказуемым несоответствием». Впрочем, он был слишком оптимистичен — даже сто лет спустя мы не научились предсказывать это вездесущее несоответствие. Отчасти наше неумение ожидать ожидаемого объясняется тем, что нас учат: хрестоматийное распределение больших систем — это Гауссово распределение, общеизвестное в качестве кривой нормального распределения. Например, на кривой нормального распределения роста среднее значение и медиана (срединная точка в системе) совпадают: средний рост ста американок, отобранных случайным образом, составляет около 165 см, при этом, если всех их выстроить по росту, то высота пятидесятой по счету будет 165 см.
Пример нормального (Гауссова) распределения
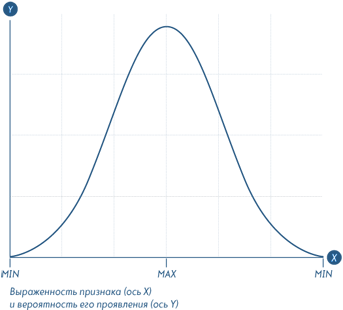
В распределениях Парето все иначе: рекурсивное долевое соотношение 80/20 означает, что среднее находится далеко от середины. Это, в свою очередь, означает, что в подобных системах большинство людей (или того, что подлежит измерению) показывают результат меньше среднего. У экономистов есть шутка: «Когда Билл Гейтс заходит в бар, то все его посетители становятся, в среднем, миллионерами». Распределение Парето проявляется в удивительно большом множестве сложных систем: ему следует частота тэгов к фотографиям на Flickr, сила землетрясений, популярность книг, размер астероидов и количество контактов у ваших друзей. Этот принцип является настолько базовым для научных исследований, что производится даже специально разлинованная бумага, показывающая распределение Парето в виде прямых линий.
Но несмотря на то что науке все это известно уже сто лет, примеры распределений Парето регулярно представляются общественности как аномалии, мешающие ясному видению мира. Мы должны отказаться от мысли, что средний семейный доход и доход средней семьи имеют что-то общее и что самое большое землетрясение или падение на рынке в будущем окажется сопоставимо с самой масштабной катастрофой в прошлом. Чем дольше существует система, тем выше вероятность события, которое в два раза превосходит все предшествующие.
Это не означает, что мы никак не можем воздействовать на такие распределения. Снижение кривой Парето от «головы» к «хвосту» может быть более или менее резким. Иногда политическое или социальное вмешательство способно повлиять на крутизну кривой — налоговая политика может повысить или снизить долю дохода 1% самых богатых жителей страны. Но пока мы не признали, что есть множество систем, в которых действует распределение Парето, и что они останутся таковыми всегда, мы даже не начали их осмысливать. Вероятно, мы просто пытаемся надеть на «корову» Парето «седло» Гаусса. Сто лет спустя после открытия «предсказуемого несоответствия» мы должны довести дело до конца и все-таки начать его предвидеть.
Схема эта видна повсюду: 1% богатейших людей контролирует 35% всего мирового богатства. 2% пользователей Twitter отправляют 60% сообщений. В системе здравоохранения наиболее дорогостоящее лечение, необходимое пятой части пациентов, составляет четыре пятых всех расходов. Эти цифры всегда преподносятся как шокирующие, нарушающие нормальный порядок вещей, будто ситуация, в которой деньги или сообщения не распределяются линейно, в наивысшей степени неожиданна. Но ничего неожиданного в этом нет. Вернее, не должно быть.
Итальянский экономист Вильфредо Парето столетие назад выяснил, что в разных странах мира наиболее состоятельные 25% населения контролировали большую часть богатства. Следствия феномена, обнаруженного Парето, известны под множеством имен: правило 80/20, закон Ципфа, распределение по степенному закону, принцип «победитель получает все» — но модель распределения всегда одна: самые богатые, деятельные, имеющие больше всего связей участники системы отвечают за состояния, действия или количество связей, в разы превышающие средние показатели.
Кроме того, данная схема рекурсивна (рекурсия — способ общего определения множества объектов или функций через себя, с использованием ранее заданных частных определений. — Esquire). Это означает, что внутри верхних 20% системы, обнаруживающей распределение Парето, в свою очередь есть свои верхние 20%, которые дают непропорционально больший результат, чем остальные 80%. И так далее. Элемент, который находится на верхушке такой системы, будет обладать гораздо большим весом, чем все остальные (так, в английском языке слово «the» является не только самым распространенным, но и встречается в два раза чаще, чем второе по частоте употребления слово «of»).
Пример распределения Парето

Схема, обнаруженная Парето, оказалась настолько распространенной, что он назвал ее «предсказуемым несоответствием». Впрочем, он был слишком оптимистичен — даже сто лет спустя мы не научились предсказывать это вездесущее несоответствие. Отчасти наше неумение ожидать ожидаемого объясняется тем, что нас учат: хрестоматийное распределение больших систем — это Гауссово распределение, общеизвестное в качестве кривой нормального распределения. Например, на кривой нормального распределения роста среднее значение и медиана (срединная точка в системе) совпадают: средний рост ста американок, отобранных случайным образом, составляет около 165 см, при этом, если всех их выстроить по росту, то высота пятидесятой по счету будет 165 см.
Пример нормального (Гауссова) распределения

В распределениях Парето все иначе: рекурсивное долевое соотношение 80/20 означает, что среднее находится далеко от середины. Это, в свою очередь, означает, что в подобных системах большинство людей (или того, что подлежит измерению) показывают результат меньше среднего. У экономистов есть шутка: «Когда Билл Гейтс заходит в бар, то все его посетители становятся, в среднем, миллионерами». Распределение Парето проявляется в удивительно большом множестве сложных систем: ему следует частота тэгов к фотографиям на Flickr, сила землетрясений, популярность книг, размер астероидов и количество контактов у ваших друзей. Этот принцип является настолько базовым для научных исследований, что производится даже специально разлинованная бумага, показывающая распределение Парето в виде прямых линий.
Но несмотря на то что науке все это известно уже сто лет, примеры распределений Парето регулярно представляются общественности как аномалии, мешающие ясному видению мира. Мы должны отказаться от мысли, что средний семейный доход и доход средней семьи имеют что-то общее и что самое большое землетрясение или падение на рынке в будущем окажется сопоставимо с самой масштабной катастрофой в прошлом. Чем дольше существует система, тем выше вероятность события, которое в два раза превосходит все предшествующие.
Это не означает, что мы никак не можем воздействовать на такие распределения. Снижение кривой Парето от «головы» к «хвосту» может быть более или менее резким. Иногда политическое или социальное вмешательство способно повлиять на крутизну кривой — налоговая политика может повысить или снизить долю дохода 1% самых богатых жителей страны. Но пока мы не признали, что есть множество систем, в которых действует распределение Парето, и что они останутся таковыми всегда, мы даже не начали их осмысливать. Вероятно, мы просто пытаемся надеть на «корову» Парето «седло» Гаусса. Сто лет спустя после открытия «предсказуемого несоответствия» мы должны довести дело до конца и все-таки начать его предвидеть.
1 комментарий
+++
- 30 января 2012, 16:51

теги блога Александр Дрозд
- 2012
- bitcoin
- wealth lab
- акции
- алгоритм
- алгоритмическая торговля
- алгоритмы
- алготрейдинг
- Американский рынок
- аналитика
- аналитики
- биржа
- биткоин
- вероятность
- внутридневная система
- волатильность
- выборка
- Горчаков
- грааль
- Греция
- деньги
- дефолт
- диверсификация
- доходность
- доходы
- ДУ
- еврозона
- европа
- жадность
- золотые слова
- идеи
- инвестиции
- итоги месяца
- итоги сентября
- китай
- комиссия
- крах евро
- кризис
- криптовалюты
- кукловоды
- лайткоины
- ЛЧИ
- математика
- математическое ожидание
- Миловидов
- мобильный пост
- модель
- мультфильм
- мысль
- нефть
- октябрь
- опрос
- опыт
- оффтоп
- плечи
- плюсики
- польза обществу
- потери
- прогнозы
- программирование
- просадки
- проскальзывание
- психология
- рейтинг
- ренко
- РИ
- риск
- риски
- робот
- роботы
- ртс
- рынки
- рынок
- система
- системная торговля
- системный трейдинг
- системы
- смартлаб
- статистика
- Стратегии
- стратегия
- страх
- сша
- технический анализ
- топики
- торговая система
- торговые системы
- трейдеры
- трейдинг
- управляющие
- физика
- финансы
- фондовый рынок
- фьючерс
- фьючерсы
- хэдж фонд
- Ценная подборка
- шум
- эквити
- экономика


















