Блог им. AGorchakov |Мои итоги сентября и квартала
- 01 октября 2021, 09:35
- |
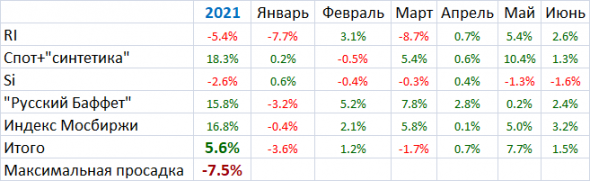
Начнем с традиционной таблицы
Пропустить такие тренды, которые были в RI и GAZP c 27 августа по 15 и 30 сентября, соответственно, для моих систем было бы «преступлением». Они его и не совершили.
( Читать дальше )
- комментировать
- ★2
- Комментарии ( 30 )
Блог им. AGorchakov |Новичкам на память (просто "достало")
- 08 сентября 2021, 09:55
- |
Типичный диалог на трейдерских ресурсах:
«Трейдер». Мой прогноз сбылся на все 100 (ссылка на один из кучи «прогнозов»), я на нем заработал кучу бабла. А Вы так можете?
Скептик. Весь стейтмент хотя бы лет за 5 покажи.
«Трейдер». Зачем? Я в ДУ не беру!
Новички – запомните, кавычки у слова «трейдер» тут поставлены мной совсем не случайно.
P. S. В комментариях как раз и четко сформулировали суть поста: "не следуйте сигналам тех, кто не доказывает стейтом доходность своей торговли, какими бы успешными их трейды не казались в единичных случаях." Спасибо PrAct.
Блог им. AGorchakov |Пустячок, а приятно
- 03 сентября 2021, 18:05
- |
Но, с другой стороны, как я уже писал прошлым летом, отставание этого индекса от индекса Мосбиржи с начала года свидетельствует об отсутствии интереса к нашему рынку со стороны реальных нерезов.
На 18:45 02.09.2021
Индекс RST +15.94%
Индекс Мосбиржи +21.34%
Сравнение корректно, так как оба индекса чисто ценовые без учета дивидендов.
Для сравнения динамика индексов в октябре-декабре прошлого года, когда реальные нерезы приходили:

Не удивляйтесь результатам октября: приход реальных нерезов в 90%+ случаев предваряет коррекция рынка вниз с последующей «ракетой».
Повторится ли осень 2020-го в 2021-м? Ох, не знаю, это из серии «знал бы прикуп, жил бы в Сочи». Октябрь покажет.
Блог им. AGorchakov |Мои итоги августа
- 01 сентября 2021, 10:00
- |
Начнем с традиционной таблицы
Когда я думал над комментариями в первой половине третьей декады августа, то планировал их начать с фразы: главным неудачником августа стал RI-тренд. Собственно так оно и было: он получил две большие «пробоины» 6 и 9 августа и «героически» отбил около 70% того убытка, что позволило прибыли RI-контртренд перекрыть текущие убытки RI-тренд. Все резко изменилось после речи Пауэлла в Джексон Холле 27-го. Лонги в RI-тренд, открытые в течение некоторого времени после нее в этот же день, дали прибыль практически равную убыткам 6 и 9-го и, соответственно, вывели RI-тренд в хороший плюс, даже чуть больше августовского плюса в RI-контртренд. Зато Si получил большую «пробоину» и из небольшого плюса ушел в минус и по летней традиции этого года стал единственным неудачником августа.
В результате в августе счет сделал несколько раз новые исторические максимумы и закончил август на историческом максимуме, что, как я уже писал в июльском обзоре, не характерно для августа в моей торговле. И вообще три летних месяца в плюс я последний раз имел в 2017-м году ( с 2002-го по 2016-й такое было только еще один раз в 2003-м, а до июля 2002-го у меня просто нет помесячной статистики счета).
( Читать дальше )
Блог им. AGorchakov |Пятничное
- 06 августа 2021, 17:36
- |

И успокаивает только одно: всего с 04.10.2007 на этот счет было внесено чуть меньше 1,5 млн. руб.: 266 327 руб. - 04.10.2007 (почему такая кривая цифра об этом в истории ниже) и по 400 тыс. в марте 2008, январе 2010 и марте 2012-го. Выводов не было, если не считать удержаний НДФЛ.
Как получилась первая кривая цифра? Летом 2007-го Церих предложил всем желающим вести публичные счета с очень «сладкой» комиссией: 0,01% от оборота при любых суммах и оборотах и 16% годовых за плечи и шорты. Риск-Инвест решил этим воспользоваться и выставить на публичное обозрение свою торговлю. Решили торговать две стратегии: RITS классическая (как у клиентов) и RITS агрессивная (экспериментальная под любителей «американских горок»). Счета решили сделать небольшие — по 300 тыс. и свои деньги на них дали я и гендиректор. Гендиректор мне предложил выбрать стратегию, я предложил жребий и по жребию мне досталась RITS агрессивная.
( Читать дальше )
Блог им. AGorchakov |О важности периода представления результатов
- 04 августа 2021, 13:54
- |

Вроде все нормально и показательно. А теперь давайте разобьем этот период на два: до 18.03.2020 и после. Что получим?
ДО

( Читать дальше )
Блог им. AGorchakov |Диверсификация - "наше Фсе"!
- 03 августа 2021, 13:05
- |
Посчитал характеристики индекса Gorchakoff Global index с момента создания (чистый out of sample, хотя и ранее доли не оптимизировались, только отбор стратегий был).
Из 31 месяца только три убыточных: ноябрь 2019, февраль и октябрь 2020-го.
А числовые характеристики в рублях по подневной динамике счета выглядят так:

По моему мнению, эти цифры — лучшее доказательство утверждения, что диверсификация по инструментам, методам торговли, спекуляциям и инвестициям, странам — это лучший и единственный метод ограничения рисков и получения качественного соотношения «доходность-риск».
P. S. Для сравнения аналогичные цифры для моего счета за тот же период

Это к вопросу «одна голова — хорошо, а две лучше».
Блог им. AGorchakov |Почему я стал публиковать свои результаты
- 31 июля 2021, 17:10
- |
Началось это в далёком 2002-м году, когда в компанию, где я тогда работал, стали приходить клиенты, которые ничего не знали ни обо мне, ни о моем управлении, но слышали, что на акциях можно хорошо заработать.
До 2002-го я торговал всего на 5-ти счетах: компании, своем (записан на жену) и трёх клиентов. Из этих трёх клиентов один был моим хорошим знакомым, а два других — родные братья, которым меня рекомендовал наш общий знакомый.
Естественно, что со стороны новых клиентов при первом месячном минусе началось роптание, вплоть до обвинения со стороны одного клиента в переливе, на том основании, что в присланном отчёте у него куча убыточных сделок и наверняка мы были контрагентом.
Что делать? Решение с моей стороны созрело быстро: утром, в первый рабочий день следующего месяца на сайте компании публикуем результат в процентах на счете компании за месяц и с начала года. Если у клиента претензия, а результаты отличаются не более, чем на 0,2%, то предлагаем просто заглянуть в сообщение и убедиться, что «мы в одной лодке». Упомянутая выше часть вопросов отпала.
Потом по моему предложению добавили ещё один показатель: максимальная просадка с начала года, правда, по опыту общения с действующими клиентами и потенциальными, он мало кого интересовал. Но мне так было спокойнее.
Но возникла новая проблема: «рынок +2%, а счёт -2%» (в обратной ситуации почему то претензий не было). Как быть?
Опять решение созрело быстро: добавить в сообщение краткий комментарий управляющего на чем заработали и почему проиграли. Так и «пошло-поехало».
В Риск-Инвесте ещё до моего прихода скопировали эту идею (не удивительно, если я был знаком с его директором ещё по общению на форуме аналитиков РТС в 1999-2001 и первую встречу в реале посетителей форума howtotrade в январе 2003-го организовал он) и потому я туда пришел в 2004-м «на все готовенькое».
Даже когда в 2008-м нам босс запрещал иметь сторонних клиентов, я все равно написал полугодовой обзор результатов на своем счёте
www.howtotrade.ru/nw/index.php?p=1214859528
Были перерывы? Были. В 2012-2013-м шла «перестройка» и мне ничего не хотелось писать и я только в закрытой части форума howtotrade продолжал публиковать результаты в формате:
02.11
( Читать дальше )
Блог им. AGorchakov |Мои итоги июля
- 31 июля 2021, 09:29
- |
Начнем с традиционной таблицы
Как видно из таблицы, основная прибыль июля пришлась на RI, точнее на RI-тренд (RI-контртренд закончил июль в небольшом минусе). Причина очевидна: появились движения в несколько дней в Si и возродилась сильная отрицательная корреляция между RI и Si. А вот сам Si в режиме «лонг с плечом» не «блеснул».
Подводя итог, можно сказать, что для июля (лето, отпуска – «рынок никакой») результат неплохой, но впереди август, самый неприятный месяц в моей многолетней торговле. С 2006-го года, включительно, я могу вспомнить только один очень удачный август – август 2017-го, когда счета под моим управлением «рывком» вышли из просадки, длившейся с марта 2016-го. Но, увы, это была лишь моя маленькая «победа», не отразившаяся в итоге на судьбе Форума. Удачным мог бы быть и август 2011-го, но тот год был «годом упущенных возможностей». А неудач именно в августе было гораздо больше:
( Читать дальше )
Блог им. AGorchakov |Мои итоги июня и полугодия
- 01 июля 2021, 09:58
- |
Начнем с традиционной таблицы
14 июня был достигнут новый исторический максимум счета, в первую очередь за счет RI-тренд, через который удалось поймать шорт в Si или лонг в индексе Мосбиржи. В то же время сам Si после нескольких неудачных попыток сыграть в лонг с 18.06 был «вырублен» «фильтром большой пилы», вообще запрещающим любую торговлю. В акциях были разные тенденции:
— в SBER весь месяц был включен «фильтр малой пилы» (1 система из 4-х в лонг и шорт по всем системам на 1/3 лимитов лонга) и его действительно «пилило»;
— в GAZP торговался только лонг с плечом и получился плюс в июне;
— в GMKN торговался лонг+шорт без плеча, при этом лонги минусовали, а шорты плюсовали, но из-за разницы в объемах (шорт=1/3 лонга) по итогам месяца получился минус.
В целом после исторического максимума счет за три дня 15-17 июня попал в просадку в 2,7%, после чего «лег в дрейф» до 28 июня, включительно, и «распилился» на движениях вниз-вверх 29-30-го, добавив к просадке еще примерно 1%.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс