SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
Избранное трейдера Стас Бржозовский
Нобелевская премия по экономике за 2013 и проблемы фондового рынка.
- 06 ноября 2013, 10:18
- |
Присуждение нобелевской премии по экономике Юджину Фаме, Роберту Шиллеру и Ларсу Питеру Хансену возобновило дискуссии об эффективности и границах применимости краткосрочных и долгосрочных прогнозов. Так как предложенная Ю. Фамой идея информационной эффективности рынка, по сути, есть другая формулировка главной аксиомы теханализа – цены учитывают все, а подход Р. Шиллера опирается, прежде всего, на результаты работы компании (отношение дивидендов к цене), то эта дискуссия, по сути, представляет собой спор сторонников фундаментального и технического анализов. Первый подход активно развивается УК «Арсагера». Их точка зрения представлена на площадке смарт-лаба блогом http://smart-lab.ru/my/Arsagera/. Сторонников технического анализа гораздо больше и выделить кого либо, кто персонифицировано выражает эту точку зрения сложно.
Эта дискуссия началась в блоге http://smart-lab.ru/blog/145649.php. Однако продолжения не получила.
( Читать дальше )
Эта дискуссия началась в блоге http://smart-lab.ru/blog/145649.php. Однако продолжения не получила.
( Читать дальше )
- комментировать
- ★13
- Комментарии ( 40 )
Расчёт ГО своими руками.
- 25 октября 2013, 13:15
- |
При данном исследовании было потрачено немало труда, поэтому ссылка на автора при перепечатке обязательна. © Simix.
Сразу скажу что расчёт ГО тема скользкая, т.к. представляет собой величину умозрительную — риск. Есть люди, которые прыгают с парашютом для развлечения, а я считаю что этот риск слишком велик чтобы прыгать без необходимости. То есть риск зависит от того, кто смотрит. Если бы мы все знали реальные риски той или иной ситуации, то была бы не жизнь, а красота. Поэтому ровно такое же ГО как в QUIKе вы не получите никаким оффлайновым алгоритмом. Биржа имеет насчёт ГО свои взгляды, собственные поправочные коэффициенты и собственный модуль, который работает только с подключением к бирже.
Но посчитать ГО в оффлайне всё-таки можно.
Чтобы как-то ограничить и описать риск количественно, биржа вводит ряд предположений и условий, а также приводит открытую методику которыми мы и воспользуемся:
( Читать дальше )
Сразу скажу что расчёт ГО тема скользкая, т.к. представляет собой величину умозрительную — риск. Есть люди, которые прыгают с парашютом для развлечения, а я считаю что этот риск слишком велик чтобы прыгать без необходимости. То есть риск зависит от того, кто смотрит. Если бы мы все знали реальные риски той или иной ситуации, то была бы не жизнь, а красота. Поэтому ровно такое же ГО как в QUIKе вы не получите никаким оффлайновым алгоритмом. Биржа имеет насчёт ГО свои взгляды, собственные поправочные коэффициенты и собственный модуль, который работает только с подключением к бирже.
Но посчитать ГО в оффлайне всё-таки можно.
Чтобы как-то ограничить и описать риск количественно, биржа вводит ряд предположений и условий, а также приводит открытую методику которыми мы и воспользуемся:
( Читать дальше )
Откуда возникает улыбка волатильности?
- 17 августа 2013, 21:55
- |
Продолжая популярную сейчас тему с моделями улыбки волатильности, хочу поделиться результатами своего исследования на эту тему. Немного стремно делать это после поста Виталия Курбаковского. Но может кому-то и мое исследование будет интересно. Сам я не математик и не трейдер, просто программист. Поэтому не судите строго.
Наблюдая за поведением улыбки волатильности, уже давно мучали вопросы: Почему улыбка поднимается то вверх, то вниз? Почему она изогнута именно так, а не иначе? Почему перекатывается за текущей ценой БА, причем дно улыбки справа от БА и только к экспирации подтягивается к БА и улыбка становится симметричной? Почему ветви у нее то поднимаются, то опускаются? И главный вопрос: Что является причиной возникновения улыбки волатильности? В некоторых источниках утверждают, что улыбка возникает из-за толстых хвостов распределения приращений. Решил проверить это и провести небольшое исследование.
Насколько понял теорию вопроса, чтобы посчитать свою улыбку волатильности, нужно иметь распределение вероятностей, какой будет цена БА на экспирацию (в дальнейшем — распределение цен). Если знать это распределение, то можно однозначно вычислить цены опционов на каждом страйке, и потом, используя формулу Блека-Шоулза, можно вычислить IV на каждом страйке, и получить улыбку волатильности. Как можно получить распределение цен? Решил построить его, генерируя тысячи случайных траекторий цены, начиная с текущего значения БА. Конечные точки траекторий (цена БА на экспирацию) сохраняю, и в конце смотрю, как часто цена попадала в тот или иной диапазон. Так получаю распределение цен на экспирацию. Для построения случайной траектории решил использовать распределение приращений, которое реально было на рынке (в дальнейшем — эмпирическое распределение). Вот, например, распределение приращений (на минутках) для фьючерса RTS-9.11:
( Читать дальше )
Наблюдая за поведением улыбки волатильности, уже давно мучали вопросы: Почему улыбка поднимается то вверх, то вниз? Почему она изогнута именно так, а не иначе? Почему перекатывается за текущей ценой БА, причем дно улыбки справа от БА и только к экспирации подтягивается к БА и улыбка становится симметричной? Почему ветви у нее то поднимаются, то опускаются? И главный вопрос: Что является причиной возникновения улыбки волатильности? В некоторых источниках утверждают, что улыбка возникает из-за толстых хвостов распределения приращений. Решил проверить это и провести небольшое исследование.
Насколько понял теорию вопроса, чтобы посчитать свою улыбку волатильности, нужно иметь распределение вероятностей, какой будет цена БА на экспирацию (в дальнейшем — распределение цен). Если знать это распределение, то можно однозначно вычислить цены опционов на каждом страйке, и потом, используя формулу Блека-Шоулза, можно вычислить IV на каждом страйке, и получить улыбку волатильности. Как можно получить распределение цен? Решил построить его, генерируя тысячи случайных траекторий цены, начиная с текущего значения БА. Конечные точки траекторий (цена БА на экспирацию) сохраняю, и в конце смотрю, как часто цена попадала в тот или иной диапазон. Так получаю распределение цен на экспирацию. Для построения случайной траектории решил использовать распределение приращений, которое реально было на рынке (в дальнейшем — эмпирическое распределение). Вот, например, распределение приращений (на минутках) для фьючерса RTS-9.11:
( Читать дальше )
Обобщенная модель стоимости опционов
- 15 августа 2013, 18:37
- |
Я давно обещал выложить в сеть свою статью из журнала FO с обобщенной моделью стоимости опционов, что сейчас и делаю
Сначала некоторые замечания к статье, ниже она сама
Обобщенная модель (ОМ) создавалась как упрощенная версия классической модели Блэка-Шолеса (БШ) для автоматической торговли опционами. Впоследствии оказалось, что главное достоинство ОМ состоит в том, что она позволяет обойтись без введения в рассмотрение понятия кривой волатильности (IV) и от всех последующих неприятностей, связанных с необходимостью ее анализа и прогнозирования.
Основная идея ОМ продемонстрирована на рисунке (Рис.1). Ожидаемая подвижность m ATM опционов, связанная с ценой формулой (6), есть линейная функция цены Fбазового актива (БА).
( Читать дальше )
Толстые хвосты и эмпирические распределения. Продолжение
- 14 июня 2013, 11:32
- |
Продолжаю тему, поднятую в статье «Толстые хвосты и эмпирические распределения». Напоминаю, в материале рассматривался вопрос, как влияют толстые хвосты распределения цены базового актива на появление улыбки волатильности. В представленной модели фьючерс РТС каждый день прыгает на величину, случайно выбранную из ряда его ежедневных приращений в прошлом. Ранее были показаны результаты модели для 100 шагов движения цены. К ним мы еще вернемся, а пока рассмотрим, что происходит при небольшом количестве шагов модели. В этом случае, Центральная Предельная Теорема только начинает работать, и толстые хвосты разворачиваются во всей своей павлиньей красе.
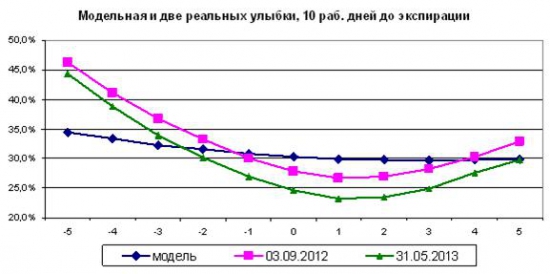
Выше представлена модельная улыбка за 10 дней и две реальных кривых волатильности опционов с аналогичным сроком жизни. Как и раньше, в модели введена поправка на тренд. По оси Х номер страйка от центрального, графики совмещены по горизонтали.
( Читать дальше )

Выше представлена модельная улыбка за 10 дней и две реальных кривых волатильности опционов с аналогичным сроком жизни. Как и раньше, в модели введена поправка на тренд. По оси Х номер страйка от центрального, графики совмещены по горизонтали.
( Читать дальше )
Толстые хвосты и эмпирические распределения
- 06 июня 2013, 15:15
- |
Финансовые рынки обладают известным свойством – толстые хвосты в распределении приращений актива. Обычно, для демонстрации эффекта сравнивают два графика дневной доходности – для исторического распределения цен и нормального. На рисунке ниже четко заметны выбросы в распределении доходности индекса вдалеке от центра.

Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в начальной точке, ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже

( Читать дальше )

Часто можно услышать, как толстые хвосты назначают главной причиной возникновения улыбки волатильности. На недавно прошедшей НОК одним из наиболее интересных выступлений была презентация Виталия Курбаковского о причинах появления улыбки волатильности. Уважаемый мэтр строил улыбку на основе эмпирического распределения.
Проверим сами, как влияют толстые хвосты на форму улыбки. Построим модель движения фьючерса РТС на основе данных о ежедневной доходности close to close основной сессии. Возьмем ряд ежедневных приращений склеенного фьючерса с января 2010г. по февраль 2013г. Конечное значение цены близко к начальному, но, чтобы совсем исключить тренд, последнее значение цены фьючерса примем равным первому, а именно 157090 п. Период модели – 100 дней. Каждый день актив прыгает на величину, случайно выбранную из ряда прошлых значений. В конце траектории посчитаем стоимость опционов. Повторим опыт миллион раз. Усредним результаты каждого опыта и получим ожидаемую стоимость опционов в финальной точке. Она совпадает со справедливой стоимостью опционов в начальной точке, ведь ставка равна нулю. Результат моделирования в терминах волатильности представлен ниже

( Читать дальше )
Покупать или продавать?
- 23 ноября 2012, 10:12
- |
Верно ли утверждение:
«Если самому себе выписать опцион, то при правильном управлении соответствующими стратегиями можно заработать, ничем не рискуя»?
Напишите, кто что думает по этому вопросу. Торговый опыт и знания мат. базы значения не имеют. Приветствуется любая точка зрения. Троллей и им подобных попрошу быть поздержанней. Топик написан с целью развить тему выбора стратегии, чтобы каждый для себя вынес из неё что-то полезное!!!
«Если самому себе выписать опцион, то при правильном управлении соответствующими стратегиями можно заработать, ничем не рискуя»?
Напишите, кто что думает по этому вопросу. Торговый опыт и знания мат. базы значения не имеют. Приветствуется любая точка зрения. Троллей и им подобных попрошу быть поздержанней. Топик написан с целью развить тему выбора стратегии, чтобы каждый для себя вынес из неё что-то полезное!!!
Опционный зигзаг в тезисах
- 19 ноября 2012, 15:06
- |
В околоопционном информационном пространстве широко представлены описания классических опционных стратегий. Но стратегия, описанная ниже упоминается редко или вообще не упоминается, хотя в последнее время вызывает всё больше интереса и споров. Когда-то решил тезисно набросать мысли по ней – сейчас файлик попался на глаза, почистил, обновил и выложил. Не имея математического образования, заранее прошу прощения за отсутствие сложных математических выкладок, вызывающих у меня стойкий рвотный рефлекс. Всё написанное ниже носит скорее интуитивный характер, никаким боком не претендует на истину ”в последней инстанции” и выложено с целью сподвигнуть народ на комментарии и дополнения по существу (комментарии типа “нутыимудак” и “самтопонял чонаписал”, если можно, направляйте сразу в личку)
Опционный зигзаг в тезисах
( Читать дальше )
Опционный зигзаг в тезисах
( Читать дальше )
Арбитраж. Деньги без риска.
- 17 ноября 2012, 13:57
- |
Рассмотрим простейший случай арбитража акция –фьючерс. Возьмём, к примеру самую голубую фишку.
Сегодня 18 июня 2012 время 10:05
ГАЗПРОМ –157.57, за пучок 15757 руб.
GZZ2 — 16008 руб.
И разница между ними 251 руб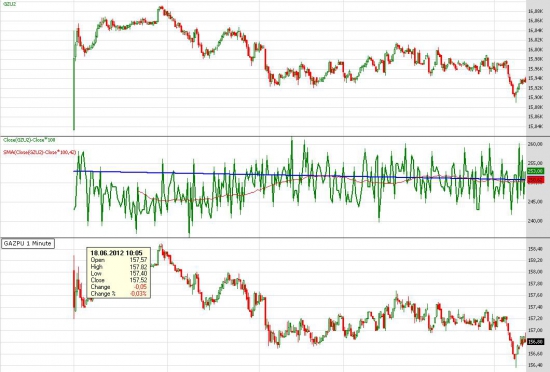 .
.
Синяя линия это наш ожидаемое движение, а зеленый шум реальное движение разницы.
Прошло три месяца и вот уже 13 сентября время 18:22
ГАЗПРОМ –162.50, за пучок 16250руб.
GZZ2 – 16252 руб.
И разница между ними 2 руб.
Итого мы заработали примерно 250 руб. Что составляет примерно 0,5% в месяц или 6% годовых.
Как заработать больше? Нужно делать больше сделок продавая дорого и покупая дешевле. Проведем среднюю с периодом 42 бара (от этой величины результат зависит слабо). Красная линия. И будем входить выше средней на 4 руб, а выходить на 4 руб ниже. И за какие то 15 сделок в день получим 3180 руб. (около 6,5 % в месяц).
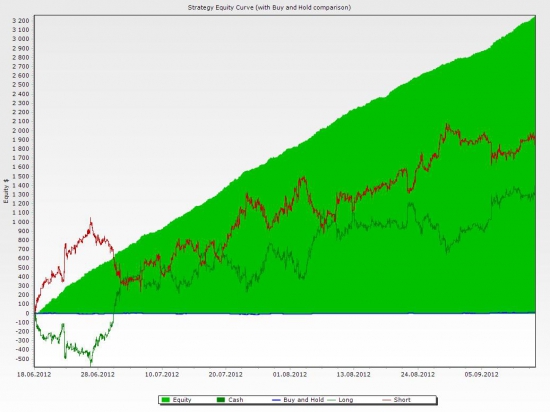
( Читать дальше )
Сегодня 18 июня 2012 время 10:05
ГАЗПРОМ –157.57, за пучок 15757 руб.
GZZ2 — 16008 руб.
И разница между ними 251 руб
 .
.Синяя линия это наш ожидаемое движение, а зеленый шум реальное движение разницы.
Прошло три месяца и вот уже 13 сентября время 18:22
ГАЗПРОМ –162.50, за пучок 16250руб.
GZZ2 – 16252 руб.
И разница между ними 2 руб.
Итого мы заработали примерно 250 руб. Что составляет примерно 0,5% в месяц или 6% годовых.
Как заработать больше? Нужно делать больше сделок продавая дорого и покупая дешевле. Проведем среднюю с периодом 42 бара (от этой величины результат зависит слабо). Красная линия. И будем входить выше средней на 4 руб, а выходить на 4 руб ниже. И за какие то 15 сделок в день получим 3180 руб. (около 6,5 % в месяц).

( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал