Наверное, если кто сможет сгенерировать реальную волу, а значит, в обратную сторону, получить формулу ее расчета, тот получит следующую Нобелевскую премию. А я и не претендую (зачем мне она, «Мы делаем деньги на бирже»). Для начала давайте обсудим и согласуем свойства волатильности. Скачиваем файл.

https://cloud.mail.ru/public/k69C/4k8khnUhR

Что мы обычно делаем. Берем приращения логарифмов, потому что мы знаем, что цена растет по экспоненте. И из этих приращений делаем распределение. И мы допустим, что это распределение может быть нормальным от Гауса. Поэтому мы сразу нагенерим такую последовательность, которую нам выдавала в формуле sigma*W. И которую мы извлекаем из БА.

Сгенерируем нормальное распределение. В прошлый раз мы брали просто случайные числа для волатильности. Для того что бы сделать их числами нормального распределения надо вставить в функцию из эксела, «нормальное обращение» и задать волатильность нормальности и среднее. Смотрите формулу на листе «Нормальное распределение». Среднее мы оставим 0 волу 0,2. Если еще, кто ни будь не видел, то вот оно, о чем тут такие жаркие споры. При каждом пересчете выдаются параметры этого распределения. СКО и оно соответствует заданному 0,2. Эксцесс около 0 и Скос около 0. То есть выдерживаются все параметры Гауса. Ниже график дисперсии. Наши  «дельта индикатор» и график волатильности со средней 20, который ходит вокруг 20. Вы можете пересчитывать лист. Распределение посчитано за 200 периодов, так что оно немного гуляет. И это нормально. У нас не так много значений в анализе.

( Читать дальше )

Давайте соберем цену, потом разберем цену и сравним. Все будет производиться на ваших глазах в экселе. Файл, которого я прикладываю. ФАЙЛ https://cloud.mail.ru/public/27GB/5ipstzGrY  .(в зеленые области вы будите вписывать разные цифры).  Проверку на гетероскедастичность мы будем делать методом максимального правдоподобия. Во я загнул. Если просто. Мы возьмем две, хорошо известных нам стратегии и будем их прогонять на каждом шаге создания графика цены. Первая стратегия. Увеличение лота на один при убытке. Принцип опциона. И если у нас случайный процесс, то должно получаться 50/50. И удвоение позиции. Принцип мартингейта. И если у нас случайный процесс у=x^2, то у^2=x, мы всегда в плюсе. Давайте по шагам.

Шаг первый, лист W

Сгенерируем случайные числа. В экселе есть функция =случмежду(0;1). И 0 переведем в -1, а 1 в 1. У нас получился простой бинарный ряд из 1 и -1. Возьмем 100 таких цифр. Теперь посчитаем их сумму нарастающим итогом.  К сумме предыдущей прибавить следующее (Total). И построим график изменения этой суммы. Назовем это «геометрическое Броуновское движение».  Тогда, сумма всех случайных числе будет равна точке, куда пришел наш график. А сумма всех случайных чисел в квадрате, будет равна пройденному пути. А если каждый шаг происходит за 1 секунду. То это, одновременно, и время. И мы должны получить следующую зависимость. Берем 100, извлекаем корень квадратный и получаем 10. И это одно стандартное отклонение. И есть теорема, которая доказывает, что 68% траекторий  будут заканчиваться в диапазоне от -10 до +10. Вы можете это проверить сами. В графе ТЕСТ введите число. Если сумма средних от -10 до +10, ставим 1, если больше 0. У вас будет получаться среднее 0,7, в среднем. То есть в 3 случаях из 10 мы будем выскакивать из -10 +10. И это уже не 50/50 вверх или в низ. Это уже 30/70.

( Читать дальше )

Был такой дядька. Киёси Ито. Работал в статистическом  управлении и писал книжки. Интернета тогда не было, поэтому он, как и Тимофей Мартынов, делал книжки из бумаги и писал в них ручками. Писал он о теории вероятности и стохастике, то есть про кроликов, и внимание. За эти работы он получил степень доктора философии. То есть, тут не столько вопрос в математике, сколько в философии.

Дифур это такой способ записи философской мысли. Когда вы рисуете каналы по лоу на графике, вы даже не задумываетесь, что это касательная, а значит производная функции цены от времени. Для записи мысли или идеи мы воспользуемся дифурами, а потом переведем их. В общем, их особо ни кто не решает. Берут справочник производных и вуаля.  dx/dt = α x => x(t) = x0 e^αt. Уравнение разряда конденсатора dx/dt.  У каждого уважающего опционщика такой справочник есть. Это греки опционов. Там дифур и его значение в обычной формуле, куда можно уже цифры подставить. И все.

Из предыдущего материала мы помним. dx = µ x dt + σ x δW. Мгновенное изменение цены=среднему изменению+размеру изменения*случайное изменение. Давайте этим философским языком пообщаемся. И легче всего это понять методом Кирилла Ильинского.

( Читать дальше )

Когда имеешь график функции, такой как опционные цены, то можно подобрать функцию которая ляжет на этот график. У меня есть целая коллекция таких функций. Но я вам хочу представить функцию, которой можно дать объяснения и потом долго доказывать, что она правильная.

В природе много различных процессов, которые математически описываются одними и теми же математическими формулами.  Возьмем за основу процесс, график которого очень схож с прайсингом опционов.

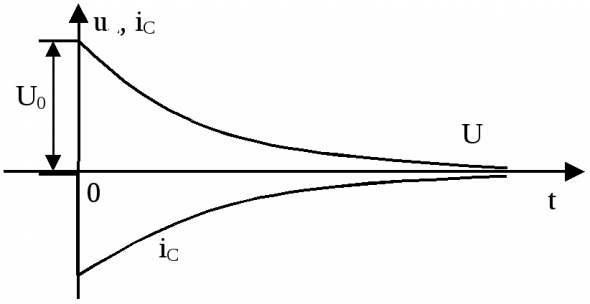
( Читать дальше )

Хорош философствовать. Давайте писать более полезные посты.
Итак, робот на двух графиках Боллинджера.
Общий принцип:
1) На цену накладываются два графика Боллинджера: с периодами 20 и 120 (назовем их local и global).
2) В зависимости от параметра внутри робота, входим либо когда цена входит внутрь local-Боллинджера (ContrTrendFlag=1), либо выходит из него (ContrTrendFlag=0).
3) Дополнительный фильтр: Лонг только когда когда мы в верхней половине global-Боллинджера, шорт — если в нижней.
Данные робот берет из графиков, так что график должен быть открыт, и прописаны идентификаторы.

График с двумя Боллинджерами выглядит примерно так:



Настройки на цене и индикаторах не забудьте:



( Читать дальше )

Давайте не бегать по Блекам и Мертонам, а обратимся к нашим. Андрей Колмогоров из города Тамбов. Родившись еще при царе и прожив в СССР на бирже поторговать не успел. Но написал пару книг по которым учились Блек Шоулз и Мертон. Мощный дядька. Поэтому пойдем по его логике, аксиоматике теории. Она, примерно такая. Святая троица. Пространство элементарных событий. Которые уже не поделишь. Один тик. Цена или вверх или вниз. Одновременно не возможно. Если таких событий много, то мы получим Распределение вероятности. Множество всех возможных исходов. И сигма алгебра. Это какие математические действия мы с ними будем делать и что получать. Вот мы с этой сигмой-алгеброй и попробуем разобраться.

Для этого надо определиться, что нас интересует. Или должно интересовать. Цена? Лично меня не интересует. Вот есть цена Магнит АО. Пока у меня нет этих акций, то для чего мне знать их цену? Если только знать, на сколько я могу купить. А после того, как я их куплю, цена мне тоже не интересна. Мне интересна доходность моего вложения от начала до конца за время Т-Т0. А это есть изменение цены. Поэтому мы больше цену трогать не будем, а будем работать с ее изменениями и нашей доходностью. Изменение цены мы посчитаем через сигма-алгебру. А именно разница логарифмов. В предыдущем топике я описал почему. И получится очень удобно. Доходность +1% умножить на вложенный капитал= фин рез. Цены самого актива тут нет. Вот такой парадокс сигма-алгебры. Теперь нас интересует наш вложенный капитал и изменение доходности.

( Читать дальше )

Смотрю, зацепило. Зацепило про случайность в рынке. Ну оно и не мудрено. Вроде есть тренды, предсказуемость, треугольники и волны, а вот заработать не получается. Ну этому есть объяснение. Причем это связано со случайностью и еще одним аргументом. Называется это Арбитражный аргумент. Если коротко. Если вам, как токарю, предложат 25 тыс на одном заводе и 26 тыс на другом, то вы выберете второй. Если на акциях можно заработать 30%, а на облигациях 10%, то нахрен кому нужны эти облигации. Что бы понять этот процесс надо разобраться со стратегией Маркет Мейкера. Который, как вы думаете, гоняет цену по рынку. Прежде всего, это не так. К ММ приходит случайный пассажир и просит оказать ему услугу по покупке или продаже. При этом ММ все равно, так как он может сразу дать две цены, покупка и продажа. 101 и 99. Не обращая внимания ни на треугольники ни на тренды ни на волны Вульфа. Такая у него работа. Он же не может сказать: «подожди у меня тут треугольник, приходи завтра». Ему не важно, куда пойдет цена. Ему важно, что бы вы к нему пришли.

( Читать дальше )

     Появился кусочек времени — открою кусочек тайны.

     Вчерась я наваял стартовый пост с зачатками идеологии попытки взять своё в виде денех на продаже времени опционного:


Опционы BRENT. Грааль. И снова про ЭТО? «Клубничка». Часть 1.



     В той моей лоховатенькой статейке было несколько пунктов, которые я как бы упустил в прояснении. Начинаю исправляться.


     Вернусь к первоисточнику идеи — я хочу продать временную стоимость, то есть пустой воздух. А дальше что? Правильно — защитить эту продажу (ну или хотя бы часть её). И всё. Игра будет сделана, выигрыш — получен.

     Придётся вносить небольшие уточнения и чуть подробней описывать подход к продаже «воздуха».


     Итак, я хочу продать два спреда — «бычачий» и «медвежачий».
     Почему два — уж один-то из них принесёт бабло! А то и оба!

     Почему именно спреды, в которых количество проданных опционов равно количеству купленных? Чем хуже голая продажа? Оно, казалось бы, вроде не хуже?

( Читать дальше )

Данный пост несёт чисто технический характер.т.к данный текст стерся в шапке моего профиля при попытке правки.Коменты отключил т.к.спор про отсутствие стопов бесконечен.Прошу отнестись с пониманием.Правила для «крепких парней»-слабонервным просьба не следовать и не заморачиваться.Для трейдеров тоже читать вредно однозначно, а следовать  тем более.Мысли заимствованы у многих и это сборная солянка которую я попытался систематизировать.За мысли большое спасибо!

«В очереди на получение доходов от бизнеса держатель акций стоит на последнем месте. Поскольку такие условия рискованны, в среднем он заслуживает более высокого дохода, чем держатели облигаций, которые получают свои деньги обратно первыми.»

                                                                                                                                                                                       Манифест инвестора, Уильям Бернстайн.

( Читать дальше )

Задача с нестандартным решением.

Итак,
у нас есть два шахматиста, выигрывающих с вероятностью p
(и проигрывающих с вероятностью 1-р).

Первый шахматист — игрок эмоциональный,
после очередного выигрыша вероятность выигрыша следующей партии чуть-чуть увеличивается
и равняется p + эпсилон.
После проигрыша вероятность последующего проигрыша
увеличивается на такую же величину.

Второй шахматист — хладнокровный и спокойный,
поэтому ни победа, ни поражение
не меняют у него вероятность выигрыша или проигрыша.

Вопрос:
Какой шахматист окажется более результативным?

PS
Прошлые задачи здесь

smart-lab.ru/blog/491577.php

Одна из них, кстати, так и осталась
непокоренной смартлабовцам...