Все говорят, что нужно инвестировать долгосрочно (15-20-30 лет), а лучше пожизненно. Но никто толком не объясняет, когда же можно перестать пополнять портфель. Ведь инвестируя, мы ограничиваем себя в потреблении сейчас, чтобы больше получить потом. Сколько же лет пополнять портфель? Когда можно начать тратить всю зарплату, ничего не откладывая? Давайте рассчитаем.

( Читать дальше )

К сожалению, у нас в стране люди верят, что самый надёжный способ вложить деньги – это либо положить их на депозит, либо купить недвижимость. Про второй вариант я не буду здесь рассказывать, а по первому расскажу подробно и лаконично.

Уверенность о безрисковости депозита произрастает из одного простого факта — вклады физических лиц до 1.4 млн рублей застрахованы в Агентстве Страхование Вкладов (АСВ), которое в случае банкротства банков организует их погашение, через другие банки примерно спустя 2 недели, и надо сказать – это хорошо, и намой взгляд быстро. Однако, некоторые нечистоплотные банки, принимая деньги на депозит проводят их за балансом, поэтому АСВ их не видит, а пострадавшим приходится ввязываться в достаточно длительные судебные тяжбы, чтобы доказать, что они размещали деньги в этом банке и тоже имеют право на получение денег от АСВ. Судебные тяжбы идут не быстро, и к сожалению, не всегда закачиваются в пользу пострадавших. Поэтому несмотря на наличие государственного страхование, человек может оказаться без денег, и этот риск необходимо учитывать, поскольку он уже делает такие вложения не безрисковыми.

( Читать дальше )

Оформляя сегодня 3НДФЛ на возврат НДФЛа на счет ИИС, подумал, что можно запилить пост.
Итак по по порядку:

1) Заходим в личный кабинет на сайт nalog.ru, через: либо подтвержденную запись на госуслугах, либо через учетную запись полученную именно в налоговой службе.


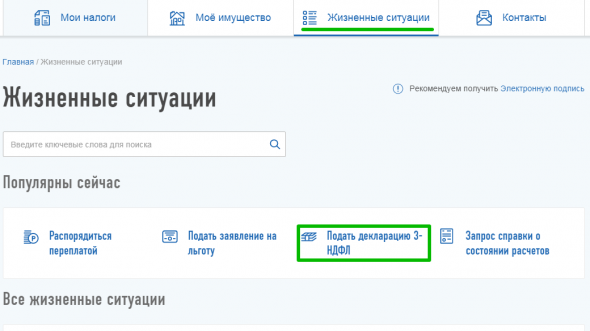
2) Выбираем «Заполнить декларацию онлайн».


( Читать дальше )

Всем привет!
Недавно снял видео где поэтапно показал как можно купить валюту на бирже, а затем вывести ее себе на счет, схему показал с целью экономии для тех кто покупает валюту в обменниках!
У многих на тот момент возник вопрос: «как я собираюсь эти деньги из банка забирать и сколько еще за это заплачу!» 
Сегодняшним постом отвечаю, забрал 1000 долларов купленную по той схеме без каких-либо комиссионных или «удержаний» этих денег на счете! 

Для этого посетил с паспортом ближайший Сбербанк! Комиссия за саму сделку составила 225 рублей, итоговая выгода 1 000 рублей за 1000 долларов(по обменному курсу Сбербанка на день покупки), если брать больше, выгода тоже больше!

Напоминаю в текстом виде простую схему покупки валюты:
1. Заходим в свой сбербанк онлайн, если у вас есть счет в Сбере, если нет идем и открываем любой самый дешевый карточный счет и сразу подключаем себе сбербанк онлайн(далее СО) через банкомат, на всё это у вас уйдет 30 минут!

( Читать дальше )

Господин AlexChi в своем посте Оптимальное количество бумаг в портфеле выложил такую табличку доходностей портфелей акций в зависимости от их количества.



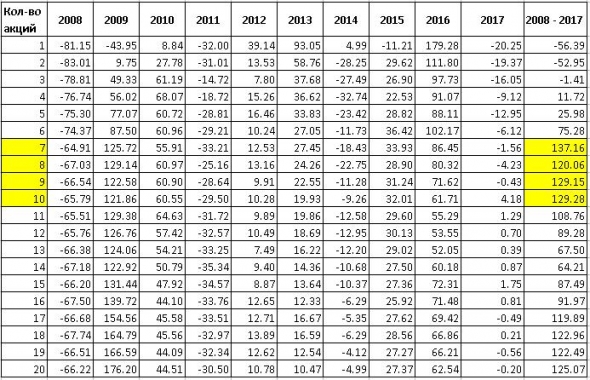
Откинем ошибочную базу рассуждений и посмотрим на сами результаты. Индекс ММВБ за указанный промежуток вырос в номинале всего на 23%. Указанные портфели в разы больше. Классно же!

НО! Даже если откинуть ошибочную статистику, посмотрите на 2014 год. Индекс ММВБ упал за год всего на 8%. А портфели, состоящие из 2-15 акций теряли, порой, в 2-3 раза больше. А если бы индекс упал не на 8%, а на 15%?

Риск всегда обоюден. Кажется, в лучшие годы вы на нем выезжаете, но в худшие годы вас непременно качнет обратно с не меньшей силой. И если риск индекса хоть как-то можно спрогнозировать, то риск одиночных акций — нет и никогда.

З. Ы. Обратите внимание на разброс конечных результатов портфелей из 2-15 акций. От -52% до 137%. То есть, прогнозу не только риск, но и прибыль как элемент риска не поддается.

      Прошлый мой пост я так понял не все поняли. Я чуть расшифрую и немного продолжу.
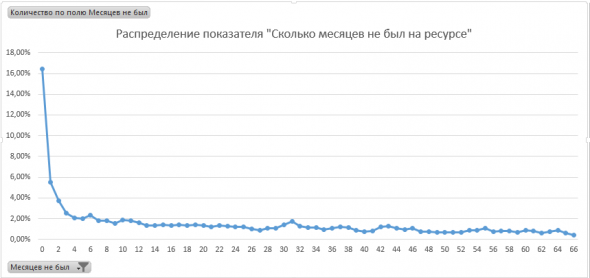
Вот я привел кол-во регистраций по годам. Цифра практически константа, то есть стабильно ~5500 человек

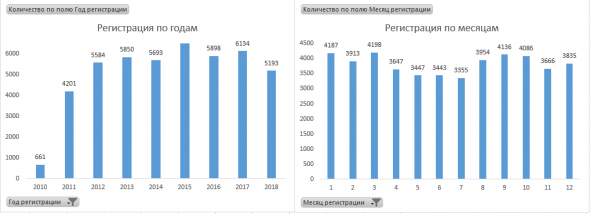
А вот я привел кол-во активных профилей на текущий месяц. Их получилось в районе 16%. То есть порядка 8000 профилей.


( Читать дальше )

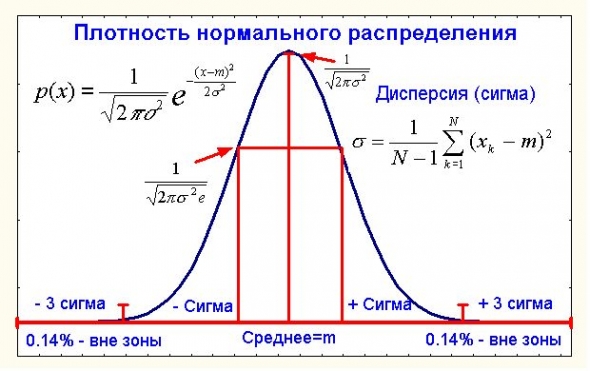
Не подумайте плохого в части нормальности, речь пойдет не о психиатрии, а об известном в теории вероятностей нормальном распределении

 
 

А точнее даже не о нем самом, а об известной центральной предельной теореме (ЦПТ) применительно к ценам.  Что такое центральная предельная теорема в ее классическом виде?

Пусть нам дана некоторая сумма большого числа случайных величин Х=х₁+…+х_N где каждое слагаемое имеет конечную и ненулевую дисперсию (как мы увидим далее в приложении к ценам это условие выполняется). Человечество давно еще с 18 века (Муавр и Лаплас) заинтересовал вопрос распределения случайной величины Х или хотя бы его более-менее точного приближения.

Не будем слишком строги в определениях всяких сходимостей и их скоростей, а сформулируем классическую  ЦПТ в виде интуитивно понятного, но нестрогого термина «близости». Так вот, если x_i – независимы (кто хочет может посмотреть строгое определение независимости, а для менее пытливых скажу только, что корреляция двух независимых случайных величин с конечными дисперсиями – нуль, хотя и обратное не верно), то распределение Х при достаточно больших N практически не отличается от нормального распределения со средним А и дисперсией D, где А – сумма средних x

( Читать дальше )

Давно известно, что если вы хотите купить какую-то акцию дешевле — продайте на нее пут не в деньгах. Например хотите сбер по 180? Продайте 180й пут. Если цена упадет ниже 180 — то вы получите акцию по 180 и еще премию по путу. (например 2) и таким образом эффективная цена покупки будет 178. Ну, а если цена не упала — то получите просто истекшую премию в размере 2, что в пересчете на ГО довольно неплохая доходность. Пример выше — условный, надо смотреть на цены, страйки, волатильность. Но есть одно простое правило — путы лучше продавать тогда, когда рынок уже припал и вола подскочила и часть падения уже пройдена. (Так, сейчас кто-то бросится писать коммент про мой 2008й год. Да, такое бывает. Но сейчас этих предпосылок, вроде как, нет).
Чем еще хорошо продавать путы? что если акция болтается в диапазоне, то вы собираете премию. Обычный владелец стока при неизменной (почти) цене акции получит лишь дивиденды, а вы — опционную премию. (правда не будет дивидендов)

Но тут возникает два момента — первый, с опционами не все знакомы и не все связываются и второй — не на каждый инструмент есть опцион. Поэтому сейчас я расскажу стратегию торговли, для которой не нужны опционы, но суть ее особо не поменяется. Более того, добавятся дивиденды.

( Читать дальше )

Поступила информация, что население смартлаба за последние годы несколько обновилось, и кому-то может оказаться полезным узнать как можно просрать миллиарды на опционах, как можно на салфетках объяснить опционы гуманитарию или как написать робота, который с капиталом 3 млн р держал 15% объемов торгов в опционах RI. В общем иногда полезно перечитывать хорошо забытое старое (сейчас даже сам удивляюсь, как это меня хватило на все это буквосложение)



Гном. Или как трейдер обанкротил банк.

Глава первая и вторая

Глава третья и четвертая

Глава пятая и шестая


Гном 2. Возвращение.

Глава первая

Глава вторая и третья

Глава четвертая и пятая

( Читать дальше )

Как обогнать индекс (пример выигрышной торговой стратегии)

          В кругу экономистов бытует мнение, что обогнать фондовый индекс на длительной перспективе невозможно, и если вам удалось в какой-то определенный год вырваться вперед, получив прибыль гораздо выше той, которую продемонстрировал индекс акций, то в будущем неизбежно ваши результаты не превзойдут индекс, а могут оказаться только хуже него. Подобная точка зрения следует из гипотезы эффективного рынка. К сожалению, экономика отличается от математики тем, что строгое доказательство практически любого утверждения представляется невозможной задачей. Тем не менее, в данной статье мне бы хотелось привести пример одной из стратегий, которая способна обогнать индекс акций в длительной перспективе. Разумеется, я отдаю себе отчет в том, что не могу доказать это математически. Впрочем, в экономике практически везде используются различные гипотезы, которые невозможно доказать, например, почему-то принято  считать, что движение цен подчиняется нормальному распределению, и я что-то нигде не встречал какого-либо доказательства подобного утверждения. Тем не менее, именно на основе гипотезы о нормальном распределении была придумана знаменитая формула Блэка-Шоулза для оценки стоимости опционов, за которую ее авторы даже получили нобелевскую премию.

( Читать дальше )