SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
коэффициент альфа
К вопросу об Альфе
- 31 мая 2016, 14:12
- |
Классический расчет α управления осуществляется через линейную регрессию:
ΔSt=βΔBt+α+εt,
где ΔSt — приращение счета в %, «очищенное» от вводов-выводов (для фондов — приращение стоимости «пая» или акций фонда),
ΔBt — приращение бенчмарка в %,
εt — ошибка линейной регрессии.
Как видите, «лучше бенчмарка» на росте или на падении ничего не говорит нам о знаке α. Потому что быть лучше бенчмарка на росте можно за счет β>1 даже с отрицательной альфой, а на падении — за счет β<1. И только одновременный «обыгрыш» бенчмарка и на росте и на падении приведет к тому, что α, рассчитанная по всему периоду будет положительна. Более того, α может быть положительна и при проигрыше бенчмарку на росте и только при проигрыше бенчмарку на падении она с большой вероятностью будет отрицательна.
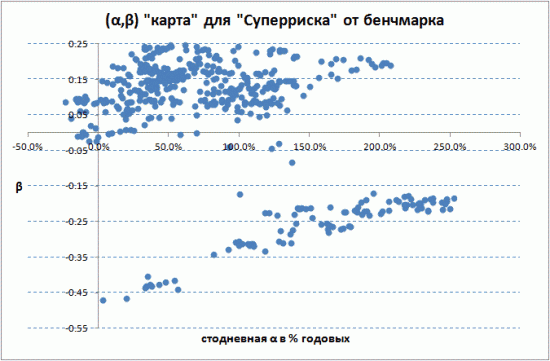
Но все, кто хоть раз считал α и β, прекрасно знают, что они нестационарны по времени и их значения, вычисляемые, например, по 100 тактам, временами сильно отличаются от результатов расчетов на всей истории. Но это хоть можно наглядно отследить, построив «альфа-бета карту» относительно бенчмарка. Вот, например, 100-дневная «альфа-бета карта» для нашего расчетного портфеля, ранее называвшегося «Суперриск»:
относительно бенчмарка, определенного здесь (аналог рублевого buy&hold на фьючерсе, только рассчитываемый по значениям самого индекса)
( Читать дальше )
ΔSt=βΔBt+α+εt,
где ΔSt — приращение счета в %, «очищенное» от вводов-выводов (для фондов — приращение стоимости «пая» или акций фонда),
ΔBt — приращение бенчмарка в %,
εt — ошибка линейной регрессии.
Как видите, «лучше бенчмарка» на росте или на падении ничего не говорит нам о знаке α. Потому что быть лучше бенчмарка на росте можно за счет β>1 даже с отрицательной альфой, а на падении — за счет β<1. И только одновременный «обыгрыш» бенчмарка и на росте и на падении приведет к тому, что α, рассчитанная по всему периоду будет положительна. Более того, α может быть положительна и при проигрыше бенчмарку на росте и только при проигрыше бенчмарку на падении она с большой вероятностью будет отрицательна.
Но все, кто хоть раз считал α и β, прекрасно знают, что они нестационарны по времени и их значения, вычисляемые, например, по 100 тактам, временами сильно отличаются от результатов расчетов на всей истории. Но это хоть можно наглядно отследить, построив «альфа-бета карту» относительно бенчмарка. Вот, например, 100-дневная «альфа-бета карта» для нашего расчетного портфеля, ранее называвшегося «Суперриск»:

относительно бенчмарка, определенного здесь (аналог рублевого buy&hold на фьючерсе, только рассчитываемый по значениям самого индекса)

( Читать дальше )
- комментировать
- ★28
- Комментарии ( 80 )
Коэф Шарпа, Трейнора и прочее, нужно разобраться?
- 04 марта 2014, 16:17
- |
Добрый день, коллеги!
Помогите разобраться:
Решил проанализировать свою систему торговли с «умной» стороны, т. е. при помощи различных коэф Шарпа, Трейнора, Бета, альфа и прочее, вот что получилось:
Вводные данные:
Доходность ММВБ за 2013 год: 3.27%
Безрисковый актив: 10% (банковская ставка)
Доходность портфеля: 40.59%
Стандартное отклонение: 3.57%
На выходе:
коэф. Шарпа: 8.56
коэф. Бета: 0.04
коэф. Трейнора: 8.2
коэф. Альфа Дженсена: 30.84%
ВНИМАНИЕ ВОПРОС: Это хорошие показатели, плохие или средние? Или я, что-то не правильно посчитал?
За ранее всем спаибо за ответы!
P. S. Нашел ошибку в расчетах, спасибо тем кто мне на нее указали. Не верно было посчитано стандартное отклонение.
Стандартное отклонение: 27% и соответсвенно коэф. Шарпа: 1.13
Спасибо всем кто помог!
Помогите разобраться:
Решил проанализировать свою систему торговли с «умной» стороны, т. е. при помощи различных коэф Шарпа, Трейнора, Бета, альфа и прочее, вот что получилось:
Вводные данные:
Доходность ММВБ за 2013 год: 3.27%
Безрисковый актив: 10% (банковская ставка)
Доходность портфеля: 40.59%
Стандартное отклонение: 3.57%
На выходе:
коэф. Шарпа: 8.56
коэф. Бета: 0.04
коэф. Трейнора: 8.2
коэф. Альфа Дженсена: 30.84%
ВНИМАНИЕ ВОПРОС: Это хорошие показатели, плохие или средние? Или я, что-то не правильно посчитал?
За ранее всем спаибо за ответы!
P. S. Нашел ошибку в расчетах, спасибо тем кто мне на нее указали. Не верно было посчитано стандартное отклонение.
Стандартное отклонение: 27% и соответсвенно коэф. Шарпа: 1.13
Спасибо всем кто помог!
Хедж-фонд стартап в России. Делюсь открытиями + как устроен инвестбизнес
- 05 марта 2013, 13:56
- |
Итак, два месяца плюс минус я вникал в тему создания хедж-фонда. Хочу поделиться интересными открытиями, к которым я пришел.
Если вы создали фонд, то вы бьетесь с операционными костами и пытаетесь ужать их в плату за управление 2% от активов, и думаете как заработать свои 20% от положительного перформанса.
Проблем тут масса:
Рассмотрим другой, альтернативный, чисто российский вариант. Если вы похитрее, вы делаете УКашечку. И ведете раздельные счета. У вас 4 трейдера, у которых к тому же может быть по три стратегии, на каждого вы вещаете инвесторов.
( Читать дальше )
- Запустить фонд, который будет успешен долгие годы — архисложная задача.
- На этапе запуска фонда реальное значение имеет везение.
- В России нет хедж-фондов, которые ведут открытый перформанс и показывают свою способность делать альфу.
- Те кто на самом деле умеет делать деньги, сидят тихо и никто о них не знает.
Если вы создали фонд, то вы бьетесь с операционными костами и пытаетесь ужать их в плату за управление 2% от активов, и думаете как заработать свои 20% от положительного перформанса.
Проблем тут масса:
- Надо во что бы то ни стало заработать в первый год, иначе косты сожрут все, а инвесторы выведут деньги.
- Кто-то должен заниматься инвестициями, кто-то должен вести бизнес фонда — нужны партнеры.
- Где взять хороших трейдеров? Даже те звезды которые считают себя хорошими трейдерами, которые работали на деске и зарабатывали большие деньги, когда фронтраннили крупных клиентов или же почувствовали себя гениями на волне мегаралли на разивающихся рынках 2000-х годов, могут стоить очень дорого, и иметь нулевое КПД.
- В любом случае, чтобы заинтересовать высококлассных трейдеров, придется делать их партнерами фонда, чтобы они не убежали в другой фонд.
- Тут встает еще одна проблема — допустим у тебя
- 1 фонд, 4 трейдера.
- Что делать, если 3 трейдера слились, а 1 заработал? если фонд ушел в минус, то даже тот трейдер который заработал не получит свой перформанс бонус.
- Вообще говоря модель 1 фонда, когда твои доходы строго зависят от абсолютного дохода единого фонда — недиверсифицированна и крайне рискованна с точки зрения бизнес-плана и инвестиций в такой проект. Но, с точки зрения отношения к инвесторам такая модель является наиболее честной. Потому что все максимально прозрачно. И если управляющий показывает доходность по фонду, то он действительно зарабатывает деньги и тут не может быть никаких НО.
Рассмотрим другой, альтернативный, чисто российский вариант. Если вы похитрее, вы делаете УКашечку. И ведете раздельные счета. У вас 4 трейдера, у которых к тому же может быть по три стратегии, на каждого вы вещаете инвесторов.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал
