SMART-LAB
Новый дизайн
Мы делаем деньги на бирже
опционы
Здесь вы найдете самую полную в российском интернете коллекцию актуальных записей по торговле опционными контрактами, опционных стратегиях, вопросах по опционам.
Портфель разумного инвестора. Концепция долгосрочных инвестиций. Часть 3
- 03 ноября 2012, 15:41
- |
Начало тут
http://smart-lab.ru/blog/ideas/85545.php
http://smart-lab.ru/blog/ideas/85547.php
СИСТЕМА А.
Суммируя всю информацию — получаем следующий алгоритм:
( Читать дальше )
http://smart-lab.ru/blog/ideas/85545.php
http://smart-lab.ru/blog/ideas/85547.php
СИСТЕМА А.
Суммируя всю информацию — получаем следующий алгоритм:
- Производим отбор и составляем список акций пригодных для инвестиций, определяем «справедливую» стоимость, покупки возможны при «запасе прочности» равным 2 = стоимость/цена. Это самая сложная часть, но от нее будет зависеть – Ваш портфель будет лучше рынка или хуже. Пример Баффетта показывает, что «правильный» выбор компаний может значительно улучшить Ваши результаты в сравнении с рынком, и даже без использования «попутного ветра».
- Раз в месяц определяем «Индекс А». Если он ниже 85, то ждем. Ежемесячные сбережения направляем в депозиты. Кстати, вопрос СБЕРЕЖЕНИЙ очень важен, в этой статье никак не затронут. Но я факт сбережений опустил по умолчанию, так как, если Вам не оставили большого наследства, то сбережения делать нужно. Без сбережений нельзя будет делать инвестиции.
( Читать дальше )
- комментировать
- ★33
- Комментарии ( 0 )
Портфель разумного инвестора. Концепция долгосрочных инвестиций. Часть 2
- 03 ноября 2012, 15:38
- |
ЧТО ПОКУПАТЬ?
Выбор акций производится по методике определения справедливой стоимости (фундаментальный анализ) основанной на трудах Уоррена Баффетта и Бенджамена Грэхема (их книги «Эссе …» и «Разумный инвестор»).
Основные критерии при отборе компаний для начала оценки компаний:
— Лидерские позиции в своей отрасли, граничащие с монополизмом («незаменимый продукт»);
— Наличие широко известного бренда;
— Отличное руководство;
— Поступательное развитие компании – рост выручки, чистой прибыли и собственного капитала за последние 5 лет (отсутствие убытков);
— Капитализация компании не менее 200 млн. долл.
( Читать дальше )
Выпустят ли парня кто натарил 155 колов до экспиры?
- 01 ноября 2012, 17:49
- |
Выпустят ли парня кто натарил 155 колов до экспиры?
Trade idea: Sell WMB dec strangle P33 (1.025), C36(0.97), delta hedged (364 stocks)
- 31 октября 2012, 19:53
- |
Март-стратегический взгляд на маркет
- 31 октября 2012, 18:36
- |
безотносительно новостей и информации, за исключением ценовой:
аптренда больше нет
очень, вероятно, стоим в начале даунтренда
волатильность по индексу минимальная
сдается мне, волатильность сильно недооценена
волатильность сейчас в 2 раза ниже, чем 1 года назад
(использовал график индекса волатильности — вопрос опционщикам — а какая волатильность на самом деле??? И где ее посмотреть)
рынок наш подливают аккуратно, без шума и пыли

сдается мне мы близко от области, в которой плавное сползание может превратиться в довольно быстрый нырок со 140 на 130 (1-2 дня).

Такова сейчас рабочая гипотеза по рынку.
p.s. удобные графики на смартлабе: http://smart-lab.ru/g/
аптренда больше нет
очень, вероятно, стоим в начале даунтренда
волатильность по индексу минимальная
сдается мне, волатильность сильно недооценена
волатильность сейчас в 2 раза ниже, чем 1 года назад
(использовал график индекса волатильности — вопрос опционщикам — а какая волатильность на самом деле??? И где ее посмотреть)
рынок наш подливают аккуратно, без шума и пыли

сдается мне мы близко от области, в которой плавное сползание может превратиться в довольно быстрый нырок со 140 на 130 (1-2 дня).

Такова сейчас рабочая гипотеза по рынку.
p.s. удобные графики на смартлабе: http://smart-lab.ru/g/
Далекое эхо Margin
- 31 октября 2012, 17:41
- |
Обрастя некоторым количеством знаний, пытаюсь воспроизвести идеи известных тредеров (да простит меня margin:))
Итого, скринером ищем сегодняшние квартальные отчеты по американским стокам, имеющие заметную капиталлизацию.
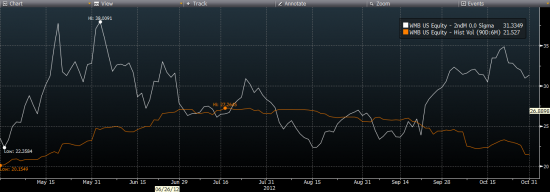
По истории каждого инструмента выбираем те у которых наиболее распространен гэп на квартальных отчетах. По какойто причине мне больше всех понравился BMC(производитель ПО)
Смотрим график
( Читать дальше )
Итого, скринером ищем сегодняшние квартальные отчеты по американским стокам, имеющие заметную капиталлизацию.

По истории каждого инструмента выбираем те у которых наиболее распространен гэп на квартальных отчетах. По какойто причине мне больше всех понравился BMC(производитель ПО)
Смотрим график
( Читать дальше )
Опционы: легко и просто или ловушка?
- 31 октября 2012, 15:17
- |
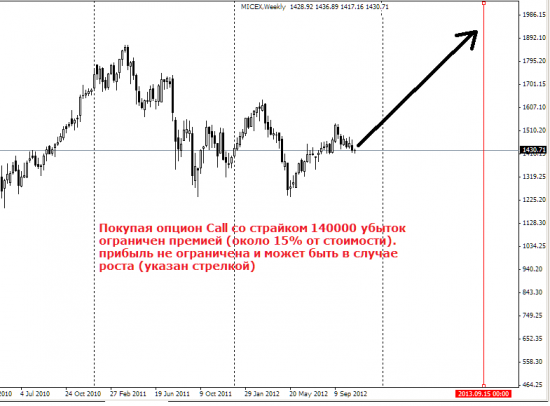
Сейчас на фортс есть опционы на фьючерс ММВБ MIX-9.13M160913CA xxxxx со сроком экспирации 16.09.2013. Допустим, что Сегодня фьючерс на ммвб MXU3 торгуется по 139800 (т.е. со скидкой к индексу). Я пишу допустим, потому что в стакане нет маркетмейкера.
Получается, что я сейчас могу купить call и put опционы со страйком 140000 и держать их до 16.09.2013.
Если цена фьючерса MXU3 (MIX 9.2013) вырастет, например, 1 февраля 2013 до 160000, то я могу потребовать исполнить опционы по цене 140000.
( Читать дальше )
Получается, что я сейчас могу купить call и put опционы со страйком 140000 и держать их до 16.09.2013.
Если цена фьючерса MXU3 (MIX 9.2013) вырастет, например, 1 февраля 2013 до 160000, то я могу потребовать исполнить опционы по цене 140000.

( Читать дальше )
Что ждет позиции по уже открытым контрактам на индекс в процессе его замены?
- 31 октября 2012, 13:19
- |
— Проезжая через станцию и будучи голоден в рассуждении чего бы покушать я не мог найти постной пищи. Дьякон Духов.
— Лопай, что дают.
А.П.Чехов, Жалобная книга
В связи с началом расчета индексов Московской биржи 18.12.2012, о которой я писал ранее здесь, по новой методике произойдет, по сути, замена базисного актива по уже открытым позициям в срочных контрактах со сроками H3 (март 2013) и далее. Согласитесь, выглядит забавным, когда вы открыли позиции исходя из действующей спецификации, а затем она была изменена, и ваш фьючерс или опцион стал производной от цены уже совсем иного базисного актива. Предусмотрены ли такие изменения и каков порядок переноса старых позиций?
Ответ весьма прост и угадывается в действующих спецификациях, например п. 8.4 спецификации фьючерсного контракта на индекс РТС:
8.4. С момента вступления в силу изменений и дополнений в настоящую спецификацию условия существующих обязательств по ранее заключенным Контрактам считаются измененными с учетом таких изменений и дополнений.
Мило, не правда ли? Мы заменили базисный актив (по сути обязательства биржи по его расчету), но вы не волнуйтесь, все ваши обязательства остаются в силе. Одностороннее изменение условий договора или только у меня «кипит наш разум возмущенный»?
— Лопай, что дают.
А.П.Чехов, Жалобная книга
В связи с началом расчета индексов Московской биржи 18.12.2012, о которой я писал ранее здесь, по новой методике произойдет, по сути, замена базисного актива по уже открытым позициям в срочных контрактах со сроками H3 (март 2013) и далее. Согласитесь, выглядит забавным, когда вы открыли позиции исходя из действующей спецификации, а затем она была изменена, и ваш фьючерс или опцион стал производной от цены уже совсем иного базисного актива. Предусмотрены ли такие изменения и каков порядок переноса старых позиций?
Ответ весьма прост и угадывается в действующих спецификациях, например п. 8.4 спецификации фьючерсного контракта на индекс РТС:
8.4. С момента вступления в силу изменений и дополнений в настоящую спецификацию условия существующих обязательств по ранее заключенным Контрактам считаются измененными с учетом таких изменений и дополнений.
Мило, не правда ли? Мы заменили базисный актив (по сути обязательства биржи по его расчету), но вы не волнуйтесь, все ваши обязательства остаются в силе. Одностороннее изменение условий договора или только у меня «кипит наш разум возмущенный»?
крупные покупки 155-ых ноябрьских колов
- 30 октября 2012, 18:53
- |
Если ничего не путаю, то прошли крупные покупки 155-ых колов с ноябрьской экспирацией.
Волатильность конкретно на этом страйке сильно задрали вверх. Открытые позиции по этому страйку тоже сильно вырасли.
К чему бы это?)
Помогите вниз опустить волу… предлагаю продать его и купить 145-150-ые).
Волатильность конкретно на этом страйке сильно задрали вверх. Открытые позиции по этому страйку тоже сильно вырасли.
К чему бы это?)
Помогите вниз опустить волу… предлагаю продать его и купить 145-150-ые).
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал