Блог им. Gusan |Почему не могут? Могут!
- 16 мая 2020, 01:33
- |
Тут неожиданно призвали к ответу: почему дескать опционный софт написал, а заработать сам не можешь?
Наезд странный: программить это одно, а трейдить этож совсем другое. И знания совсем другие, и психология. Если программист может уйти в астрал и долго там витать, то трейдер должен быть шустрым-быстрым и всегда на чеку. Схватил добычу и быстро в кусты. Не жадничать, а то очень быстро из охотника сам в жертву превратишься. Не быть инертным, быстро признавать ошибку и готовность перевернуться в противоположное направление. Программист же более инертен и упрям. Грубо говоря: программист — интраверт, трейдер — экстраверт.
В общем, торговля и программинг вещи сильно разные. Но лично мне удалось немного заработать. Вот здесь описал свой опыт торговли в 2018г. Там 09.04.2018 за день удалось утроить депо. Но это просто повезло в хорошей позе оказаться перед гэпом. Тем более потом часть слил и закрыл торговлю в реале. Стал снова теорию копать и программить. Но ушел все-таки в плюсе: было 100тр, стало 383тр.
( Читать дальше )
- комментировать
- ★11
- Комментарии ( 67 )
Блог им. Gusan |Вега и Вомма
- 15 марта 2020, 03:27
- |
Возможно, не все знают про нелинейные эффекты грека Веги и волшебные свойства грека Воммы. По нынешним волатильным временам, когда вола ходит туда-сюда на десятки процентов — эти эффекты могут значительно повлиять на финрез при торговле волатильностью. Хочу поделиться своим видением — может кому будет интересно. А может кого убережет от опасной позиции с неоправданным риском.
Итак, рассмотрим проданный стрэдл:
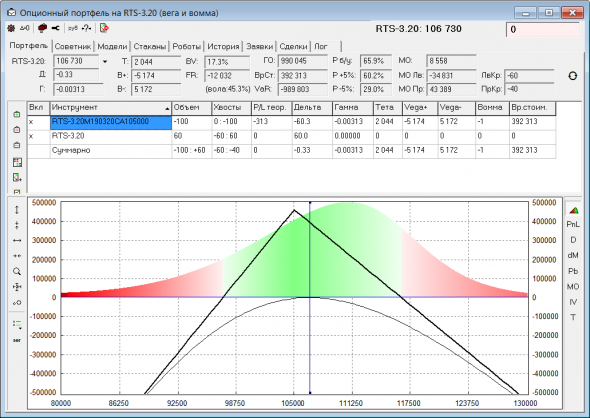
Это обычный профиль PnL, который рисуют все опционные программы. Фактически, это зависимость PnL позиции от первого момента (M1) распределения вероятностей, где окажется цена БА на экспирацию (вон оно на заднем фоне профиля). M1 = текущей цене БА. Т.е. мысленно двигаем все распределение влево-вправо (меняем M1) и считаем, как изменится PnL позиции при этом. Но, когда торгуем волатильностью, влияние первого момента ведь стараемся исключать используя дельтахедж (ДХ). И в большей степени нас должен интересовать профиль PnL от второго момента распределения (M2). Именно от него зависит финрез торговли волатильностью. Фактически, M2 почти тоже самое, что IV на центре улыбки (IVC). Смотрел на истории, специальным образом нормированный M2 (на цену БА и время до экспы) коррелирует с IVC почти 100%.
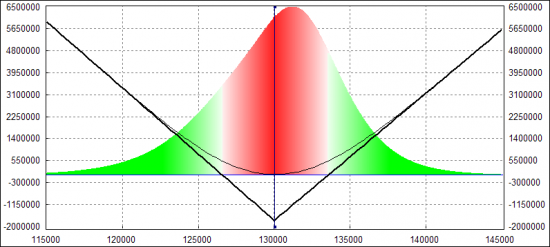
Если у нас есть опционная модель, в которой можно точечно менять второй момент, то легко посмотреть профиль PnL от изменений M2. Я использую замечательную модель Курбаковского, в которой главный параметр mI — как раз и отвечает за второй момент. Поэтому добавил в своей программе отрисовку такого профиля. И вот что рисует для проданного стрэдла:
( Читать дальше )
Блог им. Gusan |Модель Курбаковского, сглаживание и нормировка
- 14 декабря 2019, 13:03
- |
Большое спасибо Виталию Курбаковскому, что опубликовал свою обобщенную модель ценообразования опционов (1, 2, 3, 4, 5). Давно хотелось подобную модель, с минимум параметров, физический смысл которых был бы более-менее понятен. Чтобы можно было осознано свои параметры модели задавать, а не подгоняться под рынок и слепо за ним идти. Модель, которую использует биржа (с шестью параметрами ABCDES) под такой запрос не подходит. Попробуй там пойми, все ли шесть параметров сейчас имеют справедливые и оправданные значения, или с каким-то из параметров можно поспорить. И слишком уж она гибкая. Бывало смотришь — выскочила какая-то котировка за модель, только соберешься по ней ударить, а программа параметры модели подкорректировала и услужливо изогнула кривую с учетом новой котировки. И то, что только что
выбивалось за модель, стало ей соответствовать. Пробовал еще модель китайской улыбки, там и параметров поменьше и смысл у них попонятнее, но очень уж плохо она подгоняется под рынок. И тут, на счастье, Виталий поделился своей моделью и все подробно объяснил. Реализовал у себя и оказалось — то что надо. И в рынок хорошо вписывается, и параметры имеет понятные.
( Читать дальше )
Блог им. Gusan |Дельта-нейтральность через матожидание
- 04 февраля 2018, 22:35
- |
Возникла тут одна идея — как можно было бы добиваться дельта-нейтральности опционной позиции. Хотел бы поделиться, может, получится интересное обсуждение. Но сначала — предыстория вопроса.
Итак, допустим, мы торгуем какую-то дельта-нейтральную стратегию. Это может быть и покупка-продажа волатильности, и котирование ММ, и календарный арбитраж между разными сериями или еще какая. Главное, после открытия опционной позиции (по выгодным, как нам кажется, ценам), нужно добавить фьючерсов в позу (лонг или шорт), чтобы минимально зависеть от того, куда пойдет базовый актив (БА). Как это сделать? Самое простое — посчитать дельту по Блеку-Шоулзу (БШ) и выровнять эту дельту соответствующим количеством фьючерсов. Рассмотрим на примере покупки волатильности:
Здесь дельта БШ равна нулю и, по идее, нам все равно, куда пойдет БА. Правда будет сильная зависимость от веги, но этот риск здесь рассматривать не будем, только риск от движения БА. Судя по картинке и по тому, что дельта БШ = 0 — у нас нет такого риска. Но если мы в реале откроем эту позу, то обнаружим, что есть почти 100% корреляция эквити с БА. Если она положительная (растет БА — растет PnL, падает БА — падает PnL), то, значит, у позы фактически положительная дельта. Если корреляция отрицательная (растет БА — падает PnL, и наоборот), то фактически у нас отрицательная дельта. Несмотря на то, что БШ показывает нам нулевую дельту. Перефразируя известное выражение, можно было бы сказать так:
( Читать дальше )
Блог им. Gusan |Эмпирическое распределение
- 10 января 2017, 23:01
- |
Интересную тему с эмпирическими распределениям подняли Дмитрий Новиков и Nonsense. Хотелось бы одну мысль по этому поводу озвучить. Насколько понимаю, эмпирическое распределение — это когда берут историю цен БА, нарезают неким окном, из каждого полученного отрезка получают приращение, и потом строят частотную диаграмму из этих приращений. Полученное распределение и называют эмпирическим. Nonsense пишет, что возникают две проблемы:
1. У полученного распределения мю может быть не ноль, и если считать по этому распределению справедливые цены, то не будет выполняться колл-пут паритет.
2. Выбор размера окна для нарезки.
Мне же кажется, что тут другая, более существенная, проблема. Предположим, у нас есть некий случайный процесс, с помощью которого мы можем сгенерировать кучу случайных траекторий цены:
( Читать дальше )
Блог им. Gusan |Распознать тренд
- 07 декабря 2015, 16:13
- |
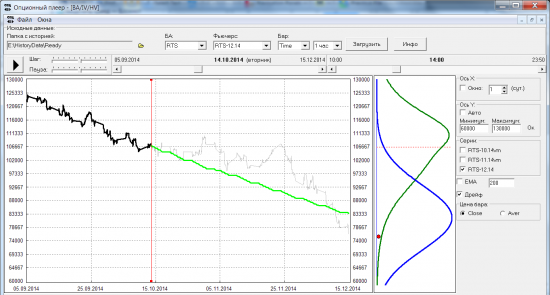
Справа два графика плотности распределения за два месяца до экспирации: синяя линия у распределения по модели с трендом, зеленая — рыночное распределение (из текущей в тот момент улыбки IV). Красный шарик — это где реально произошла экспирация. Видно, что модельное распределение спрогнозировало цену экспирации точнее, чем рыночное. Используя такую модель на этом квартале, можно было бы открыть опционную позу с очень большой ожидаемой доходностью.
Но такая идиллическая картинка, конечно, далеко не на всех кварталах. Чаще вот такая ситуация:
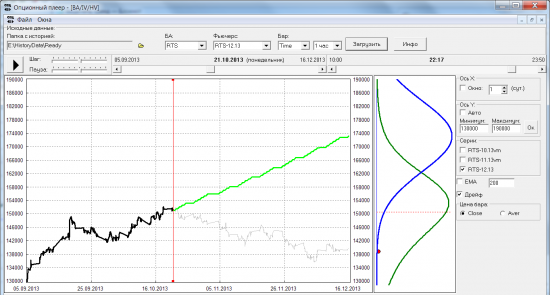
( Читать дальше )
Блог им. Gusan |Рынок vs модель
- 27 октября 2015, 00:56
- |
Для начала рассмотрим рыночное распределение вероятности (сразу обозначим его как Q). Получать его будем из биржевой улыбки волатильности. Как это делать -рассказывал и Андрей Агапов, и Владимир Твардовский в этом видео. Поскольку это распределение соответствует рыночным ценам, можно считать, что распределение Q — это усредненный прогноз рынка на экспирацию. Имея потиковую историю улыбок волатильности, можно построить потиковую историю распределения вероятности; и зная цену экспирации — можно вычислить в любой момент времени, с какой точностью рынок (распределение Q) угадывал, где произойдет экспирация. Рассмотрим, например, историю RTS-6.14:
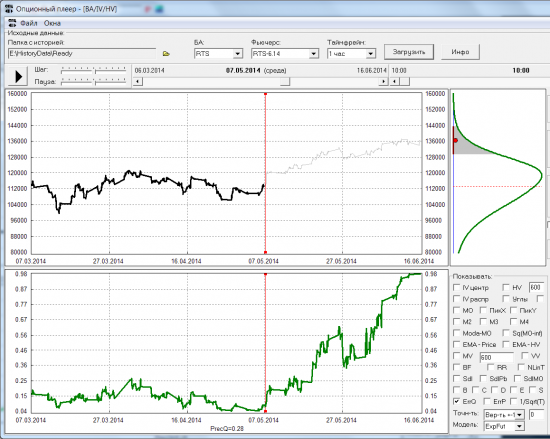
( Читать дальше )
Блог им. Gusan |Справедливая стоимость опциона
- 11 октября 2015, 15:38
- |
Хотелось бы порассуждать на тему справедливой стоимости: что это такое, есть ли в ней практический смысл, и т.д. Все рассуждения — с точки зрения долгосрочной торговли опционами внутри одной календарной серии: когда есть некий прогноз на экспирацию, открывается поза, и с редким управлением (или даже без) она доводится до экспирации.
Итак, если не ошибаюсь, справедливая стоимость опциона определяется как ожидаемый доход от опциона. Здесь и далее предлагаю считать, что затраты на поддержание позиции = 0, комиссию и спред не учитываем. Рассмотрим сначала упрощенный пример (взял из книги «Опционы» Натенберга): пусть цена БА сейчас 100п, а на экспирацию возможны только пять значений: 80, 90, 100, 110, 120 и вероятность каждого исхода = 20%. Посчитаем справедливую стоимость опциона 100 Колл. Если БА на экспу будет равен 80, 90 или 100, то такой колл ничего не даст. Если БА будет 110п, то доход будет 10п. Если 120п, то доход 20п. Ожидаемый доход от такого опциона (предположим, что он достался нам бесплатно) будет:
( Читать дальше )
Блог им. Gusan |Распределение ОИ
- 10 августа 2015, 02:59
- |
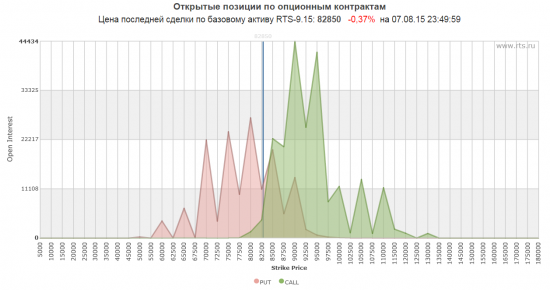
Эта картинка напоминает колокол плотности распределения. Но смущает, что тут много пиков (на страйках с шагом 5000п) и провалов (на страйках с шагом 2500п). Что вряд-ли соответствует действительному распределению вероятностей. Поэтому захотелось как-то сгладить эти пики и провалы. Решил сделать так: идем слева направо, и накапливаем ОИ путов и коллов. Получается такая картинка:
( Читать дальше )
Блог им. Gusan |Точность прогноза
- 27 июня 2015, 01:17
- |
Допустим, есть две системы, которые выдают прогноз — где будет БА на экспирацию. Прогноз выдается в виде распределения вероятностей. Задача: оценить на истории — какая система выдает более точный прогноз.
Вот картинка для иллюстрации. Слева график цены БА, справа два графика плотности вероятности, синий для распределения P, зеленый для распределения Q. Красным кружочком отмечен уровень S, где реально оказалась прогнозируемая цена:
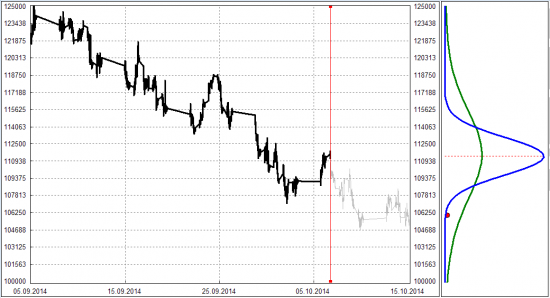
Для оценки точности прогноза пробовал считать средний квадрат отклонения распределения от S (кажется, этот метод называется MSE). Для вышеприведенной картинки такое отклонение меньше у распределения P. Но, мне кажется, что распределение Q более точное: оно дает гораздо большую вероятность для красного кружочка.
Может кто подскажет — можно ли как-то по другому считать точность распределения-прогноза?
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс



















