Блог им. uralpro |Определение факторов прибыльности стратегии
- 21 февраля 2016, 11:48
- |
Статья из блога www.jonathankinlay.com поможет лучше понять работу вашей торговой стратегии и повысить ее производительность в будущем.
Построение прибыльной стратегии только половина успеха, трейдеру еще необходимо понимание так называемой альфы стратегии и риска. Это значит, что нужно определить факторы, обуславливающие прибыльность алгоритма и, в идеале, создать модель так, что их относительный вклад может быть вычислен. Более продвинутый путь — это конструирование мета-модели, которая будет предсказывать прибыльность и давать рекомендации, каким образом должна торговать стратегия в следующий период.
Производительность стратегии
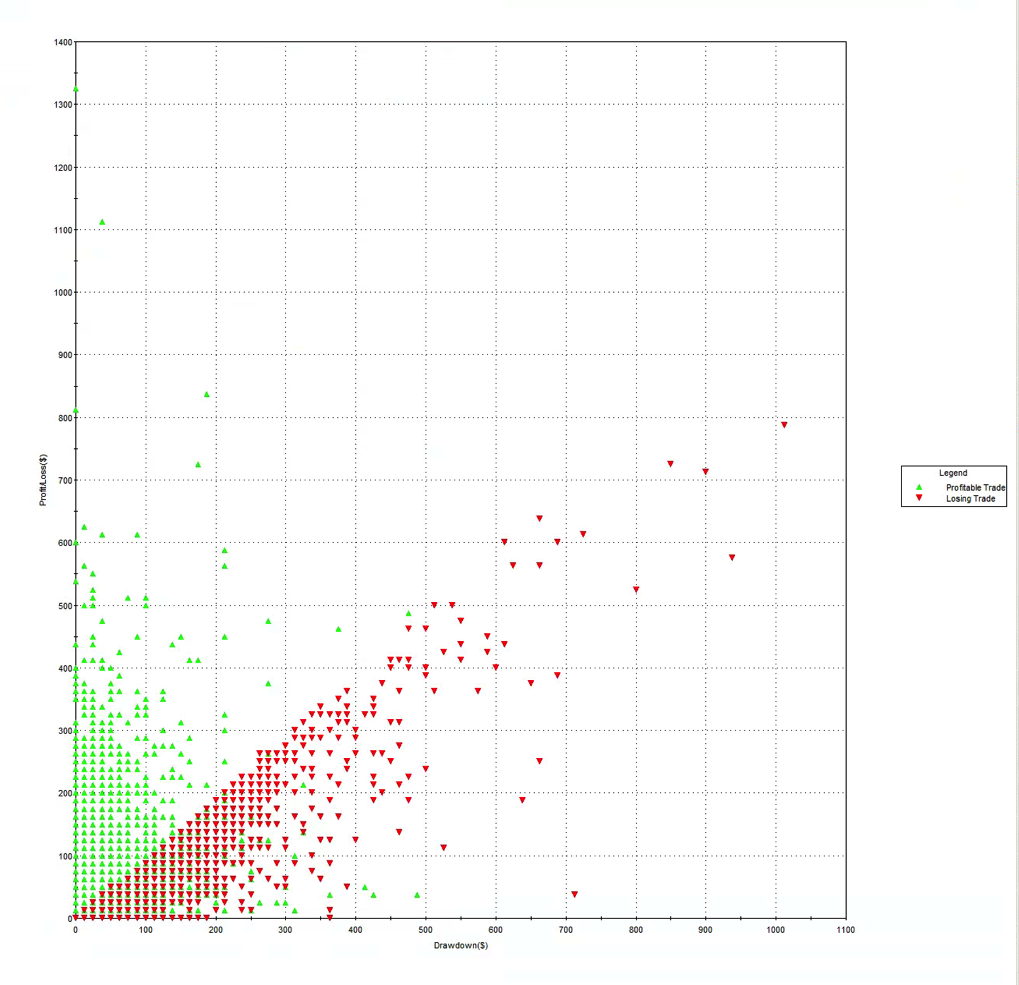
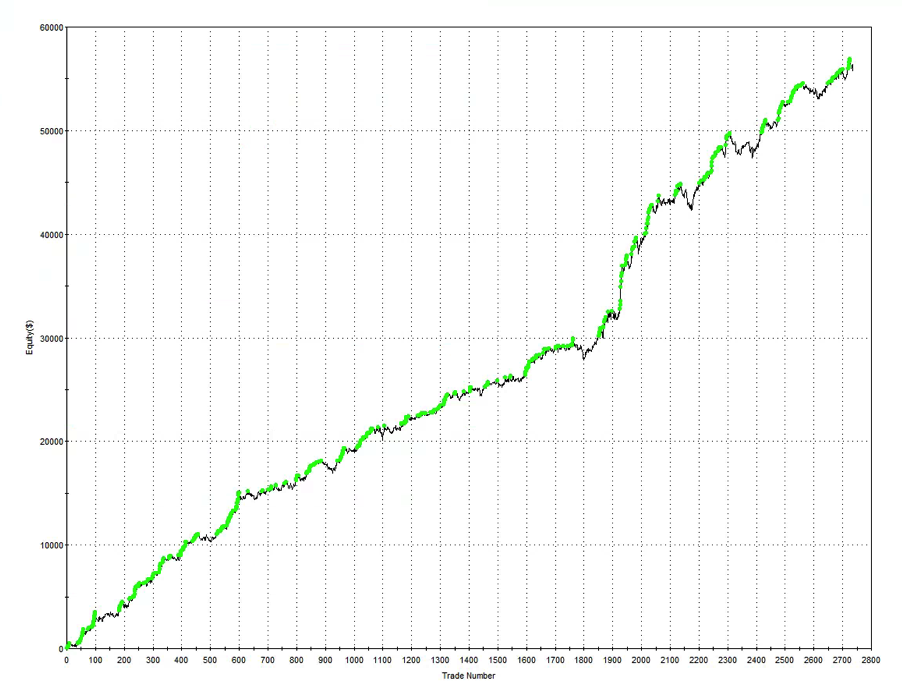
Давайте посмотрим, как это работает на практике. В нашем случае будем использовать следующую внутридневную стратегию на фьючерсах E-mini:
Общая производительность стратегии довольна высока. Среднемесячная прибыль за период с апреля по октябрь 2015 года почти 8 000 долларов на контракт, за вычетом комиссии, со стандартным отклонением всего 5 500 долларов. Годовой коэффициент Шарпа около 5.0. На платформе с хорошим исполнением стратегия может масштабироваться до 10-15 контрактов, с годовой прибылью от 1 до 1.5 миллионов долларов.
( Читать дальше )
- комментировать
- ★27
- Комментарии ( 6 )
Блог им. uralpro |Линейная регрессия с использованием фильтра Калмана
- 23 апреля 2015, 10:12
- |
Линейная регрессия часто используется для вычисления пропорции хеджирования в парном трейдинге. В идеальной ситуации коэффициенты этой регрессии — наклон линии регрессии и свободный член (пересечение) остаются всегда постоянными. Однако в реальности все, конечно, не так радужно, и значения этих параметров постоянно меняются во времени. Как правильно вычислять коэффициенты регрессии, чтобы избежать подгонки к текущей ситуации, рассматривается в статье "Online Linear Regression using a Kalman Filter". Для этой цели в данной публикации используется фильтр Калмана.
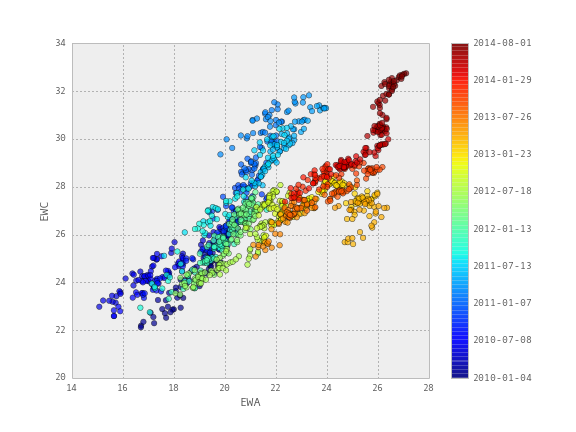
Для тестирования берутся исторические цены закрытия двух биржевых фондов ETF — австралийского EWA и канадского EWC с 2010 по 2014 год. Динамика цен этих фондов показывает взаимосвязь, что продемонстрировано на диаграмме рассеивания в заглавии поста. Однако по этому же графику видно, что эту взаимосвязь невозможно описать с помощью линейной регрессии с постоянными коэффициентами.
( Читать дальше )
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- си
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс