Что такое гомочартизм в трейдинге и кто такой трейдер-гомочартист
 (Гомо  —  единственный, однородный,  chart – график).
Гомочартизм – направление в трейдинге, состоящее в том, что анализируются параметры исключительно одного выбранного  инструмента с глубочайшей верой  и мистической уверенностью  в то,  что этого достаточно для прогноза  его движения. Поэтому приверженцев такого направления можно определить  как секту, члены которой поклоняются учениям любимых  руководителей гуру  и классиков теханализа, написавших книги в 20-80-х годах прошлого столетия.   
Гомочартист – трейдер-сектант, исповедающий гомочартизм, обычная фраза  при  больших просадках эквити, порой уходящих в отрицательную зону: «видите ли, господа, рынок изменился». Его мечта (несбыточная) подобрать так параметры  торговой системы, чтобы  эквити было в плюсе для любых рынков и во все времена, игнорируя текущее состояние среды обитания этого инструмента. Логика его  проста и всегда правильно отвечает на риторический вопрос: разве могут все зеленые мухи ошибаться?


( Читать дальше )

Привет. 

Вопрос к практикующим алго-трейдерам. (Новичкам данный пост просто необходим — выношу грааль на общее обозрение)

Есть система N с четырьмя оптимизируемыми параметрами.

Выбирая 500 лучших результатов по некоторому соотношению (какому? читай мои посты ранее) я получаю распределения параметров в каждом из 500 наблюдений (то есть значение «1» параметра 1 наблюдалось 0 раз, значение «2» параметра 1 наблюдалось 49 раз, значение «3» параметра 1 наблюдалось 110 раз и т.д.):



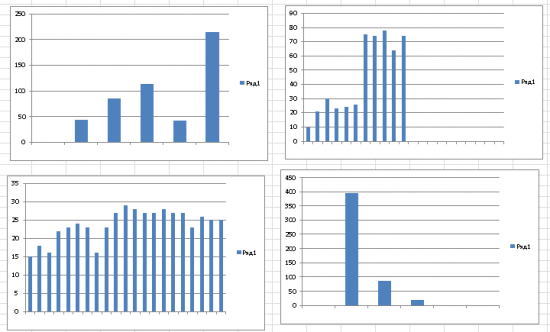
Правильно ли я понимаю, что третий рисунок говорит нам о том, что параметр 3 слабо влияет на итоговый результат системы и что оптимизировать его нет смысла.

Update: параметр x выпал y раз 

Привет

Всегда торгуя опционами мы несём на себе несколько экзотических рисков, которые не учтены в стандартном наборе греков(дельта, гамма, вега, тета, ро). Такие как: 
-риск уменьшения/увеличения skew(vanna). Этот параметр в стохастических моделях учитывает корелляцию базвого актива и волатильности. 
-риск уменьшения/увеличения curve улыбки(насколько улыбка сильно «улыбается»)(volga)
-риск горизонтального(параллельно) сдвига улыбки(особенно важен тем кто активно торгует под экспирацию). Выводится через модифицированную дельту. К блэковской дельте(dBs/dS) добавляется (DBs/dsigma(vol))*(dsigma(param)/dS).

Подобрать все эти параметры очень удобно и не сложно через модель sabr. Матлаб в помощь. 

Если использовать эти параметры в торговле опционами хедж будет более аккуратным. Если кто торгует просто спреды, то тому наверно всё это до лампочки и это правильно. Но если кто-то использует более сложные вещи(маркет-мейкинг к примеру), то тому данная вещь будет наверняка интересна.

 

                  В околоопционном  информационном  пространстве широко представлены описания классических опционных стратегий. Но стратегия, описанная ниже упоминается редко или вообще не упоминается, хотя в последнее время вызывает всё больше интереса и споров.  Когда-то решил тезисно набросать  мысли по ней – сейчас файлик попался на глаза, почистил, обновил  и выложил. Не имея математического образования, заранее прошу прощения за отсутствие сложных математических выкладок, вызывающих у меня стойкий рвотный рефлекс. Всё написанное ниже носит скорее интуитивный  характер, никаким боком не претендует на истину  ”в последней инстанции”  и выложено  с целью сподвигнуть народ на комментарии  и  дополнения по существу (комментарии типа “нутыимудак” и “самтопонял чонаписал”, если можно, направляйте сразу в личку)
                       Опционный зигзаг в тезисах


( Читать дальше )

С практикующими трейдерами на опционном рынке хотелось бы пообщаться на тему сложных математических моделей. Сейчас известно несколько моделей, которые могут найти применение на практике. Например, модель Бруно Дюпире(http://www.globalriskguard.com/resources/deriv/pric_hedg_with_smile.pdf), stochastic vol model, local vol, модель хестона итд. Какие из них видите наиболее эффективными к примеру для использования на фортсе? Использует ли кто-нибудь методы эконометрики(Garch-и) в построении улыбок? Насколько это эффективно? Если у вас имеется модельный трейдинг, то насколько модель устойчива, есть ли проблемы с подгонкой параметров и производите ли переоптимизации модели в сложные периоды(рост волы, падение волы)? Какие программные средства используете для своих вычислений? Если не секрет программными продуктами какой компании пользуетесь или сами разрабатываете софт? 

Немного про свою торговлю. В модельном трейдинге я для себя нашёл пока одну единственную модель stochastic vol, которую согласуя с некоторыми расчётами, использую для построения смайла. Описание модели здесь 

( Читать дальше )

… на примере eur/usd (котировки с 1999 года для дней, недель и месяцев; часы и пятиминутки — по 65000 баров).

Во-первых, автокорреляция волатильности значительно сильнее для диапазонов типа high-low, чем для диапазонов close-open. Это довольно просто объяснить: если диапазоны  high-low детерминированы <только> прошлой волатильностью, то положение цен close и open относительно друг-друга и цен high и low «более случайно». Поясню: наприм., мы имеем ряд примерно одинаково длинных свечей, что приводит к высокой АК волатильности типа high-low. Но некоторые из этих свечей вероятно будут иметь длинные тела (close-open) с короткими тенями, а некоторые — короткие тела с длинными тенями. В этом случае АК диапазонов (close-open) неизбежно будет слабее.

Во-вторых, отсутствует четкая зависимость  АК диапазонов close-open (1) от АК диапазонов  high-low (2). Так для пятиминуток АК 1-го типа в 2,3 раза меньше АК 2-го типа. А для месячных цен — в 7,8 раз. Это объяснить гораздо труднее.



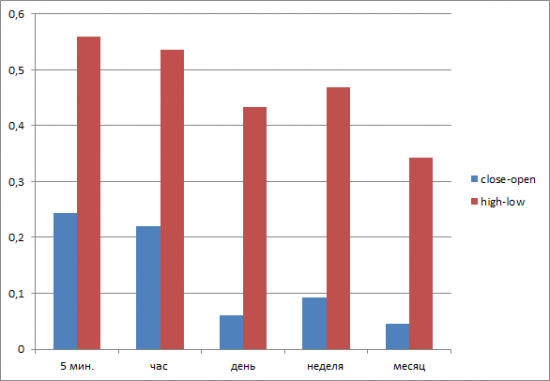
( Читать дальше )

Я предлагаю обзорные статьи по софту постить под отдельным тэгом = «трейдерский софт» Тогда мы получим хорошую тематическую ветку )

Итак, на данный момент я озабочен поиском новой платформы для анализа опционов на американском рынке. Одной из такой программ является Опшнвью. Ознакомится с ней можно при помощи вэбкастов:  www.discoveroptions.com/public/pages/education/archived_webcasts.html 

Меня же интересует мнение людей, кто уже пользуется этой программой —

1) в чём плюсы и минусы,
2) какие ньюансы с покупкой котировок — можно ли экспортировать дату из Interactive Brokers 
3) Какие альтернативы есть у данного софта

В общем рассказывайте всё что знаете — эта информация очень полезна трейдерскому сообществу.

Заранее говорю всем спасибо )

Попробуем сделать простейшую стратегию для долгосрочного инвестирования. В качестве рабочего будем использовать дневной таймфрейм. Вся суть стратегии будет заключаться в простейшей идеи, что падение рынка обычно связанно с более высокой волатильностью, чем в среднем. Соответсвенно, мы будем покупать, когда волатильность ниже среднего, и выходить из лонга когда она повышается. В качестве меры волатильности будем использовать размах бара High — Low. Остается вопрос лишь в том как измерить долгосрочное среднее волатильности. Можно использовать — среднее, то есть скользящую среднюю взятую за определенный период. Но так как мы имеем дело с распределением с тяжелыми хвостами, среднее будет плохой оценкой центра распределения. Поэтому будем использовать робастную оценку центра распределения — в нашем случаи это будет медиана, или более точно, скользящая медиана взятая с большим окном. Наши рассуждения достаточно напрямую транслируются в код на WealthLab:
 

using System.Collections.Generic;
using System.Text;
using System.Drawing;
using WealthLab;
using WealthLab.Indicators;

namespace WealthLab.Strategies
{
	public class MyStrategy : WealthScript
	{
		private StrategyParameter smaPeriod;
		public MyStrategy()
		{
			smaPeriod = CreateParameter("Range Sma Period", 1, 1, 50, 1);      
			
		}
		
		protected override void Execute()
		{
			DataSeries range = High - Low;
			DataSeries rangeSma = new WealthLab.Indicators.SMA(range, smaPeriod.ValueInt, "sma");
			DataSeries signal = rangeSma -  new WealthLab.Indicators.Median(range, 200, "median");
			
			for(int bar = 0; bar < Bars.Count; bar++)
			{				
				if (IsLastPositionActive)
				{
					//code your exit rules here
					if (signal[bar] > 0)
						SellAtMarket(bar + 1, LastPosition, "sell");
				}
				else
				{
					//code your entry rules here
					if (signal[bar] < 0)
						BuyAtMarket(bar + 1, "buy");
				}
			}
		}
	}
}

( Читать дальше )

Собственно, понятие коинтеграции и лежало, в основе статистического арбитража, который только начал появлятся в конце 80-х и позволил первопроходцам из JP Morgan, нарубить не мало денег, пока…, но об этом в конце статьи. Поэтому в этот раз мы поговорим, про коинтеграцию, что это такое, зачем и почему. Но начнем из далека и рассмотрим такие статистически понятия как порядок интеграции процесса, и фиктивной (spurios) регрессии, которые и лежат в основе. 

Рассмотрим для начала простейший процесс, гауссовский шум:


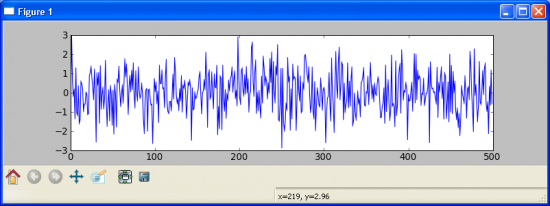
 Теперь построим его кумулятивную сумму, то есть возьмем значения и последовательно их сложим, таким образом получим что Y_i = sum k = 0..i X_k, где X_k — это исходный гаусовский шум, Y_i — результирующий процесс. То есть в данном случаи взяли шум и его проинтегрировали, таким образом получив случайное блуждание. Так же мы можем повторить данный процесс еще раз, но на этот раз взяв в качестве исходных значений, полученное нами на предыдущем шаги случайное блуждание. Таким образом получим (сверху — интеграл шума, случайное блуждание, снизу — повторная сумма но на этот раз взятая по случайному блужданию):

( Читать дальше )

Обещанное продолжение. Предыдущий пост из серии: http://smart-lab.ru/blog/43277.php 

В чем собственно смысл понятия авторегрессивности/автокорреляции/персистентности. Расмотрим простейший процесс в котором последующие приращения зависят от предыдущего. Обозначим приращение в момент времени t — X_t, в момент времени t + 1 — X_t+1. Соответственно мы хотим, чтобы приращение в момент времени t+1, каким то образом зависело от предыдущего t. Если выразить такую зависимость качественно, то у нас есть два варианта.

1) первый вариант, мы предполагаем что положительное приращение X_t должно увеличивать вероятность положительного приращения в следующий момент времени X_t+1, аналогично для  отрицательного. Проще говоря Х_t и X_t+1 положительно скоррелированны. Такая модель является «трендовой, персистентной», то есть покупая/продавая то что растет/падает мы смещаем вероятность выигрыша в свою сторону.

2)  второй вариант, мы предполагаем что положительные приращения X_t должны увеличивать вероятность отрицательных в момент времени X_t+1, а отрицательные приращения — положительных. То есть X_t и X_t+1 отрицательно скоррелированны. Такая моделья является «контр трендовой, анти-персистентной», то есть продавая то что выросло и покупаю то что упало, мы получаем статистическое преимущество. 

( Читать дальше )