Что бы почитать такого про бизнес?

Изучил книгу Элияху Голдратта «Я так и знал! Розничная торговля и теория ограничений». (Этому же автору принадлежат бестселлеры «Цель» и «Цель-2».)

Вкратце сюжет такой: семейная фирма владеет сетью магазинов по продаже текстиля. Вдруг в одном из магазинов прорывает трубу в подвале и затапливает склад с продукцией. Временная реорганизация склада, когда нужно избавиться от части товара, потому что его негде теперь хранить, приводит к парадоксальным результатам.

Прибыль магазина начинает расти, она достигает феноменальных процентов, и этот магазин, с затопленным складом, выходит на первое место во всей сети. Тут руководство спохватывается и, образно говоря, начинает чесать репу. Они начинают думать! Как же так могло получиться, что прорыв трубы привел к увеличению прибыли? Где тут собака зарыта? По ходу книги разворачивается целый детектив: лучшие умы компании пытаются понять, что же изменилось в работе этого магазина.

( Читать дальше )

Многие не понимают, почему в России падают реальные доходы населения.
Объясняю. Доходы населения состоят из большого числа компонентов. Зарплаты — далеко не единственный из них. 
Доходы населения это также:

-пенсии;
-все мыслимые социальные выплаты, пособия, субсидии;
-материнский капитал;
-дивиденды по акциям, купоны по облигациям, доходы от ОФЗ;
-проценты, которые капают по депозитам.

Реальные доходы населения — это доходы с учётом инфляции. Чтобы реальные доходы росли, доходы должны расти быстрее инфляции.
Что же происходит с доходами населения? Они падают, причём уже не первый год. 
Как я уже сказал, доходы населения состоят из многих компонентов. Например, зарплаты растут, причём довольно бурно. На графике Блумберга это чёрная линия. Они растут, опережая инфляцию.


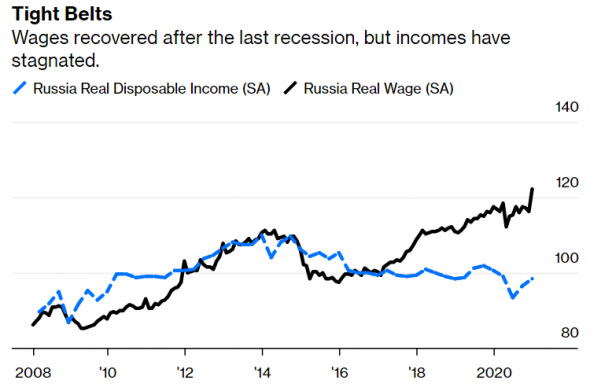
Синяя линия — это реальные доходы в целом. Они стагнируют и остаются в минусовой зоне.

( Читать дальше )

Самым успешным паевым инвестиционным фондом первого десятилетия этого века был CGM Focus Fund. За десять лет, охватывающих две рецессии, фонду удалось получить 18% годовой доход по сравнению с почти неизменной доходностью S&P 500. Это означает, что каждый доллар вначале превратился бы в более чем пять долларов в конце.

По иронии судьбы, согласно исследованию Morningstar, типичные инвесторы фонда тем временем теряли почти 11% ежегодно. Вы правильно прочитали — 18% прирост против 11% убытков.

Акционеры CGM Focus Fund не одиноки. Другие исследования показывают, что инвесторы в фонды акций в среднем уступают самому фонду (например, более чем на 6% в год в период с 1991 по 2010 год, согласно Davis Advisors). Причину нетрудно понять — люди особенно хорошо умеют покупать дорого и продавать дешево. Они легко подвергаются побуждению (от средств массовой информации, так называемых консультантов, друзей и соседей) к активной торговле, несмотря на взлеты и падения. 

( Читать дальше )

«ЛУКОЙЛ» сегодня, во второй половине дня, должен представить умеренные финансовые результаты за 4К20, продемонстрировав снижение EBITDA на 3% к/к на фоне существенного сокращения маржи переработки на фоне уверенной динамики в сегменте добычи. В итоге, мы ожидаем, что EBITDA 4К20 опустится немногим ниже 200 млрд руб. на фоне слабых показателей перерабатывающего бизнеса, поскольку крек-спреды в Европе существенно снизились, чему сопутствовало значительное снижение объёмов переработки нефти (последняя сократилась наполовину по предварительным операционным данным).

Несмотря на то, что маржа переработки за рубежом остается под сильным давлением в результате ощутимого отставания рынка моторного топлива от восстановления цен на нефть, фундаментальные показатели на сырьевом рынке продолжают улучшаться, подпитывая аппетит к высокомаржинальным баррелям компании. В результате роста нефтяных котировок восстановление показателей сегмента добычи в целом компенсировало слабую динамику переработки, что наглядно продемонстрировал рост квартальной выручки как в объемном, так и в стоимостном выражении.

Так, в сочетании с сильным ростом добычи газа в Узбекистане, мы прогнозируем сдержанное улучшение выручки, ожидая ее рост на 8% к/к до уровня порядка 1,5 трлн руб. (ниже на 18% г/г) на фоне роста продаж в добывающем сегменте. Учитывая умеренный доход от разницы валютных курсов по неоперационным статьям, мы ожидаем дальнейшего восстановления чистой прибыли, которая, по нашим оценкам, могла увеличиться на 46% к/к до 73 млрд руб., что предполагает прибыль на акцию в размере 110 руб.

Что касается движения денежных средств, мы ожидаем, что относительно слабая операционная динамика и сдержанный рост капиталовложений окажут давление на СДП, который должен составить 107 млрд руб., снизившись на 7% к/к, по нашим оценкам. Тем не менее, с учетом поправки на процентные расходы и арендные платежи, мы ожидаем, что скорректированный СДП опустится на 9,7% до 84 млрд руб., что предусматривает финальные дивиденды в размере 255 руб. на акцию по итогам 2П20 и привлекательные 300 руб. на акцию по итогам года. Если наши расчеты верны, дивидендная доходность акций Лукойла может составить порядка 4,8% в текущих ценах (к цене вчерашнего закрытия рынка Московской Биржи).

Блохин Никита
«Альфа-Банк»

И снова здравствуйте, хлопчики.   Если помните, 4 марта  с.г. я сделал половинки сделок   ( купил ГМК) и показал их  прилюдно.  
Население требовала не конечный результат, а начало сделки показать. Что я и 4 марта продемонстрировал. \Вот ссылка на 4 марта.

Теперь смотрите скрин от сегодня:   

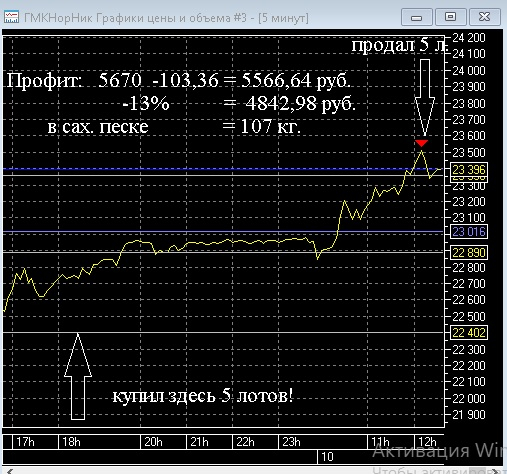
Вот я при обществе закрыл открытую 4 марта покупку 5 лотов ГМК.   В результате получил ( и все участники моего закрытого чата, кто повторил за мной )  чистыми 4842,98 рубля или в сахарном песке  107 кг. Это два мешка по 50 кг и 7 кг. довесок. Хлопчики могуь сами посчитать, сколько годовых сегодня заработали участники закрытого канала телеграм.
   
Итак, показана сделка снова в плюс. Теперь верите, что у меня весь 2020 год шли  сделки все в  плюс и также с начала этого года тоже в плюс. 
    Наконец, я всем доказал и обосновал, что мои сделки все в плюс. 

( Читать дальше )

Разгребая старые документы, нашли выписку по первой ипотеке.

Объект: 3-комнатная квартира в 5-этажном панельном доме в Саратове, 60 кв. м

Начало: 09.12.2011

Срок: 10 лет

Стоимость квартиры: 1'720'000₽

Размер ипотечного кредита: 1'000'000₽

Процентная ставка: 11,70% годовых

Ежемесячный платёж: 14'174₽

UPD.: многие интересуются, что с ней стало. Писал об этом полгода назад здесь, на смарт-лабе

Действие происходило в Саратове.

У нас после свадьбы на руках оказалось примерно 220'000₽ (накопления + подарки), и родители жены любезно нам предоставили 500'000₽ на первоначальный взнос. Стоит отметить, что это была единственная такая материальная помощь за всю жизнь, и впоследствии подобного больше не было (предложения были, но мы отказывались). Кто-то скажет, что 1 млн ₽ — это мало, не то что нынешние ипотеки. Надо понимать, что 1 млн ₽ в 2011 году — это не то же самое, что 1 млн ₽ в 2021 году, да и уровень наших з/п оставлял желать лучшего.

( Читать дальше )

XAUUSD

Реализация сценария: успешно

Предположения о продолжении снижения в прошлом обзоре подтвердились. Золото действительно продолжило нисходящее движение, пусть и без предварительной коррекции к сопротивлению на 1752, тем самым отработав целевую область между 1692 и 1682. Таким образом, сценарий можно считать исполненным успешно.

Сразу по достижении уровня 1682 цена остановилась, а потом начала разворачиваться и расти, отыграв обратно часть снижения. Это может намекать либо на локальное развитие восходящей коррекции, либо полноценный разворот вверх ввиду окончания нисходящей коррекции. Можно предположить, что, как минимум еще одна восходящая волна может реализоваться.

Прогноз: разворот на восходящее движение

( Читать дальше )

Один из крупнейших российских авиаперевозчиков «Аэрофлот», акции которого находятся у нас в покрытии, представит 10 марта свои финансовые результаты по МСФО за четвертый квартал и весь 2020 год.

Ранее компания опубликовала финансовые результаты своей деятельности в соответствии с Российскими стандартами бухгалтерского учета (РСБУ). Выручка «Аэрофлота» за двенадцать месяцев снизилась на 58,4% г/г и составила 229,8 млрд руб. Тем не менее, после катастрофического сокращения объема авиаперевозок в марте и апреле минувшего года сформировался тренд на сокращение темпов снижения выручки, и за четвертый квартал выручка сократилась на 59,2% г/г против — 67,4% г/г в третьем квартале и -85,0% г/г во втором квартале 2020 года. Поддержку выручке в последние три месяца коронакризисного года оказало постепенное восстановление международного авиасообщения и активный рост выручки от сегмента грузовых перевозок (+78% г/г). Тем не менее, чистый убыток компании по итогам 2020 года составил 96,5 млрд руб. против прибыли в 5,3 млрд руб. в 2019 году.

Операционные показатели «Аэрофлота» за 2020 год показали, что общий объем перевозок составил 30,2 млн пассажиров, что на 50,3% ниже показателя предыдущего года. На внутренних линиях авиакомпаниями группы было перевезено 24,2 млн пассажиров, что на 28,1% ниже показателя предыдущего года. При этом лоукостер «Победа» перевез 9,1 млн пассажиров, что лишь на 11,7% ниже результата 2019 года.

Резюмируя вышесказанное, мы ожидаем, что финансовые показатели «Аэрофлота» по МСФО за четвертый квартал и весь 2020 года будут значительно ниже значений за 2019 год вследствие негативного глобального воздействия пандемии коронавируса на авиаотрасль. Тем не менее, с учетом массовой вакцинации, постепенным снятием локдаунов и выходом экономики из рецессии мы полагаем, что худшее для компании уже позади, и бизнес «Аэрофлота» вернется к докризисным уровням в среднесрочной перспективе. Точкой роста группы продолжит оставаться авиакомпания «Победа», которая уже в январе 2021 года нарастила пассажиропоток на 43,7% г/г и перевезла 689,1 тыс. человек, продемонстрировав лучшую динамику среди российских перевозчиков по количеству перевезенных пассажиров.

Наша рекомендация «Покупать» по бумагам «Аэрофлота» с целевой ценой 116 руб. за акцию на конец 2022 года подразумевает потенциал роста на 66% от текущего ценового уровня.

Пырьева Наталия
ГК «Финам»

Прошлая статья, посвященная бедности в России. Вызвала много споров. Настолько много что я принял решение написать еще одну часть. Где еще более детально рассмотреть феномен экономического кризиса в России.
Так по данным Росстата падение экономики России по итогам уже прошедшего 2020-го года. Стало максимальным за последние одиннадцать лет.  Падение вызвали следующие факторы  — эпидемия коронавируса, ограничения вызванные эпидемией,  и новой волной снижения цен на нефть.



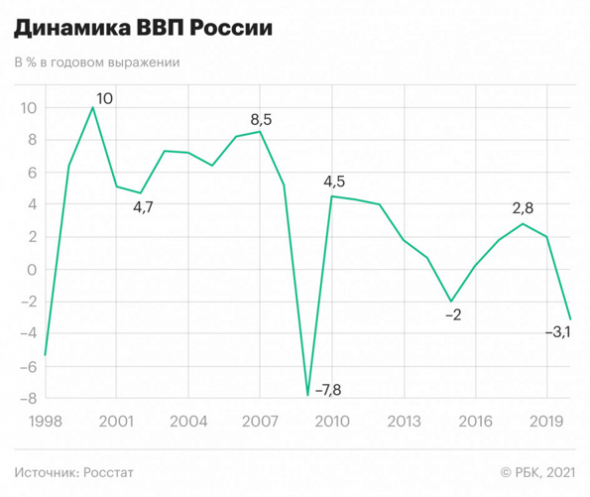
( Читать дальше )

Фонды Тинькофф переходят на золото на Московской бирже — почему это важно?

Тинькофф Капитал стала участником торгов на рынке драгоценных металлов на Московской бирже.

Что это значит для инвестора?

Наш биржевой фонд «Тинькофф Золото» (TGLD) постепенно уходит от инвестиций в золотые слитки через акции iShares Gold Trust. Вместо этого он начнет покупать физическое золото на Московской бирже. То же самое будут делать и Вечные портфели в рублях, долларах и евро (TRUR, TUSD, TEUR), у которых золото традиционно занимает четверть портфеля.

Они собираются по принципу:

Стратегия для любой ситуации в экономикеИнвестиции делятся на равные доли: золото, акции, облигации и деньги. Такая стратегия помогает получать прибыль в любых условиях: при росте, стагнации или спаде экономикиwww.tinkoff.ru/invest/news/555786/

( Читать дальше )