Был у меня давно граальный алгоритм для fRTS. Работал в плюс без подстроек годами, но вот в 2015 году что-то случилось… как не тужся, но параметры алгоритма оптимизированные на предыдущих годах к 2015 году не подходят:

 

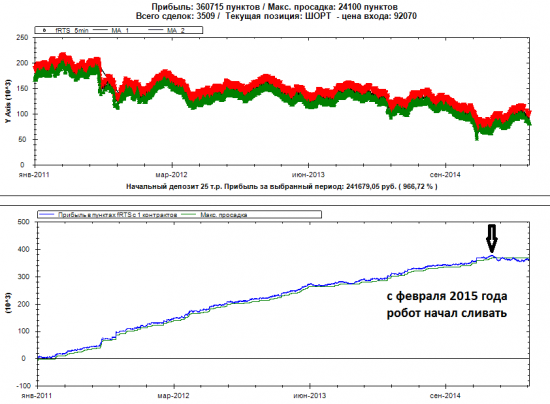
фишка была в том, что сам алгоритм примитивен до опупения… но работал..

вся логика — 5 строк кода 

if (pr > max) { max = pr; ind = 1; }   // — если обновляем максимум то в лонг
if (pr < min) { min  = pr; ind = -1; }  // — если обновляем минимум то в шорт

max -= k2;   // максимум плавно опускаем каждую 5-минутку
min += k3;  // минимум плавно поднимаем каждую 5-минутку

if ((ind == 1) && (pr < max- stop_long)) ind = 0;  // если цена ниже максимума на размер стопа и мы лонге — выход кеш

( Читать дальше )

В прошлый раз, рассматривая подбор наилучшей позы на примере продажи волатильности, сделал неверный вывод о том, что оптимальная позиция должна походить на форму распределения P. Cделал его под влиянием книги: Опционы: Системный подход к инвестициям. С. Израйлевич, В. Цудикман (см. скриншот 103 стр. из книги). Но Михаил, спасибо, поправил и подсказал, что лучшая комбинация зависит не столько от собственного прогноза P, а скорее от разности своего прогноза и рыночного. Проверим это предположение и рассмотрим несколько стратегий, для каждой найдем оптимальную позицию и сравним ее с разностью (P-Q). Стратегии предлагаю такие: продажа и покупка волатильности, направленная торговля БА и сценарный подход.

Начнем с продажи волатильности. Берем рыночное распределение Q и сжимаем его (поскольку считаем, что рынок ошибается, и волатильность на самом деле меньше):

 

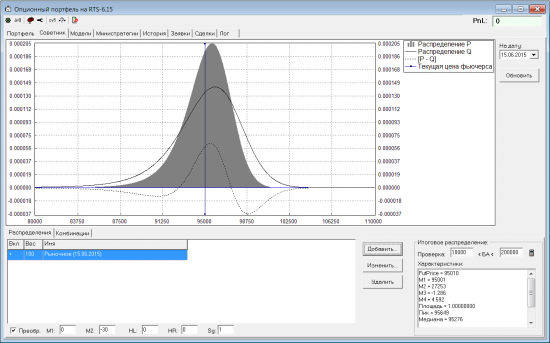
Сплошная серая заливка у распределения P (наш прогноз), тонкая сплошная линия — распределение Q (прогноз рынка), пунктирная линия — разница между нашим прогнозом и рынком.

Посмотрим, какую оптимальную позицию для такого случая находит геналгоритм:
 

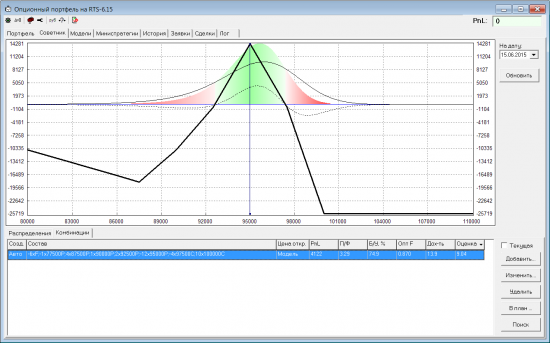
Видно, что профиль на экспирацию у найденной позы имеет положительный PnL как раз там, где P-Q > 0.

( Читать дальше )

После рассмотрения основ машинного обучения в первой части, мы перейдем к примеру использования наивного байесовского классификатора для предсказания направления движения цены акций Apple. Сначала разберем основные принципы работы наивного байесовского классификатора, затем создадим простой пример использования дня недели для предсказания направления цены закрытия — выше или ниже текущей, а в окончании построим более сложную модель, включающую технические индикаторы.

Что представляет собой наивный байесовский классификатор (НБК)?

НБК старается найти вероятность события А при условии, что событие В уже произошло, обзначаемую как Р(А|B) (вероятность А при условии В).

В нашем случае, мы должны спросить: какова вероятность того, что  цена возрастет, при условии, что сегодня — среда? НБК берет во внимание обе вероятности — общую вероятность роста цены, то есть число дней, когда цена закрытия была выше цены открытия относительно всех рассматриваемых дней, и вероятность роста цены при условии, что сегодня среда, то есть сколько прошедших сред имело цену закрытия выше цены открытия?

( Читать дальше )

В последнее время приобретают все большую популярность алгоритмы машинного обучения. Они применяются для решения задачи классификации входных данных, или, проще говоря, выявления паттернов в структуре этих данных. Небольшой цикл статей про машинное обучение опубликован на сайте inovancetech.com, здесь я представляю их перевод.

В этой серии статей мы рассмотрим построение и тестирование простой стратегии машинного обучения. В первой части отметим основные принципы машинного обучения и их применение к финансовым рынкам.

Машинное обучение становится одной из самых многообещающих областей в алгоритмической торговле за последние два года, но имеет репутацию слишком сложного математического подхода. В действительности это не столь трудно в практическом применении.

Цель машинного обучения (МО) в том, чтобы правильно смоделировать исторические данные, и затем использовать эту модель в предсказании будущего. В алгоритмической торговле применяется два типа МО:

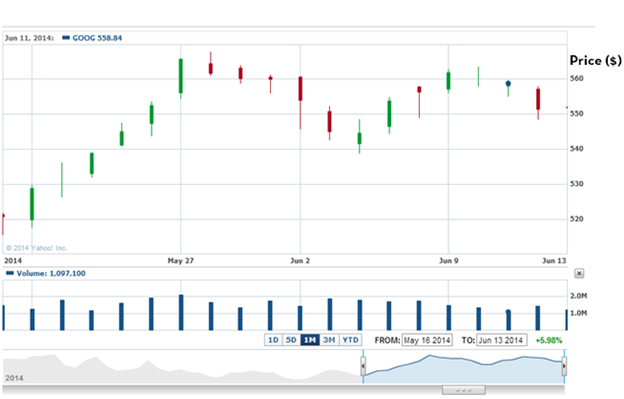
• Регрессия: используется для предсказания направления и амплитуды исследуемой величины. Например, цена акций Гугл возрастет на 7 долларов на следующий день.
• Классификация: используется для предсказания категории, например, направления движения цены акций Гугл на следующий день.

( Читать дальше )

  В процессе поиска собственной системы торговли я перепробовал довольно много всего, сейчас я могу сказать, что являюсь сторонником системной торговли и алготрейдинга. Одним из побочных результатов этого «увлечения» стало написание забавной программки с графическим интерфейсом, значительно облегчающей системную торговлю внутри дня, о которой я расскажу в этой статье после небольшого предисловия.

( Читать дальше )

Есть мнение, что сделать робота очень сложно. Это под силу только крутым программистам. Попробую опровергнуть — чтобы сделать робота достаточно уметь хорошо пользоваться поиском и знать азы программирования в рамках школьной/институтской программы.
Большинство задач решается операторами if, while, repeat и иногда  for. Плюс специфические функции для взаимодействия с торговой платформой.
Будет этот робот зарабатывать или нет зависит уже не от навыков програмирования, а от заложенной в него логики.
Напишем простейшего робота на qlua для Квика, который будет покупать/продавать волатильность на опционах
путем покупки синтетического стрэдла www.option.ru/glossary/strategy/long-straddle
или продажи синтетического стрэдла www.option.ru/glossary/strategy/short-straddle

( Читать дальше )

  Все наверное знакомы с таким понятием как парный трейдинг, как правило данный способ торговли используют на линейных, более или менее коррелированных инструментых, например; акция/фьючерс на нее, или фьючерс на индекс/акции входящие в индекс и т.д.

Метод торговли прекрасно работает до резкой раздвижки спреда, которая рано или поздно происходит, если бы не раздвижка — был бы грааль 100%.

Как же избавиться от недостатков данного метода, сохранив все его достоинства, при  этом главный недостаток (раздвижка спреда) сделать самой большой возможностью заработать?

Все просто, нужно применить навыки парного трейдинга на опционах! 

Берем разные страйки одного б/а и, создаем график спреда между страйками, создаем 2 позиции как на картинках ниже, и спокойно торгуем спред откусывая понемногу профита и с нетерпением ждем резкой раздвижки спреда которая нам позволит как минимум заработать десятки процентов к депозиту!

То есть что мы имеем в итоге:  при флете б/а мы зарабатываем по немногу на спреде (главное не теряем), при резком движении б/а мы очень хорошо зарабатываем, позицию лучше делать максимально дельта и тетта нетральной.

( Читать дальше )

Вузы США:

1. Introduction to Computational Finance and Financial Econometrics (University Of Washington)

https://www.coursera.org/course/compfinance

2. STOCKS AND BONDS: RISKS AND RETURNS (Stanford U) 

http://online.stanford.edu/Stocks_and_Bonds_Fall_2014?utm_source=vpol&utm_medium=email&utm_term=mailer&utm_content=learning%2520opportunities&utm_campaign=stanford%2520online

3. Computational Investing, Part I (Georgia Tech) 

https://www.coursera.org/gatech

4. Financial Engineering and Risk Management Part I (Columbia U) 

https://www.coursera.org/course/fe1

5. Financial Engineering and Risk Management Part II (Columbia U) 

https://www.coursera.org/course/fe2

6. Asset Pricing, Part 1 (The University of Chicago) 

https://www.coursera.org/course/assetpricing

7.  Option Pricing  (Cal Tech) 

https://www.edx.org/course/caltechx/caltechx-bem1105x-pricing-options-2786

( Читать дальше )

Всем доброго времени суток

На днях подвел итоги 1,5 лет роботорговли:

• использую систему Давида Серебренникова, подробно описанную в  его блоге. Давид, если вдруг читаете эти строки — еще раз Вам большое спасибо за публикации
  
• активная внутридневная торговля фьючерсами в связке Amibroker+QUIK с переносом позиций
  
• торговля с реинвестированием, деньги в этот период со счета не выводились
  

( Читать дальше )

Несколько раз встречал мнение, что дельта по БШ — дюже неправильная. Решил покопать эту тему. Для начала, научился самостоятельно подбирать параметры для кривой волатильности по биржевой формуле (там где арктангес). Получилось вот так:

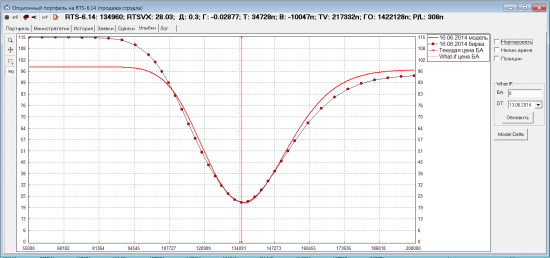
Здесь на хвостах довольно большое отличие от биржевой улыбки, но если это пересчитать в пункты временной стоимости, то разница совсем незначительная.
 
После этого сделал простенькую модель движения улыбки: центр новой улыбки будет перемещаться по исходной улыбке. Например, если сегодня БА=120000, то модельная улыбка переместится так:

( Читать дальше )