В последние дни было заметное количество серьезных содержательных сообщений по опционам. Большое спасибо всем авторам.

 

Чтобы немного разбавить сухую академическую теорию, небольшая зарисовка из жизни реальной проданной позиции в момент выхода сильной новости с последующим резким движением рынка. Дело было 20 марта 2019 года в 21:00 МСК. На заседании FED вдруг смягчили риторику и вообще высказались в таком духе, что «мы так больше не будем».


Ролик 1:25, лучше смотреть в качестве HD1080: будут лучше видны числа.

( Читать дальше )

Раз тут возник диспут «Нафига козе баян» (Зачем ОФЗ минфину во время профицита бюджета)
Вынесу ка я в отдельную тему базовые моменты концепции таргетирования инфляции и стерилизации денежной массы.

Сначала теоретическая часть, ее я честно сплагиатил (позаимствовал из прошлых времен)
Те кому лень читать много букв саммари:

— концепция регулирования со стороны ЦБ сейчас — таргетирование инфляции.
Другими словами, основная задача удержать инфляцию (номинальную) в заданных параметрах любой ценой.
Стерилизация денежной массы — это создание условий при которых свободная ликвидности изымается из реальной экономики и «связывается» максимально долгосрочно в финансовом секторе.



Грубо говоря человек имеющий свободные средства размещает из на депозите, в ОФЗ и т.д и живет на % — пока ему этого %та хватает на жизнь он не пытается купить бетон, открыть автомойку, пекарню и т.д.

( Читать дальше )

Перед началом нашей тусовки я решил выложить конспект или обозрение, о чем я хотел сказать.

План

Мне очень сложно судить о публике. Поэтому зайдем издалека. Я не буду говорить, что рынок случает. Хотя тема интересная. Меня убедили. Только остался один вопрос. Как те, которые знают, что рынок не случаен, совершают отрицательные сделки. То есть встают с утра и зная, что сегодня в вверх, поэтому надо продавать, а то на рынке деньги закончатся и я не смогу больше зарабатывать. Но не будем об этом. Скажем так рынок вероятностный. Соответственно мы будем использовать закономерности из теории вероятности. Предмет нашего рассмотрения это логприращения к цене БА. То есть мы берем логарифм цены закрытия сегодня и отнимаем логарифм закрытия цены вчера. Получается число. Почему логарифм, я раскрывать не буду, а то мы уйдем в дифуры. Но, скажем, это удобно. Мы потом можем суммировать все числа и получить изменение за период. Это проще чем проценты. Второе, что мы возьмем, это квадрат этого приращения или второй момент.  Это нам позволит сравнивать средние значения и оценивать разброс.

( Читать дальше )

Предыдущее мое произведение про продажу крайних опционов было отмечено плюсиками более 50 человек.  Меня это удивило и обрадовало, поскольку я не предполагал, что такое большое количество людей на смартлабе не просто интересуются опционами, но и разбираются в некоторых особенностях торговли этим инструментом. До этого у меня было впечатление, что опционами на смартлабе торгуют чуть больше десяти человек.

В продолжение прошлой темы, хочу предложить вам на рассмотрение некоторые рассуждения о том, какие опционы выгоднее продавать.

Определимся с терминами и понятиями, которые будем рассматривать:

[Тэта] -  потеря стоимости опциона за определенный промежуток времени [t]

У нас есть текущая волатильность базового актива. Исходя из этой волатильности, мы можем посчитать ожидаемый средний путь, который пройдет цена базового актива за время [t]. Этот путь назовем

( Читать дальше )

( Читать дальше )

На моих курсах часто звучит претензия, что мало картинок, нет наглядности, где входить, где выходить. Вот решил привести пример одного дня.

RIH9 тренд (на утро в лонге 3 из 4, 1 с 03.01, 1 с 04.01, 1 с 10.01) и контртренд (на утро шорт 1 вход на вечерке). Тренд не торговался



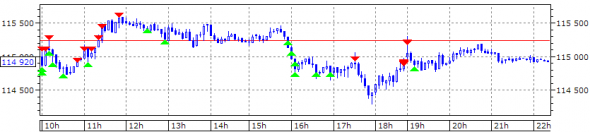
Итого тренд без изменений, контртренд 1 лонг

SiH9 тренд (на утро лонг 1 из 1 с 09.01)



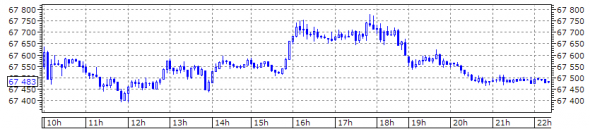
( Читать дальше )

В одном из предыдущих постов писал про Google Colab — бесплатный доступ к интерактивной среде Jupyter Notebook на языке Python с кучей библиотек для анализа данных (и самой популярной — Pandas: обучалки-введение).
   Низкий порог входа в мир серьёзного анализа данных -тем и привлекателен этот зоопарк. Несколько строк кода и уже можно анализировать-смотреть данные (акции, облигации, фьючи, макро).

   Если вы пробовали писать скрипты в Excel, кастомные индикаторы в Мультичартсах или Метастоках, то освоить язык Python в интерактивной среде Jupyter Notebook (Google Colab — даёт бесплатный доступ) — посильное занятие.
   Для американского рынка есть библиотека (-ки), которые позволяют подкачать биржевые и экономические данные — я писал об этом. Кстати к 

( Читать дальше )

На данный момент в недельных сериях опционов в связи с праздниками не удобно создавать какие-либо позиции. Поэтому, примеры будут на месячных опционах. На недельных всё то же самое но в четыре раза быстрее и дешевле по премиям.

Первое, что пытаются делать трейдеры при направленной торговле опционами, это купить опцион в предполагаемом направлении движения базового актива. При ожидаемом росте – купить колл, при ожидаемом падении – купить пут. Чаще всего, если движение базового актива было не достаточно сильным, такая позиция приносит убыток. Это происходит потому, что со временем опцион теряет свою цену. Называют это временным распадом опциона. Но есть способ избавиться от такого негативного влияния времени.

Основная идея заключается в следующем: Производится покупка опционов с более дальним сроком исполнения и одновременно с этим, для компенсации временного распада, продаются опционы с более близким сроком исполнения.

( Читать дальше )

Почти все торговые системы одного инструмента, основанные на анализе прошлых цен сделок по этому инструменту, можно классифицировать на два идейных типа.
1. Трендовые. Это когда если когда-то в каком-то смысле цена выросла, то покупаем. Если когда-то в каком-то смысле цена упала, то продаем.
2. Контртрендовые. Это когда если когда-то в каком-то смысле цена выросла, то продаем. Если когда-то в каком-то смысле цена упала, то покупаем.
Конечно, есть и смешанные, например, лонг по пересечению МА вверх и выход по тейкпрофиту. Вход здесь трендовый, выход--контртрендовый. И почти любая сложная система будет использовать как трендовые, так и контртрендовые идеи. Но здесь мы обсудим именно идейную классификацию.  

В идеальном мире неэффективностей, связанных с отклонением от беспамятного броуновского движения, без разницы какая неэффективность--трендовая или контрендовая. Например, вот здесь она контртрендовая: https://smart-lab.ru/blog/186186.php. Ну и отличный граальчик выходит, жаль что это модель всего лишь. В реальной жизни однако неэффективности не есть отклонение от броуновского движения. То, что рынок так похож на броуновское движение--это следствие того, что все торгующие постоянно ищут неэффективности (в широком смысле, если по простому, то ищут где бы добыть бабла). То есть «броуновость» рынка в каком-то смысле может быть неплохо описана моделью среднего поля, когда из-за невозможности разобраться в действиях отдельных торгующих вводят некую эффективную величину. Благо на рынке это сделать очень просто, там ничего и придумывать не надо, эта эффективная величина--цена. То есть неэффективность в реальном рынке--это не отклонение от броуновского движения, это скорее отклонение от усредненного по всем неэффективностям состояния. С этой точки зрения рынок--это такая суперпозиция поисков неэффективностей (то есть поисков бабла) различного калибра и известности, каждая из которых торгуется своим кругом торгующих со своими финансовыми, умственными и другими возможностями. 

( Читать дальше )

Оптимальное количество бумаг в портфеле

         
          Очень часто, когда заходит речь о диверсификации, на лице слушателя появляется скептическая улыбка. Казалось бы, что тут можно придумать нового: все уже давным-давно известно, писано и переписано тысячами трейдеров. Если вкратце резюмировать суть большинства рассуждений на тему диверсификации, то можно выделить две основные идеи:

1. Диверсификация необходима.
2. Избыточная диверсификация неэффективна, ибо не позволяет много заработать.

         Не знаю как вас, а меня всегда интересовал вопрос: каким же должно быть оптимальное количество различных бумаг в портфеле? Интуитивно кажется понятным, что если все деньги поставить на одну бумагу, то риск будет очень велик, и подобная торговля уже сильно смахивает на лотерею (угадал/не угадал). С другой стороны, если купить акции около 100 различных компаний, то, помимо проблем с управлением и анализом такого большого портфеля, рассчитывать на приличную доходность тоже можно с большой натяжкой. Как же быть? Сколько бумаг покупать? Прежде чем дать свой ответ на этот вопрос, мне кажется необходимым сделать небольшую оговорку: я вполне отдаю себе отчет, что каждый раз бывает по-разному, иногда портфель, сформированный из всего 2 бумаг, обгонит портфель из 10 бумаг, а когда-то будет наоборот. Тем не менее, мне хотелось бы провести исследование на статистических данных для ответа на вопрос, какое же число бумаг будет оптимальным наиболее часто или даже точнее будет сказать так: какой интервал бумаг (от и до, например от 6 до 10, или от 10 до 15 и т.д.) обеспечит наибольшую доходность.

( Читать дальше )