Кирилл Браулов
Точность прогноза
- 27 июня 2015, 01:17
- |
Допустим, есть две системы, которые выдают прогноз — где будет БА на экспирацию. Прогноз выдается в виде распределения вероятностей. Задача: оценить на истории — какая система выдает более точный прогноз.
Вот картинка для иллюстрации. Слева график цены БА, справа два графика плотности вероятности, синий для распределения P, зеленый для распределения Q. Красным кружочком отмечен уровень S, где реально оказалась прогнозируемая цена:
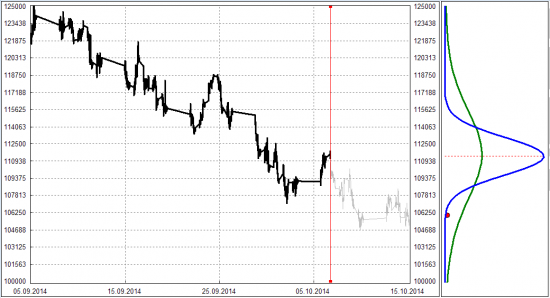
Для оценки точности прогноза пробовал считать средний квадрат отклонения распределения от S (кажется, этот метод называется MSE). Для вышеприведенной картинки такое отклонение меньше у распределения P. Но, мне кажется, что распределение Q более точное: оно дает гораздо большую вероятность для красного кружочка.
Может кто подскажет — можно ли как-то по другому считать точность распределения-прогноза?
- комментировать
- ★4
- Комментарии ( 40 )
Оптимальная опционная позиция: общий принцип
- 14 июня 2015, 14:18
- |
В прошлый раз, рассматривая подбор наилучшей позы на примере продажи волатильности, сделал неверный вывод о том, что оптимальная позиция должна походить на форму распределения P. Cделал его под влиянием книги: Опционы: Системный подход к инвестициям. С. Израйлевич, В. Цудикман (см. скриншот 103 стр. из книги). Но Михаил, спасибо, поправил и подсказал, что лучшая комбинация зависит не столько от собственного прогноза P, а скорее от разности своего прогноза и рыночного. Проверим это предположение и рассмотрим несколько стратегий, для каждой найдем оптимальную позицию и сравним ее с разностью (P-Q). Стратегии предлагаю такие: продажа и покупка волатильности, направленная торговля БА и сценарный подход.
Начнем с продажи волатильности. Берем рыночное распределение Q и сжимаем его (поскольку считаем, что рынок ошибается, и волатильность на самом деле меньше):
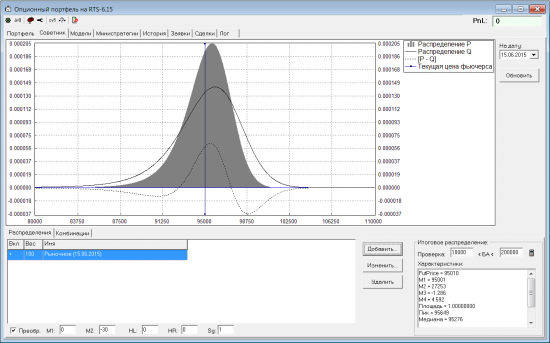
Сплошная серая заливка у распределения P (наш прогноз), тонкая сплошная линия — распределение Q (прогноз рынка), пунктирная линия — разница между нашим прогнозом и рынком.
Посмотрим, какую оптимальную позицию для такого случая находит геналгоритм:
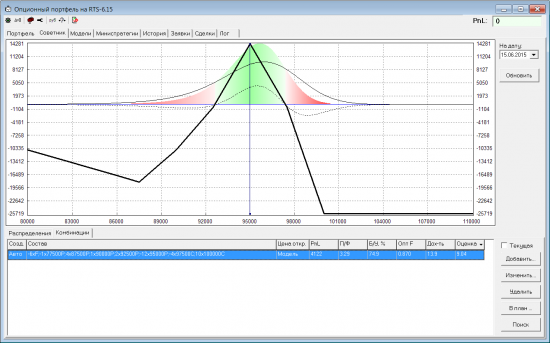
Видно, что профиль на экспирацию у найденной позы имеет положительный PnL как раз там, где P-Q > 0.
( Читать дальше )
Продажа волатильности, управление позицией
- 01 июня 2015, 16:42
- |
В продолжение топика Продажа волатильности, оптимальная позиция. Попробуем теперь смоделировать управление позицией при продаже волатильности и понять что лучше: дельтахедж фьючом, роллирование или что-то другое. За основу возьмем проданный стрэддл. Хотя предыдущий анализ показывает, что это не самая оптимальная поза при продаже волы — для простоты исследования возьмем именно ее.
Зададим для автоматического поиска NStrike = 1 и получаем такую позу:

Возьмем ее за основу и фиксируем цены открытия. Теперь смоделируем перемещение БА на страйк влево. Сделаем это переносом распределения Q (которое используется для получения текущих цен с рынка). Распределение P получим из нового Q сжатием (т.е. по прежнему считаем что дисперсия у рыночного распределения завышена и поэтому остаемся в продаже волы). Оценка зафиксированной позы сильно упала (с 2.37 на 0.84), но пока еще осталась положительной:
( Читать дальше )
Продажа волатильности, оптимальная позиция
- 31 мая 2015, 21:49
- |
При продаже волатильности возникает вопрос — какую позицию лучше всего открыть? Можно продать просто стрэддл на центральном страйке. Но есть ведь много других вариантов. Предлагаю анализ-сравнение различных позиций и поиск лучшей. Анализ сделан на основе распределения вероятностей, где будет БА на экспирацию.
Рассмотрим сначала четыре стандартных варианта: шорт стрэддл, шорт стрэнгл, лонг бабочка и лонг кондор.
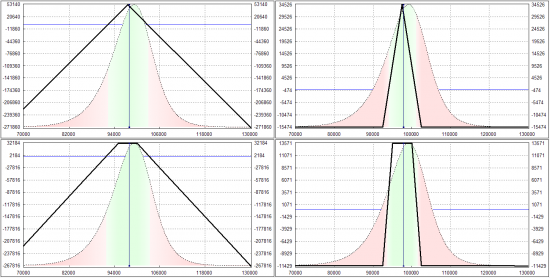
Для анализа будем использовать два распределения:
- Распределение P — отражает наше мнение о том, где будет БА на экспу.
- Распределение Q — отражает текущее суммарное мнение рынка о том, где будет БА на экспирацию (если посчитать справедливые цены опционов по Q, то все они будут находиться примерно между текущими бид-асками в стаканах на всех страйках выбранной серии).
( Читать дальше )
Оптимальная доля счета для торговли
- 05 марта 2015, 18:50
- |
Чтобы лучше понять, насколько важна используемая доля счета, временно отойдем от опционов и рассмотрим игру, которую предложил Ральф Винс в своей книге «Математика управления капиталом». Ставим на кон какую-то долю от счета и с вероятностью 50% либо утраиваем поставленные деньги, либо их проигрываем. Матожидание у такой игры положительное, и очевидно, что тут можно хорошо заработать. Но вот какую долю от имеющихся денег ставить каждый раз на кон? Если делать слишком маленькую ставку, то выигрыш будет, но небольшой, и пользы будет мало. Если увеличивать долю поставленных денег, то счет будет расти все быстрее. Но, с другой стороны, если поставить слишком большую долю, например, каждый раз ставить всю имеющуюся сумму, то с вероятностью 50% она будет потеряна. Т.е. игра для нас окажется совсем
( Читать дальше )
Направленная торговля опционами
- 24 февраля 2015, 02:34
- |
Предлагаю обсудить одну идею направленной торговли опционами. Прочитал о ней в книге «Опционы. Системный подход к инвестициям. С. Израилевич, В. Цудикман» (спасибо Стасу за наводку) и загорелся попробовать. Слегка доработал, частично реализовал и хотел бы поделиться промежуточными результатами. Буду рад любой критике, новым идеям и т.д.
Суть идеи в том, чтобы по распределению вероятностей оценивать различные опционные позиции и выбирать лучшие из них. Для иллюстрации рассмотрим позицию «голый фьючерс» на основе рыночного распределения:
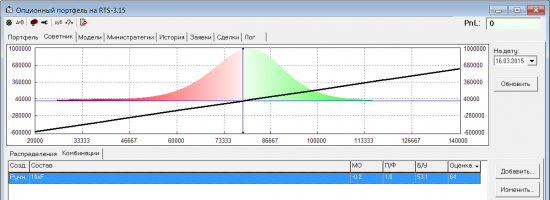
Вот какие показатели можно рассчитать по распределению:
- Матожидание PnL (МО) — среднее PnL всех возможных исходов считается как интеграл произведения платежной ф-ции на экспу на функцию плотности
( Читать дальше )
Усреднение против рынка
- 16 января 2015, 04:56
- |
В качестве начальной позы рассмотрим продажу 100 контрактов Si-3.15 по цене 67280:

Кто не знаком с профилем PnL (Profit And Loss) опционного портфеля: жирная черная линия с отрицательным наклоном показывает PnL проданного фьючерса, при падении Si PnL портфеля растет, при росте — PnL падает.
Используя распределение вероятностей можно посчитать вероятность того, что на экспирацию мы будем в безубытке (PnL >= 0). Считается просто как площадь под распределением от 0 до 67280. Для начальной позы получаем вероятность Б/У=58.5% (не 50% поскольку распределение несимметричное). Кроме того, зададим для портфеля недопустимые потери на уровне 5000000р. Все что выше назовем крахом. По распределению посчитаем вероятность краха (площадь под распределением от 117280 до +беск). Получилось 1.2%.
( Читать дальше )
Анализ опционной позиции через распределение вероятностей
- 10 декабря 2014, 22:29
- |
Для примера решил рассмотреть позицию зигзаг:
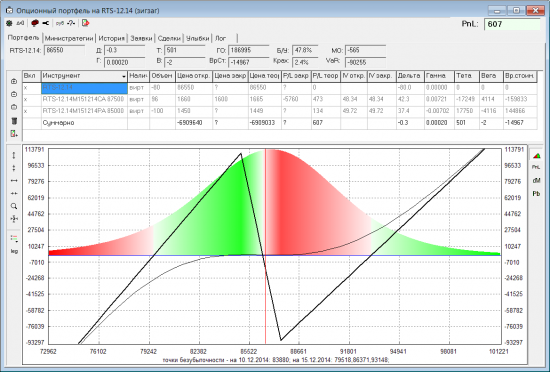
Пропорции в этой позе подобрал так, чтобы дельта и вега (по БШ) были равны нулю. Т.е. с точки зрения БШ, позиция — нейтральная.
Имея распределение вероятностей, мы можем посчитать различные оценки нашей опционной позиции, такие как:
- вероятность безубытка на экспу (площадь под зелеными участками распределения)
- вероятность краха (если задать размер недопустимых потерь для портфеля)
- матожидание PnL
- текущий PnL
( Читать дальше )
Модель Хестона и гэпы
- 27 октября 2014, 04:30
- |
Одна из ошибок того исследования была в предположении, что существует некая инерция в движениях цены БА: чем больше очередное приращение цены, тем больше вероятность что следующее приращение продолжится в том же направлении. Именно добавление этого эффекта в модель давало толстые хвосты и изгиб улыбки параболой. Но более внимательный анализ истории показал, что этого эффекта не наблюдается. Каким бы большим не было приращение — матожидание следующего будет ровно 0.
Но главной ошибкой было использование эмпирического распределения приращений для построения распределения цен на экспу. Понять что это ошибка, помогла всего одна фраза от
( Читать дальше )
Прогноз улыбки и "правильная" дельта
- 13 июня 2014, 16:03
- |
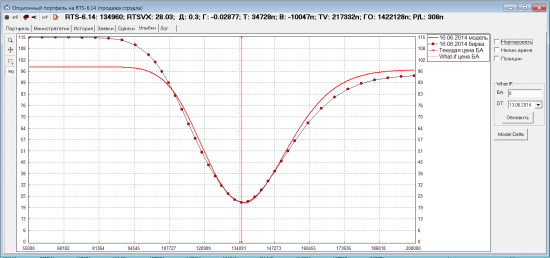
Здесь на хвостах довольно большое отличие от биржевой улыбки, но если это пересчитать в пункты временной стоимости, то разница совсем незначительная.
После этого сделал простенькую модель движения улыбки: центр новой улыбки будет перемещаться по исходной улыбке. Например, если сегодня БА=120000, то модельная улыбка переместится так:
( Читать дальше )






















