Kurbakovsky
Обобщенная модель ценообразования опционов. Часть 5. Формула стоимости опциона
- 06 ноября 2019, 15:55
- |
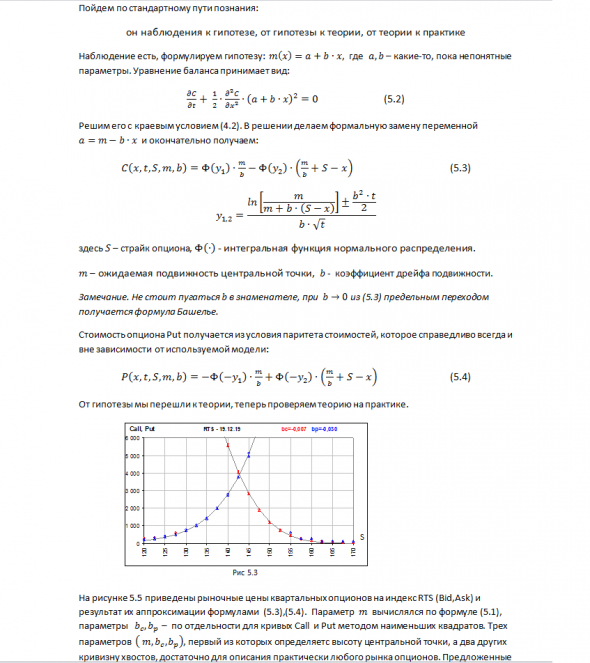
( Читать дальше )
- комментировать
- ★33
- Комментарии ( 66 )
Обобщенная модель ценообразования опционов. Часть 4. Уравнение реализации
- 29 октября 2019, 11:51
- |

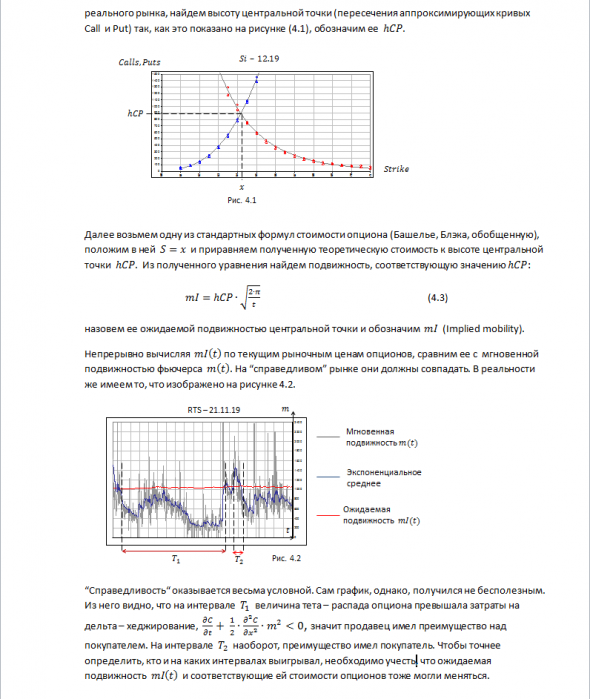
( Читать дальше )
Обобщенная модель ценообразования опционов
- 17 октября 2019, 14:39
- |
Я попробую небольшими частями изложить основные положения обобщенной теории опционов. При ее разработке не использовалась гипотеза о случайном поведении цены базового актива по причине того, что для большинства финансовых рынков ее невозможно ни подтвердить, ни опровергнуть. Обобщенная теория индифферентна по отношению к причинам ценовых изменений и в этом ее отличие от классической теории опционов, для которой гипотеза о случайном поведении цен является незыблемым основанием. Важно отметить, что в случае согласия с гипотезой классическая теория не вступает в противоречие с обобщенной, но оказывается ее составной частью. Отсюда и название “обобщенная”. Она должна понравиться тем, кто не очень хорошо разбирается в методах ТВ и МС, но хочет разобраться в опционах.
Постараюсь обойтись минимальным количеством формул, хотя совсем без математики не получится. Поэтому, если что-то будет непонятно, спрашивайте.
Размещать новые части я буду с частотой примерно раз в неделю, по мере их написания. Всего частей будет, наверное, четыре или пять.
( Читать дальше )
О вычислении дельты опциона
- 09 марта 2019, 23:24
- |
О вычислении дельты опциона
Дискуссии о правильных и неправильных методах вычисления дельты опциона. Дошел до темы «Липкая денежность» против «липкого страйка».
Больше всего смущает то, что в работе Блэка и Шолеса, на которую постоянно ссылаются оппоненты, нет вообще никаких упоминаний о «кривой волатильности», волатильность у БШ есть константа. Чем «кривее» кривая IV для конкретного рынка, тем меньше модель БШ подходит для его описания, это вся информация, которую кривая IV в себе содержит.
Спор о том, следует ли учитывать ее наклон при вычислении дельты, подобен спору о количестве чертей, способных уместиться на острие иголки. Мне кажется, правильнее изменить модель БШ, чем стараться подогнать ее неверные результаты под реальные рынки.
Напомню об одном из возможных подходов к такой модификации.
1. Собираем статистику — набор исторических пар {d(Fut),d(ImpVol)};
Где d(Fut) – дневное приращение БА
d(ImpVol) – приращение волатильности опционов на центральном страйке за тот же день.
( Читать дальше )
Все, что не разоряет, делает нас умнее.
- 25 февраля 2019, 18:53
- |
Все, что не разоряет, делает нас умнее.
Пришло время думать о душе и делиться опытом с молодежью. Теория интересна не всем (у каждого опционщика есть своя теория опционов), поэтому буду делиться жизненным опытом. А точнее, самыми эпическими из своих торговых фейлов. Вообще-то я не верю в то, что чужие ошибки могут чему-то научить. Но, вдруг научат.
Часть 1. СМЕ. Первый американский блин.
После краха Российского рынка в конце 90-х годов все наши усилия были сосредоточены на опционах CME. Классическая теория не казалась сложной ни мне, ни Сержу, моему тогдашнему компаньону. Все было предельно понятно и до начала реальной торговли нам оставалось решить только один принципиальный вопрос – нужно ли хеджировать опционы базовым активом? Метод Монте-Карло вроде бы убеждал в том, что это не обязательно — просадки счета вполне компенсировались экономией на комиссии. Наконец решили, что хеджироваться не будем.
( Читать дальше )
Комментарий к комментариям
- 05 декабря 2018, 14:31
- |
Читаю комментарии к своим вчерашним сообщениям и не знаю уже, как реагировать. Вот пример:
“Если что-то выглядит как СВ, ведет себя как СВ и не содержит в себе обнаружимых закономерностей, то почему мы должны отказывать себе в удовольствии использовать наработки из теорвера и матстатистики?”
Смысл моих постов в обратном:
“Если что-то выглядит как СВ, ведет себя как СВ”, но на самом деле СВ не является, то “использование наработок из теорвера и матстатистики” ведет к проигрышу!
Излагать проще я не умею.
Но попробую
Вы наблюдаете за автомобилем, движущимся по Варшавскому шоссе в направлении области. После двух часов наблюдений по оценкам скорости и направления делаете статистически значимый вывод о том, что через трое суток автомобиль окажется в окрестности Варшавы. В районе Обнинска автомобиль останавливается, водитель забирает с дачи тещу и едет обратно в Москву. В чем ошибка? С точки зрения статистики все безупречно. Ошибка в предположении о случайном характере процесса.
( Читать дальше )
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов. Вопросы 3,4.
- 04 декабря 2018, 16:30
- |
3. Оправдано ли использование логарифмического нормального распределения для описания терминального состояния базового актива
Можно догадаться, почему именно логнормальную модель распределения использовали Блэк и Шолес при решении задачи о нахождении справедливой стоимости опциона. Модель с гауссовыми приращениями брать было нельзя – она допускает уход цены БА в отрицательную область. Следующая, относительно простая логнормальная модель вполне годилась. Найденное на ее основе решение стало основой всей современной теории опционов.
Теперь ложка дегтя.
Мы предполагаем, что приращения цен акций, входящих в расчет индекса РТС, независимы и подчинены закону логарифмического нормального распределения. Поэтому при вычислении цен опционов на эти акции мы используем формулы БШ.
Но, согласно Центральной предельной теореме, из этого же предположения следует и то, что распределение приращений их линейной комбинации (то есть самого индекса РТС) должно быть близким к нормальному, тогда для расчета стоимости опционов на индекс РТС правильнее использовать формулу Башелье. Тем не менее, мы используем формулу БШ. Видимо, в расчете на то, что кривая волатильности все исправит.
( Читать дальше )
Несколько неудобных вопросов, касающихся методов расчета справедливой стоимости опционов. Второй вопрос.
- 04 декабря 2018, 16:11
- |
- 1. Что такое кривая волатильности и как она соотносится с моделью БШ
Все знают, что такое ожидаемая волатильность опциона (Implied Volatility). Это волатильность, которую нужно подставить в формулу Блэка-Шолеса, чтобы получить текущую рыночную стоимость опциона. Вычислив ее для всех страйков, можно затем аппроксимировать полученные значения гладкой параметрической кривой – кривой волатильности.
Но, если при расчете кривой волатильности мы всегда и везде используем формулу БШ, то мы так же всегда и везде должны доверять ее авторам, а они утверждали, что волатильность опционов должна в точности равняться волатильности базового актива, которая может быть только одна. Откуда взялась кривая? Либо мы верим Блэку и Шолесу (должна быть прямая), либо не верим (тогда кривая).
У кривой волатильности нет содержательного смысла. Это простая подгонка. Единственным ее назначением является устранение расхождений между теоретическими и рыночными ценами. Какую бы модель ценообразования опционов мы ни взяли, кривая волатильности исправит все ее огрехи. Что-то вроде толстого слоя штукатурки, с помощью которого можно выровнять любую стену.
При этом мы полностью лишены возможности отличить хорошую модель от плохой, после использования кривой расчетные цены любой модели будут близки к рыночным. Тогда почему мы пользуемся именно моделью БШ? Видимо, потому, что де-факто она признана стандартной.