Избранное трейдера tashik
How much is the опцион?
- 29 июля 2016, 12:21
- |
Представим очень простую (скажем прямо — примитивную) модель изменения цены акции. Каждый день цена акции может измениться только на 1 рубль, вверх или вниз. Вот так:

И мы хотим купить опцион колл с ценой исполнения (страйком) 100. Как понять, сколько нам платить продавцу, чтобы цена была «справедливой»?
1. Максимальная прибыль в этой модели (которая на картинке) — 6 рублей. Дороже 5.99 рублей покупать смысла точно нет.
2. За 0 рублей нам его тоже не продадут.
( Читать дальше )
- комментировать
- ★48
- Комментарии ( 26 )
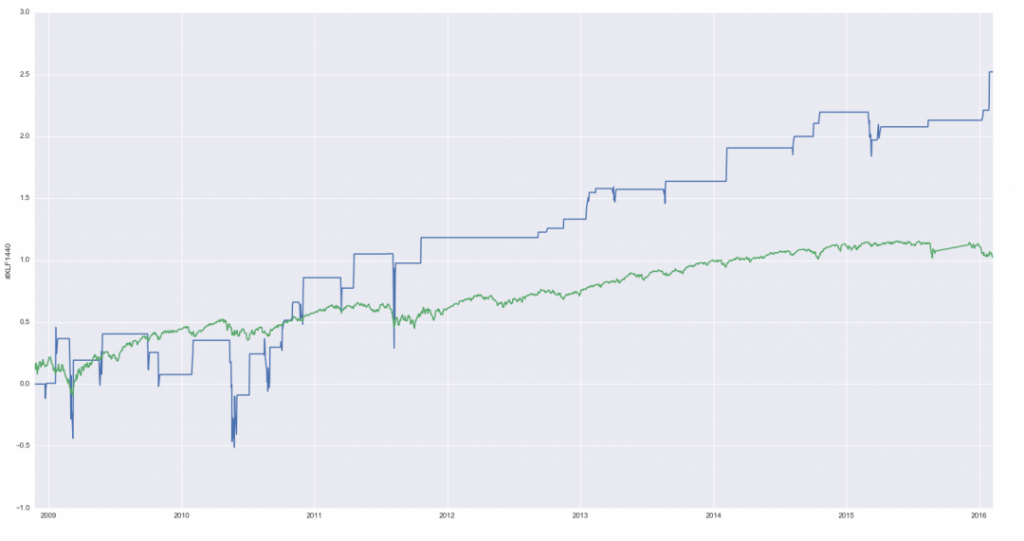
Предсказание чего угодно с использованием Python
- 22 мая 2016, 12:43
- |
Небольшая статья с ресурса http://www.talaikis.com/ о построении простой стратегии, использующую наивный байесовский классификатор при создании процесса возврата к среднему. Весь код в статье приведен на языке Python.
Это достаточно большая область исследований, но расскажем все очень кратко. Мы попытаемся найти взаимоотношение между временными сериями (в данном случае возьмем в качестве сигнала взаимный фонд XLF из финансового сектора, сдвинутый по времени на 1 день назад), а нашей целью будет фьючерс S&P500 в форме CFD. Будем входить в длинную позицию по этой бумаге при нулевой вероятности приращения. Логически нулевая вероятность ни о чем не говорит, другими словами, будем покупать возврат к среднему.
1. Получение данных
Y = read_mongo(dbase, "S&P5001440") X = read_mongo(dbase, syms[s]).shift() #готовим набор данных res = pd.concat([X.CLOSE, Y.CLOSE], axis=1, join_axes=[X.index]).pct_change().dropna() res.columns = ['X', 'Y']
( Читать дальше )
Мои статьи про R, машинное обучение, количественный анализ
- 07 мая 2016, 05:45
- |
- Мои шаги в сторону машинного обучения на R и немного про Si, Brent
- Расчет ожидаемого количества убыточных сделок подряд на R
- Применение логарифмов для расчетов со сложным процентом
- Построение модели для парной торговли акциями Google и Apple на R
- Анализ Brent с использованием языка R
- Количественный анализ графика нефти с применением R (продолжение)
- Гистограммы доходностей разных активов
- Применение наивного байесовского классификатора на R для поиска закономерностей и прогнозирования
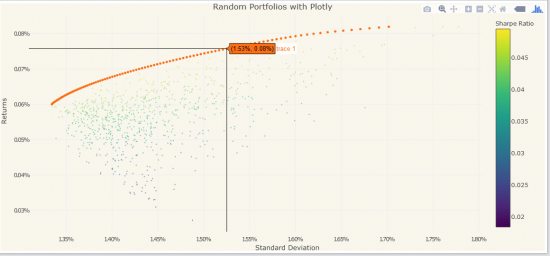
Оптимизация портфеля на R
- 29 апреля 2016, 12:52
- |
И так задача: Есть следующий набор инструментов «GAZP», «ROSN», «LKOH», «TATN», «NVTK», «SNGS», «BANE», построить на их основе оптимальный с точки зрения риск/доходность портфель. Задачу не станем усложнять такими введениями как использование плечей, ограничение по капиталу на бумагу итд. как это все делается можно подробно прочесть в описании фреймворка. Решим лишь что минимальная допустимая доля инструмента в портфеле 5% максимальная 80%
Эффективная граница портфеля
( Читать дальше )
Бесплатная тиковая база данных (CME)
- 15 февраля 2016, 18:22
- |
Всем привет.
Решил выложить в открытый доступ базу данных тиков с CME, которая накапливалась за последние годы, и обновляется по итогу дня.
FTP доступ:
85.25.211.62
login: smartlab
pass: smartlabpass
Ссылки на торрент: http://ge.tt/1Ql8j3Y2
№2: app.box.com/s/h0dhmkif0fhnvlpzdp8ma89c1ysv876t
Формат данных:
seconds (int32) — кол-во секунд с начала суток по Чикаго.
milliseconds (int32)
price (int32)
volume (int32)
bestBidPrice (sbyte) — расстояние в тиках между price и реальной ценой BidPrice
bestAskPrice (sbyte) - расстояние в тиках между price и реальной ценой AskPrice
bestBidSize (int32) — доступно с июня 2015
bestAskSize (int32) - доступно с июня 2015
Ниже код для чтения бинарных файлов (На C#).
Создаем класс Tick:
- public class Tick
- {
- public DateTime Time { get; set; }
- public int Price { get; set; }
- public int Volume { get; set; }
- public int BidPrice { get; set; }
- public int AskPrice { get; set; }
( Читать дальше )
Варианты прямого доступа к Московской Бирже
- 11 февраля 2016, 20:26
- |
На колокации в зоне биржи доступны:
1.Валютный рынок и Рынок Акции/Облигации
FAST — протокол мультикаст раздачи рыночных данных.
FIX - протокол для постановки заявок.
ASTS Bridge он же Teap - забудьте о его существовании.
Волшебные буквы ASTS подразумевают подключение любым из вариантов -)))
2. Рынок FORTS
CGate — уникальная утилитка в виде черного окошка.(Здесь следует добавить заклинание Plaza II ). Позволяет получать два вида биржевых данных.
Без ордер лога — урезаный режим в котором поступают данные по стаканам.
Полный ордер лог - режим в котором приходит лог всех заявок (поставленных снятых исполненных и т.д.)
( Читать дальше )
Философия трейдинга (опционного) в картинке
- 18 января 2016, 22:22
- |

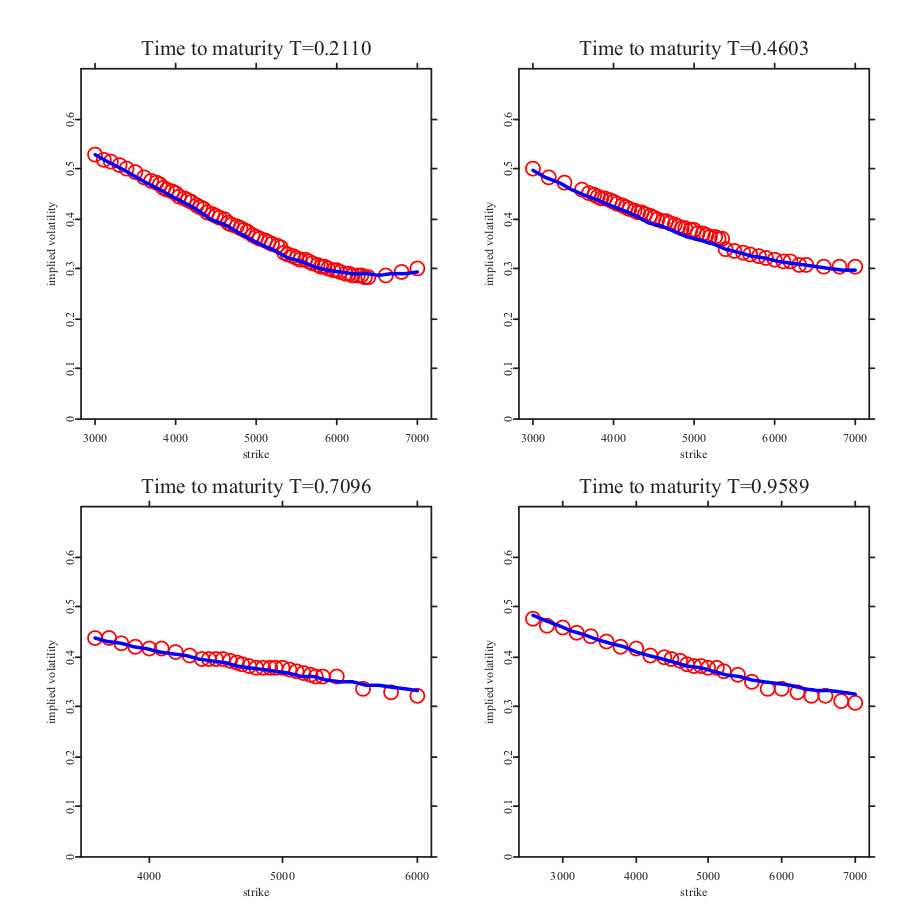
Улыбка волатильности. Модель Бейтса
- 07 мая 2015, 10:15
- |
Продолжение. Начало в моем блоге и на сайте.
В прошлой статье про модель Хестона мы отметили, что она обладет недостатком, который проявляется в неточности определения цен опционов на малых сроках экспирации. Здесь мы рассмотрим модель Бейтса, в которой этот недостаток устранен, и она является одной из лучших аппроксимаций, описывающих поведение цен опционов для разных страйков и периодов до экспирации.
Модель Бейтса относится к моделям стохастической волатильности и определятся следующими уравнениями:
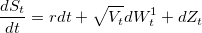
( Читать дальше )
Парный трейдинг опционами.
- 06 марта 2015, 14:38
- |
Метод торговли прекрасно работает до резкой раздвижки спреда, которая рано или поздно происходит, если бы не раздвижка — был бы грааль 100%.
Как же избавиться от недостатков данного метода, сохранив все его достоинства, при этом главный недостаток (раздвижка спреда) сделать самой большой возможностью заработать?
Все просто, нужно применить навыки парного трейдинга на опционах!
Берем разные страйки одного б/а и, создаем график спреда между страйками, создаем 2 позиции как на картинках ниже, и спокойно торгуем спред откусывая понемногу профита и с нетерпением ждем резкой раздвижки спреда которая нам позволит как минимум заработать десятки процентов к депозиту!
То есть что мы имеем в итоге: при флете б/а мы зарабатываем по немногу на спреде (главное не теряем), при резком движении б/а мы очень хорошо зарабатываем, позицию лучше делать максимально дельта и тетта нетральной.
( Читать дальше )
Весь Гном в одном месте.
- 13 июля 2014, 22:36
- |
Гном. Или как трейдер обанкротил банк.
Глава первая и вторая
Глава третья и четвертая
Глава пятая и шестая
Гном 2. Возвращение.
Глава первая
Глава вторая и третья
Глава четвертая и пятая
Глава шестая и седьмая
Глава восьмая и девятая
Глава десятая, одиннадцатая и двенадцатая.
Просто про опционы.
Вместо предисловия
Глава первая
Глава вторая
Глава третья
Глава 3 1/2
Глава четвертая
Глава пятая
Глава 5 1/2
Глава шестая
Глава седьмая
Не окончена...
История одного робота
Глава первая
Глава вторая
Глава третья
Глава четвертая
Глава 4 1/2 и пятая
Глава шестая
- bitcoin
- brent
- eurusd
- forex
- gbpusd
- gold
- imoex
- ipo
- nasdaq
- nyse
- rts
- s&p500
- si
- usdrub
- wti
- акции
- алготрейдинг
- алроса
- аналитика
- аэрофлот
- банки
- биржа
- биткоин
- брокеры
- валюта
- вдо
- волновой анализ
- волны эллиотта
- вопрос
- втб
- газ
- газпром
- гмк норникель
- дивиденды
- доллар
- доллар рубль
- евро
- золото
- инвестиции
- индекс мб
- инфляция
- китай
- кризис
- криптовалюта
- лукойл
- магнит
- ммвб
- мобильный пост
- мосбиржа
- московская биржа
- мтс
- натуральный газ
- нефть
- новатэк
- новости
- обзор рынка
- облигации
- опрос
- опционы
- отчеты мсфо
- офз
- оффтоп
- прогноз
- прогноз по акциям
- путин
- раскрытие информации
- ри
- роснефть
- россия
- ртс
- рубль
- рынки
- рынок
- санкции
- сбер
- сбербанк
- северсталь
- сигналы
- смартлаб
- сущфакты
- сша
- технический анализ
- торговля
- торговые роботы
- торговые сигналы
- трамп
- трейдинг
- украина
- фондовый рынок
- форекс
- фрс
- фьючерс
- фьючерс mix
- фьючерс ртс
- фьючерсы
- цб
- цб рф
- экономика
- юмор
- яндекс


















 Новости тг-канал
Новости тг-канал